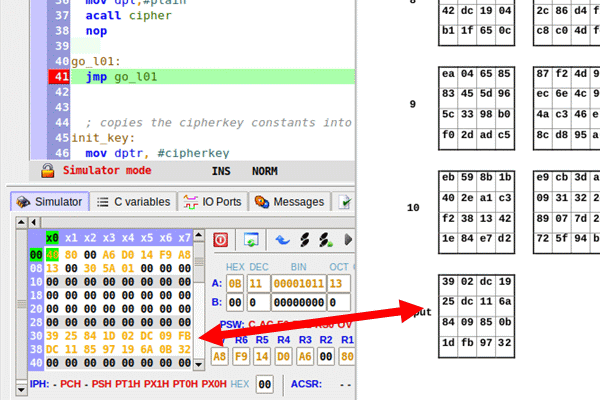
Picture 0: Code successful execution in the MCU 8051 IDE Simulator
Introduction
This article describes my implementation of the AES-128 encryption algorithm, using the assembly language of the 8051 microcontroller.
Background
Recently (don't ask me why), I became interested in the 8051 microcontroller.
As you probably already know, the 8051 is a CISC, 8 bit MCU, with scarce memory resources (128 bytes of internal RAM! See the dedicated Wikipedia page[^] for details).
I implemented the AES-128 cipher algorithm in order to get acquainted with its instruction set and 'feel the thrill' of the CISC (I am used to RISC devices).
The following documents were my background and could be as well yours.
This is the AES algorithm description. It is very very (very!) well written: I suggest everyone have a look at this fine piece of documentation.
This is 'The Reference' for programming with 8051 assembly. You may find its PDF available on the web (I don't provide a link, because I was not able to find its official repository).
- FIPS 197, Advanced Encryption Standard (AES) - NIST Page
- (Intel) MCS@51 MICROCONTROLLER FAMILY USER’S MANUAL
Additionally, I have used the MCU 8051 IDE (see MCU 8051 IDE - Wikipedia[^]) for editing, compiling (that is, produce machine code from assembly one) and running the code (via the included simulator).
Again, such IDE is a fine piece of software (hats off to Martin Ošmera). It runs only on Linux OS, though. I strongly encourage Windows users to get their hands on a Linux box (e.g., a virtual machine) in order to use it.
Using the Code
You have to use the cipher routine, which takes just an argument, the address of the plain text (16 bytes) array in the dpl register, while the encryption key is hard coded in flash memory (of course, you may change such a behaviour).
The routine produces its output in-place (that is replacing the content of the plain text array with the corresponding ciphered one.
The provided project (as shown in picture 0) uses the same input (and key) used in the NIST document's "Appendix B – Cipher Example", producing, fortunately, the same output.
Implementation Details
The Pseudo Code
The starting point for the implementation is the pseudo code provided by the NIST document [1], specialized for AES-128 and slightly rearranged:
KeyExpansion(byte key[16], word w[44])
//...
end
Cipher(byte in[16], byte out[16], word w[44])
begin
byte state[4,4]
state = in
AddRoundKey(state, w[0, 3])
for round = 1 step 1 to 10
SubBytes(state)
ShiftRows(state)
if round < 10 then
MixColumns(state)
end if
AddRoundKey(state, w[round*4, round*4 +3])
end for
out = state
end
Code 0: The original algorithm pseudo-code
Unfortunately, such a pseudo code cannot be directly implemented on the 8051 mcu, due to the expanded key memory requirements (w[44] array, 176 bytes long, see section 5.2: "Key Expansion" in [1]).
To overcome the obstacle, the key expansion step is performed round by round directly in the Cipher code: the 'round' key is computed using the previous round one.
This way, memory requirements for key expansion reduce to 32 bytes.
The modified pseudo code follows:
byte prevkey[16]
byte roundkey[16]
InitKey()
// initialize roundkey with key
// ..
end
NextKey(byte round)
// computes roundkey using prevkey and round variable
// ..
end
Cipher(byte in[16])
begin
InitKey()
AddRoundKey(in, roundkey)
for round = 1 step 1 to 10
SubBytes(in)
ShiftRows(in)
if round < 10 then
MixColumns(in)
end if
NextKey(round)
AddRoundKey(in, roundkey)
end for
end
Code 1: The 'modified' pseudo code
Where:
- The
InitKey and NextKey couple of routines replace the KeyExpansion step. - Cipher happens in place (
state and out variables removed). - Explicit dependence on external
roundkey and prevkey (used by NextKey) arrays is shown.
The Actual 8051 Assembly Code
The code is composed of:
- the constant tables
- the reserved RAM
- the XTIME macro
- the main routine (cipher)
- the subroutines
Every component is detailed below.
The Constant Tables
The algorithm requires some tables of constants, namely sbox and rcon.
Additionally, the plain text block and the user provided encryption key arrays need to be stored in persistent memory, in order to provide at least the initialization code for the corresponding RAM variables.
To summarize, we have:
| array | size (bytes) | notes |
sbox | 256 | The substitution matrix, see "5.1.1 SubBytes()Transformation" of document [1] |
rcon | 11 | The round constants, required by the Key Expansion steps, see "5.2 Key Expansion" of [1] |
input | 16 | The algorithm input data (plain text) |
cipherkey | 16 | The user provided 128-bit encryption key |
Table 1: The constant arrays stored in flash memory
Note: I've used the term 'array' instead of 'table' in order to describe the constants. This reflects more the implementation point of view: 'columns' and 'row' operations of the original algorithms are flattened into their arrays equivalents in the code (code comments refer to the original algorithm terminology).
All the arrays are automatically generated from the corresponding ones found in available C implementations.
The values are stored in flash memory using the db assembly directive (see the MCU 51 IDE documentation for details), as shown in the following figure:

Picture 1: Constant table definitions in the MCU 8051 IDE
The Reserved RAM
Some of the mcu internal RAM is used by the algorithm implementation, namely:
All the available 8051 general purpose registers (r0,..,r7, a, ...) but dpl (which is preserved).
The following memory chunks:
16 bytes, starting at 0x70 to store current round key16 bytes, starting at 0x60 to store the previous round key1 byte, at address 0x5F to hold current round number
This way, a fairly large amount of RAM (63 bytes!) remains available to the algorithm consumer.
The stack is used both implicitly, for storing return address in subroutine calls, and explicitly (via push/pop instructions) for preserving the dpl register value.
The XTIME Macro
The XTIME implements the algorithm xtime operation, that is the multiplication by x in the Galois field GN(2^8) (see: "4.2.1 Multiplication by x" of [1]).
The macro is used many (8) times by the mix_columns subroutine.
It resolves to a left-shift and a conditional XOR with 0x1B (if its operand original value had bit 7 set):

Picture 2: The XTIME assembly macro
(There is a white lie in Picture 2, you may see the actual macro definition in the provided source code.)
Note
- The Register
a is used both as argument and result. - Since the
8051 mcu doesn't provide a shift instruction,
add a, a
was used instead. It sets the carry if a register original value has bit 7 set, hence the code skips the XOR on 'carry clear' condition. - A macro is used instead of a subroutine because the call/return overhead would be expensive on such a small amount of code.
The Main Routine (Cipher)
Conceptually, the cipher routine follows accurately the 'modified' pseudo code (Code 1) and the implementation reflects it, so it resolves to various calls to the accessory routines, like for instance:

Picture 3: Sample subroutine call in the cipher code
Both in its startup code and inside the loop over the various rounds.
The AddRoundKey and SubBytes operations are the exceptions: There is no subroutine for them, their code is directly included inside the cipher routine.
In the following figure, the SubBytes code is reported, as an example of access to flash memory constants.

Picture 4: The assembly code corresponding to SubBytes operation
Namely, the 'substitution value' rcon[state[k]] is obtained:
- moving
state[k] in the register a - moving the address of
rcon in the dptr register - using the
movc instruction for moving the value at flash address (a+dptr) into register a
The Subroutines
The accessory routines are:
init_keynext_keyshift_rowsmix_columns
The init_key Subroutine
The init_key subroutine simply copies the user provided key (cipherkey in flash memory) into the roundkey array, so there is not much to write about.
The next_key Subroutine
The next_key subroutine is more elaborate. It must produce the key for the next round of encryption, using, as input, the current round key and the number of the next round.
It starts copying the content of the rndkey array into the prvkey.
Then it initializes the temporary variable temp (i.e., the r4,..r7 registers) and starts the computation of w4[nround*4] faithfully following the operations described in [1], namely:
temp = rotw(w3)
temp = subword(temp)
temp ^= rcon[nround]
w[nround*4] = temp ^ w[(nround-1)*4]
Code 2: Steps used in order to compute w4[round*4]
Afterwards, it computes the other (simpler) values.
w[nround*4+1] = w[nround*4] ^ w[(nround-1)*4+1]
w[nround*4+2] = w[nround*4+1] ^ w[(nround-1)*4+2]
w[nround*4+3] = w[nround*4+2] ^ w[(nround-1)*4+3]
Code 3: Other components of the next key are much simpler to obtain
You might easily follow the above steps in the next_key source code, since they are all commented.
For instance:
![The temp ^= rcon[nround] step](data:image/gif;base64,R0lGODlhAQABAAAAACH5BAEKAAEALAAAAAABAAEAAAICTAEAOw==)
Picture 5: The temp ^= rcon[nround] step
The shift_rows Subroutine
This is a straightforward implementation of document [1] "5.1.2 ShiftRows() Transformation". Again, you may follow it, thanks to the comments. The tricky points, in my opinion were:
- keeping track of current row and column indices
- taking care of clearing the carry flag before using the
subb instruction
The mix_columns Subroutine
This is also a straightforward implementation of the corresponding operation described in document [1] ("5.1.3 MixColumns() Transformation")
It starts copying the column components into the temporary variables (r4,..r7) and then applies the steps described in [1], namely linear combinations of the column components themselves via the addition operator (XOR) and the multiplication one (xtime).

Picture 6: An excerpt of the mix_columns subroutine
init_key and next_key realize the KeyExpansion operation incrementally, in a round-wise manner while shift_rows and mix_columns provide the functionalities described, respectively in "5.1.2 ShiftRows() Transformation" and "5.1.3 MixColumns() Transformation of the document [1].
Points of Interest
Disclaimer
This is my first 8051 assembly program, the code is not fully tested against the NIST vectors. It is a seemingly successful experiment, nothing more. If you intend to use it, then I strongly suggest to fully test it against the vectors.
Things Learned
Implementing the AES-128 on the 8051 had a two folded effect:
- Made me appreciate the
AES encryption algorithm in its details - Made me get well acquainted with the
8051 instruction set and architecture
Some Numbers
Code memory usage, about 16%
The full cipher code (constant tables includes) is 668 bytes long (the flash is 4096 bytes long).
Internal RAM usage, about 38% (excluding the stack)
The implementations uses 49 bytes for incremental key expansion and temporary variables.
Execution time: 14.162 ms (according to the simulator)
That corresponds roughly to 10^4 instructions for the encryption of a 16 bytes block (this is apparently the weak side of this implementation).
What to do next?
The decipher implementation, of course.
History
- 11th November, 2019 - First release
