Introduction
Computers calculate numbers in binary. We forget about this many times as the illusion of a mathematical machine is quite compelling. It’s far easier to forget about binary rounding errors and pretend that calculations are precise.
Alas! This doesn’t add up for dull purposes like accounting and bookkeeping. Here, a roundoff error of 1 cent can sent an accountant screaming for an explanation and a multi-million dollar investigation. And it is for accounting reasons that databases have special datatypes like NUMERIC and DECIMAL that are precise number formats. This is in contrast with approximate data types like FLOAT and REAL.
In the C++ language, the built-in datatype “double” (IEEE 754) datatype is in radix 2, so it is also an approximate datatype. Although the Intel x386 processor has something of a ‘bcd’ type of operator to correct the effect of binary calculations, no C++ compiler today exists with a built-in exact numeric datatype. (Borland C++ 2.0 being the last one that had that!)
The solution has been to store these numbers in the so-called “BINARY-CODED-DECIMAL” format. BCD for short. In such an implementation, no rounding errors can occur, as extra bits are used to represent a decimal number instead of a binary number.
This lack of a binary-coded-decimal datatype makes it cumbersome to do accounting and bookkeeping calculations in C++. Also, the storing and retrieving of NUMERIC and DECIMAL numbers to and from databases require lengthy calculations to convert the numbers, requiring precious CPU cycles.
The ODBC Case
The ODBC (Open-DataBase Connectivity) standard has a data structure (SQL_NUMERIC_STRUCT) to transport the data for NUMERIC and DECIMAL numbers. Data for these datatypes is often binded and used in ODBC applications as a string. The binary transport of that data in a radix 256 numeric struct is often too great a challenge for most programmers on a daily business schedule.
The chapter about “BCD and the ODBC Standard” explains how this bcd class solves that problem.
Predecessors of BCD
There have existed (and still exist!) a number of predecessors to this bcd class.
4GL Programming Languages
Fourth generation languages bonded to a specific database platform (e.g., INFORMIX-4GL) had a DECIMAL datatype as a built-in feature. Binary coded decimal calculations were the default on this platform which made it typically suited to build accounting software and store the results in a database.
The Borland C++ Compiler
Upto the point where Borland sold their C++ compiler to Embarcadero, it had a built in ‘bcd’ datatype that could be directly used, just as you would use an ‘int’ or a ‘double’. To my best knowledge, this datatype was dropped in the later versions of this compiler.
Microsoft has never bundled a ‘bcd’ datatype with their implementation of the C++ language. And the language itself, not even through the process of the ISO standard, has ever featured such a datatype. So Borland was unique in this respect.
Integer-coded-decimal
In order to do exact numerical calculations, my first try was to implement a numeric class that stores the numbers in integer format. 4 integers before the decimal point and 4 integers after the decimal point. This implementation – dubbed the integer-coded-decimal – did allow for 16 decimal places before and after the decimal point. Enough to do the bookkeeping of a large multi-national company or a small country. 😊
Although the classical operators like adding and subtracting are easy to implement in this format, much was left to be desired. As soon as we want to implement more mathematical operators, this implementation becomes bothersome, and as we will see later: slow.
Arbitrary-Floating-Point
After some searching in the mathematical realm, I found the arbitrary-floating-point (AFP) class of Henrik Vestermark. This library takes the approach of storing the mathematical mantissa and the fractional part separately. The fractional part is stored in a character array, and interpreted in each mathematical operation. As such, it is an implementation of a precise binary-coded-decimal.
The source code of this library is included in the BCD project. But see also the website of “Numerical Methods at Work” at http://hvks.com as this project has evolved since I took the idea from it.
The downside of this library is (apart from performance problems) that the format is not easily transcoded to database formats like NUMERIC and DECIMAL.
The Best of Both Worlds
Both methods (integer-coded-decimal and arbitrary-floating-point) have led the resulting design of the binary-coded-decimal class here presented. It stores the exponent and the mantissa separately. The mantissa however is stored as a set of integers. In the current configuration, 5 integers for 8 decimal positions each is used. Thus allowing for a mantissa of 40 positions. More than enough to even handle the most demanding database implementation (Oracle with 38 positions).
Integers can hold at least 9 decimal places as a positive 32-bit “int” or “long” can hold up to the number of 2.147.483.647. This makes it possible to hold 8 decimal places and still have one digit left to hold any carry or borrow number when iterating over and array of these integers.
The BCD Datatype
The BCD (Binary-Coded-Decimal) datatype was built with database numeric and decimal datatypes in mind. A binary-coded-decimal number is an EXACT number with no rounding errors due to the binary nature of a computer CPU (Central Processing Unit). This makes the bcd datatype especially suited for financial and bookkeeping purposes.
BCD calculations have been present in computer science for quite some time, and in various forms. This BCD class was especially designed to co-exist with ODBC database adapters. For more information, see the chapter “BCD and the ODBC Standard”.
Construction and Initialization
You can construct a bcd from just about every base C++ datatype, while initializing the bcd at the same time. This goes for chars, integers, longs, 64bit-integers, floats and doubles.
bcd num1(2);
bcd num2(4.0);
bcd num3 = num1 + num2;
But also for strings and from other bcd number.
bcd num4("7.25");
bcd num5(num3);
bcd num6 = num4 + num5;
Here is a complete list of all constructor types:
- The default constructor (initializes the number to zero (‘0.0’))
- Constructed from a char number (-127 to +127)
- Constructed from an unsigned char number (0 upto 255)
- Constructed from a short (-32767 upto 32767)
- Constructed from an unsigned short (0 upto 65535)
- Constructed from an integer (-2147483647 upto 2147483647)
- Constructed from an unsigned integer (0 upto 4294967295)
- Constructed from a 64bits integer (-9223372036854775807 upto 9223372036854775807)
- Constructed from an unsigned 64bits integer (0 upto 18446744073709551615)
- Constructed from another bcd
- Constructed from a
string of type CString (MFC) - Constructed from a
string of type “const char *” - Constructed from a
SQL_NUMERIC_STRUCT (as appearing in the ODBC standard)
Constants
There are three defined constants in the bcd datatype. These constants are:
PI: The well known circle/radius ratioLN2: The natural logarithm of 2LN10: The logarithm of 10
They appear as “const bcd” numbers and can be used as such. Here are a few simple examples to show their use.
bcd ratio = 2 * PI();
bcd quart = bcd::PI() / bcd(2);
Assignments
Other bcds, integers, doubles and strings can be assigned to a bcd number. That is: you can use the standard ‘=’ assignment operator or the operators that are combined with the standard mathematical operations ‘+=’, ‘-=’, ‘*=’, ‘/=’ and ‘%=’. Assignment operators made of a combination with bitwise operators like ‘|=’ or ‘&=’ have no logical counterpart in the bcd class, as a bitwise operation has no logical meaning for a binary coded decimal number.
bcd a = SomeFunc();
a += 2;
a *= b;
Increments and Decrements
Both prefix and postfix increments and decrements can be used with a bcd just as with any integer number.
bcd a = ++b;
bcd c = a--;
Operators
The standard mathematical operators ‘+’ (addition), ‘-‘ (subtraction), ‘*’ (multiplication), ‘/’ (division) and ‘%’ (modulo) are implemented for the bcd class.
As this class is designed to do bookkeeping, it is the ‘bread-and-butter’ of this class. More than eighty percent of all calculations are done in these operators in real-world applications.
Here is a typical example:
bcd total;
for(auto& obj : objectlist)
{
total += obj.GetPrice() + obj.GetVAT();
}
bcd average = total / (int)objectlist.count();
if(average > 400.0)
{
ReportAverageToHigh(average);
}
Comparisons
All typical comparison operators like equal (==), not-equal (!=), smaller (<), smaller-than-or-equal-to (<=), greater (>) and greater-than-or-equal-to (>=) are implemented for the bcd class.
For an example, see the previous paragraph where we report an average that is too high.
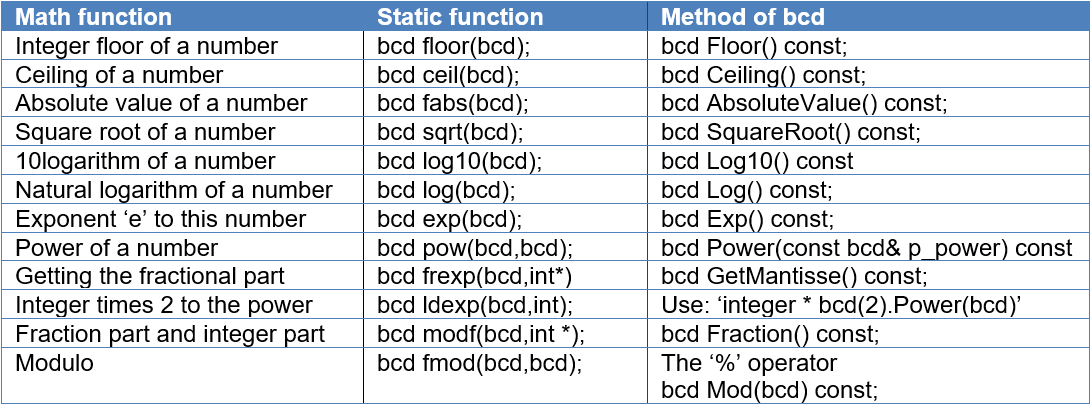
Mathematical Functions
The C library contains a number of mathematical functions that are solely implemented in the ‘double’ basic datatype. An example of these is, e.g., “pow” for the taking of a power. These functions are implemented as statistical functions with bcds as parameters. Static mathematical functions include:
Apart from the static functions, they are also implemented as methods of the bcd class. So “pow” has a symmetrical method ‘Power’.
Here are two examples that do exactly the same:
bcd surface = GetSquareSurfaceArea();
bcd side = surface.SquareRoot();
and:
bcd surface = GetSquareSurfaceArea();
bcd side = sqrt(surface);
NOTE: Overloading the mathematical functions make is meant to make it easier to port existing code with doubles to be converted into bcds.
Trigonometric Functions
The standard C trigonometric functions are overloaded for the bcd class as is the case with the standard mathematical functions. Just as with the standard trigonometric functions, the number is an angle measured in radians. The following functions exist:

Here are two examples that do exactly the same:
bcd waveHeight = GetSignal().Sine();
and:
bcd waveHeight = sin(GetSignal());
Conversions
It is possible to convert a bcd to ‘something-else’. This other ‘something’ is a base datatype from the C++ language. Most methods are named something like “AsXXXX”, where XXXX denotes the type we want. The following methods exist:

Here is an example of a calculation returning an engineering number string in 10 exponential format.
CString GetCalculation()
{
bcd number1 = SomeFunction();
bcd number2 = AnotherFunction();
bcd number3 = number1.Power(number2);
return number3.AsString(Engineering,false);
}
String Display
Numbers can be displayed as strings. How they are displayed depends on the application we are using the number in. This can be quite different for a scientific or engineering application in contrast to a bookkeeping application. The differences are loosely defined as:
- n bookkeeping applications, we tend to display numbers with one decimal marker and as much thousand parts markers as needed. We display decimal places upto a defined amount and round of the rest of the decimal places;
- In engineering applications, we tend to print the exact number just with one decimal marker. If the number gets to great (or to small) we shift to exponential display in powers of ten.
- In both cases, we always print a negative number with a negative sign (-), but we can choose to print the positive sign (+) as well;
- The decimal and thousand markers are defined by the current system local of the machine and thus the language the desktop is currently using.
Here are a few examples of both ways of displaying a number:

File Reading and Writing
Applications might need to write information to a binary file. So there are two methods for integration with binary files. The first (WriteToFile(FILE*)) writes the bcd number to a file. The second (ReadFromFile(FILE*)) reads the bcd number back from that file. All primary factual information of the bcd number is stored.
Any disturbance in the force (oh sorry: the file) will lead to an error, meaning the whole number gets stored or read back, or an error occurs. See the implementation for more details about the storing format of the bcd.
Storage and retrieval of the bcd number in the file is also network independent and little-big-endian independent, meaning you can store and retrieve the number in a portable way.
Information and Other Methods
A number of methods exist that have not yet been discussed. The give information of some property of the bcd number or do a basic operation. Here is the remainder list:

Error Handling
Error handling is done by throwing a StdException. This exception is integrated with the MS-Windows C++ Safe Exception Handling in such a way that critical errors like null-pointer references and division-by-zero errors do **NOT** get a different exception handling – stopping the application, e.g., – but are integrated in the exception throwing.
Here is a list of all errors in the bcd class. There descriptions are meant to be self-explanatory:

Enhancements and Refinements
The bcd class can easily be enhanced. You can simply expand the number of digits in the mantissa by using a greater number on integers in the mantissa array. See the constants “bcdDigits” and “bcdLength” at the beginning of the class interface definition.
Extra methods and / or data, operators, stream interfaces like std::iostream can easily be added to this class.
The bcd project comes with a unit test module DLL. The goal of the unit test is, of course, to test the correct workings of the other functionality while you expand the class.
Just open the test explorer in Visual Studio (from the menu “Test” / “Run all tests”) and check that all unit test are ‘in-the-green’.

Now with the mathematical calculations firmly in place, we can turn to the usage of the bcd number in combination with the ODBC drivers. Binary data flows to and from the ODBC driver of a database in the form of the SQL_NUMERIC_STRUCT. This struct supports both the NUMERIC and DECIMAL datatypes of a modern ISO:9075 compliant SQL database.
Binding directly to a DECIMAL or NUMERIC column in a database query will result in the retrieval of a SQL_NUMERIC_STRUCT in memory. Changing and using that struct in an update or insert statement will use the contents of that struct and transport it to our database record.
But what happens when we get that data. Peeking at the source code of some open-source database implementations like the MySql, MariaDB, Firebird or PostgreSQL reveals that most odbc drivers just convert a string to a SQL_NUMERIC_STRUCT. At the moment that this dataclass was written, those conversions were quite complicated, long and error prone. In the last years, the situation has improved, but…
- This conversion only converts the standard number format with a decimal point. No exponential numbers can be converted.
- A lot of confusion still exists in the usage of
NUMERIC and DECIMAL. Looking up answers on the stackoverflow platform, even experienced programmers opt-in to let the database convert the data to a string and plucking that string data out of the query.
The BCD class has been designed to easily convert to and from the SQL_NUMERIC_STRUCT. With the following two methods:
bcd::SetValueNumeric(SQL_NUMERIC_STRUCT*);bcd::AsNumeric(SQL_NUMERIC_STRUCT*);
Data is directly converted to and from the ODBC bind area and to the database. These conversions are a simple iteration over the mantissa and copy of the mantissa and sign bit.
The Main Advantage
The key factor here is that we can directly use our NUMERIC and DECIMAL numbers without having them to convert first to a string and back to a format where we can begin calculations in them. Round-about the other direction: we can directly calculate and store the result in the database without having to convert everything to strings and order the database to convert it back to exactly the same data again!
SQLComponents
The main application of the bcd class lies within the SQLComponents library. This is a library around the ODBC driver. You can find this library at https://github.com/edwig/SQLComponents.
In this library, all datarows are bound to a SQLRecord object. The columns of each record in turn are bound to the SQLVariant class.
The SQLVariant class acts as a sorts of variable placeholder for all datatypes that can be obtained from a database row. And of course: one of the datatypes is the bcd class.
The SQLComponents database makes it easier to program with any given ODBC driver. It has been tested with Oracle, MS-SQLServer, MySQL, PostgreSQL, MS-Access and IBM-Informix.
The Open ODBCQuerytool
Apart from a number of business applications, the one and only killer-app that’s using the SQLComponents and bcd class is the Open ODBC-Querytool. You can find this querytool through github on: https://github.com/edwig/ODBCQueryTool and on sourceforge under the following link: https://sourceforge.net/projects/odbcquerytool/. From this last link, it has seen more than 50.000 downloads in the last years.
Performance Measuring
In order to be able to measure the performance of my implementations, I designed a test program that does any number of calculations a configurable number of times ‘n’. When setting ‘n’ to for instance a 1000 times, the length of the calculations will be great enough to be able to measure it with a high performance counter like “QueryPerformanceCounter” of the MS-Windows kernel.
The test program compares the result of each operation with the result of the MS-Windows desktop calculator “calc.exe” and shows the performance results of four implementations:
- C++ built-in “
double” - Arbitrary-floating-point
- Integer-coded-decimal
- Binary-coded-decimal
A typical output of the test program looks like:
Testing the function [log10] for a total of [1000] iterations:
Input: 98765432109876543210.123456789012345678901234567890
Type Time Value
------ ---------- ------------------------------------------------------
calc 0.000000 +19.994604968162151965673558368195
double 0.000005 +19.994604968162150
afp 0.982142 +19.99460496816215196567355836819543212297
icd 0.191501 +19.9946049681621519656735583681954349795885
bcd 0.050899 +19.9946049681621519656735583681954321229
In this example, we see the results for the “log10” function (logarithm in base 10). As we can see, the result is correct upto at least 32 decimal places for each implementation (apart from ‘double’ ☹)
A thousand iterations take 0,05 seconds in the bcd implementation: 50 microseconds each. Quite a bit longer than the 50 nanoseconds for a double calculation. But at a far greater precision!
The BCD solution in the example program runs this test by default.
This is a screenshot of the beginning of the testrun:

And here is a sample of the output at the end of the testrun:

In a test run in the mode of 1000 iterations on a modern Intel Core i7-7700K CPU with an ASUS Z270 motherboard we can now compare the timings of all mathematical functions. Here is a typical end result, shown in a table:

Conclusion
From the performance table above it’s clear that the best performance is of course the built-in double datatype. But that’s with rounding errors and all. From the other solutions (straight 8 bits BCD by the AFP solutiohn, the integer-coded-decimal and the bcd-class) the bcd is the winner in all categories of calculations but one (addition). In those cases where bcd has the highest performance it can be from a few percent upto a staggering factor of 20 or 50 times faster or even higher.
Github
This project is also to be found on: https://github.com/edwig/bcd.
History
- 19th December, 2019: First version of this article
