“The primary aim of clustering is not just to make clusters, but to make good and meaningful ones” – Analytics Vidhya (https://www.analyticsvidhya.com/).
Introduction
An optimal multi-objective clustering is one of the most popular, and, at the same time, curious supervised machine learning problems, that occurs in many fields of computer science such as data and knowledge mining, data compression, vector quantization, patterns detection and classification, Voronoi diagrams, recommender engines (RE), etc. The process of clustering analysis itself allows us to reveal various of trends and insights exhibited on the input dataset.
The cluster analysis (CA) process allows us to determine the similarities and differences between specific data, partitioning the data in such as a way that the similar data normally belongs to a specific group or cluster. For example, we can perform the clustering analysis of the data on a credit card customer to reveal what special offers should be given to a specific customer, based on the balance and loan amount criteria. In this case, all that we have to do is to partition all customers data into the number of clusters, and, then give the same offer to the similar customers. This is typically done by performing the multi-variate numerical data the multi-variate numerical data clustering analysis.
The main goal of performing the actual clustering is to arrange a set of data items having an associated numeric n-dimensional vector of features into the number of homogeneous groups, called - “clusters”. In general, the entire clustering problem can be formulated as a certain objective similarity function minimization problem. As the similarity objective function, various of algebraic notions are used. The Euclidean distance between vectors in an n-dimensional Euclidean space is one of the most popular notions that is actively used in the vast of the existing clustering analysis techniques and algorithms. The figure below illustrates an example of performing data clustering:
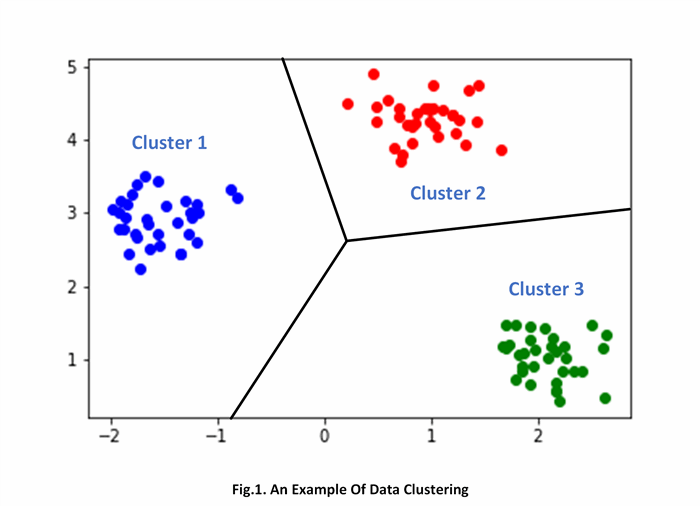
As you can see from the figure above, the various data are partitioned into the number of three clusters, each one is containing the most similar data.
Among the known clustering algorithms, that are based on minimizing a similarity objective function, k-means algorithm is most widely used. Given a set of t data points in real n-dimensional space, and an integer k, the problem is to determine a set of k points in the Euclidean space, called centers, as well as to minimize the mean squared distance from each data point to its nearest centroid. This measure is often called the squared-error distortion and this type of clustering belongs to the variance-based clustering category.
Clustering based on k-means is closely related to a number of other clustering and location problems. These include the Euclidean k-medians (or the multisource Weber problem) in which the objective is to minimize the sum of distances to the nearest center and the geometric k-center problem in which the objective is to minimize the maximum distance from every point to its closest center.
One of the most popular heuristics for solving the clustering problem based on using the k-means algorithm basically relies on a simple iterative method for finding a set of clusters. There is a number of variations of the k-means algorithm. Specifically, in this article, we will spotlight our discussion on the algorithm, proposed by Lloyd.
Moreover, we will discuss about the number of aspects of the classical k-means algorithm optimization aiming to improve the actual quality of clustering as well as to provide an efficient performance of the following algorithm.
Also, we will introduce various of metrics that allow us to evaluate the quality of clustering process such as the inertia or Dunn index.
Finally, we will discuss about an efficient implementation of the optimized k-means algorithm in C#.NET.
Background
In this chapter, we will introduce and formulate the k-means clustering algorithm, including the number of algorithm-level optimization that allow us to drastically improve the quality of clustering, as well as increase the performance of the clustering process itself.
Clustering Analysis (CA) Fundamentals
Clustering Analysis (CA) is the process of arranging a set of data items into a certain number of the groups, each one containing the items that are the most similar. These groups are called “clusters”. The “clustering” itself is commonly used for providing a better understanding of the data being analyzed, data compression or novelty detection.
The clustering analysis is an essential part of the data mining and statistics, that basically relies on the using of the number supervised machine learning algorithms that allow us to perform the actual clustering. These algorithms typically provide the various of approaches how specifically the entire clustering problem can be solved in general. There’re at least three popular clustering algorithms, such as either k-means or fuzzy c-means clustering, as well as the expectation-minimization (EM) algorithm addressing a partial or incomplete data clustering problem, etc.
Also, there’re the vast of ideas and points of view on how to determine the similarity of specific data and arrange these data into clusters. A popular approach for determining the similarity of data is to measure the actual Euclidean distance between specific data and group them into clusters based on the smallest distance criteria. The following approach is primarily used for determining the similarity of the data that can be easily represented as the number of vectors in n-dimensional Euclidean space. Each of these vectors consists of the number of numerical features $\bar{u}=\{u_1,u_2,u_3,…,u_{n-1},u_n\}$The actual distance between two vectors $\bar{u}$ and $\bar{v}$ can be measured by using the following Euclidean distance formula:
${\left\Vert{}{D}\right\Vert{}}^2=\sum_{i=1}^n{(u_i-v_i)}^2$
, where ${D}$ - the distance between two vectors of $\bar{u}$ and $\bar{v}$, $u_i$ and $v_i$ - the $i$-th component of vectors $\bar{u}$ and $\bar{v}$, $n$ - the number of features (i.e. dimensions of the Euclidean space);
The figure below illustrates the Euclidean distance between two data vectors computation:

According to this formula, two vectors are the most similar if and only if the actual difference between each of the components, and, thus, the overall value of the squared distance D , is the smallest.
To perform the multidimensional data clustering, we will use the fast and robust k-means algorithm in the favor of the other algorithms, it’s relatively efficient, providing the best clustering results for the distinct or well-separated synthetic data. The following algorithm is solely based on the distance measure by using the formula of Euclidean distance listed above.
K-means is the centroid-based clustering algorithm, capable of producing the clusters, each one is represented by a specific centroid. A “centroid” is a central data vector (i.e. point) that might or might not be included in the resultant set of data for each newly built cluster. According to the main idea of the clustering, if two data vectors are similar two its nearest centroid, based on the smallest distance criteria, then these two vectors are also similar (e.g. having the smallest distance of one to another). As a centroid for each newly built cluster we basically select a vector, representing a “center-of-the-mass” for a given set of data vectors, and, then, find all points having the smallest distance to its nearest centroid.
Before we ground our discussion on the k-means clustering algorithm, let’s discuss about some of the main considerations of producing clusters using the algorithm discussed:
- All the data points within a single cluster must be similar to one another;
- Particular data points from different clusters must be as different as possible;
According to the first consideration, the all data points assigned to a single cluster must be similar based on the intra-cluster distance criteria. The intra-cluster distance is a distance between data points within a single cluster, and the distance between to similar data points must not exceed the intra-cluster distance.
In turn, the inter-cluster distance, which is the distance between specific clusters (e.g. the clusters centers), must be much greater than the maxima intra-cluster distance to provide the high quality of clustering. The distance between the absolutely different data points must be greater than or equal to the inter-cluster distance. The difference between intra- and inter-cluster distances is shown in the figure below:

The following considerations are the fundamental principles of the optimal clustering process.
Importing And Preparing The Dataset
Here, we will delve into the discussion of the nature of the synthetic data we’re about to cluster using the k-means algorithm, as well as how to generate the synthetic input collection of data by using Python’s Sklearn library.
The first of all, let’s take a look at the synthetic data prior to performing the actual clustering. The term of “synthetic” basically refers to the data that meets the specific needs or certain conditions that cannot be revealed on the original real data. A dataset, in which all items are arranged into several groups is an example of those synthetic data, mentioned above.
As we’ve already discussed, the k-means algorithm can be used for clustering the multidimensional data, in which each item is represented by a vector in n-dimensional Euclidean space, which components is a set of numeric features. Also, each vector in the set is associated with a specific label of its group, class or category:

As can see from the figure above, each item in the dataset is a pair of 5-dimensional vector of features and its specific class label, to which the following item belongs. The numerical features of each vector basically represent specific parameter floating-point value. This could be, for example, a credit card balance, loan amount in finance, various characteristics of plants in biology, or whatsoever. A label of each particular item is a numerical or string value identifying a group items to which the following item is assigned. Further we will use the integer labels [0;N] for each group of items.
To generate the following dataset, we will implement a Python script listed below:
import numpy as np
import pandas as pd
from sklearn.datasets.samples_generator import make_blobs
X, labels = make_blobs(n_samples=1000, n_features=5, centers=6, cluster_std=0.60, random_state=0)
df = pd.DataFrame({'X': X[:,0], 'Y': X[:,1], 'Z': X[:,2], 'C': X[:,3], 'T': X[:,4], 'Label': labels}, columns=['X','Y','Z','C','T','Label'])
df.to_csv(r'd:\dataset.csv', index = None, header=None)
In this code, we will import the make_blobs function from sklearn.datasets.samples_generator module and use it to generate a set of data items along with their labels. The following functions accepts several of arguments such as the number of items to generate n_samples = 600, the number of features of each item’s vector n_features=5, the number of cluster centers = 6, standard deviation of the clusters cluster_std = 0.60, and random numbers generator state random_state=0. The following function returns a tuple of arrays of either vectors or its labels being generated.
After we’ve generated the dataset, let’s now export the following dataset to .csv file format. To do that we will use the Python’s Pandas data frame. The Pandas data frame normally instantiated with generic template, passing two arguments to the data frame constructor df = pd.DataFrame(…). The first argument is a list containing data for each column of the dataset previously generated: {'X': X[:,0], 'Y': X[:,1], 'Z': X[:,2], 'C': X[:,3], 'T': X[:,4], 'Label': labels} and the second one is the list of column label names: columns=['X','Y','Z','C','T','Label']. After we’ve created the data frame, we now can export the data to .csv-file. This typically done by invoking df.to_csv(r'dataset.csv', index = None, header=None) method.
Finally, the following dataset can be used by the code in C#.NET to perform the actual clustering.
K-Means Clustering Algorithm
Initialization
The initialization phase of the k-means algorithm is rather intuitively simple. During the initialization phase, we normally select k – random points in the Euclidean space as a set of initial centroids prior to performing the actual clustering.
However, the following method has the number of disadvantages, which leads to the sub-optimal clustering problem occurrence. Specifically, the distance between randomly selected centroids, in the most cases, is not optimal (e.g. the distance between particular centroids is very small). The following normally has two main outcomes in either a poor quality of clustering or sufficient performance degrades.
Obviously, that, to perform an optimal clustering, we need a slightly different approach for finding an optimal set of initial centroids, discussed below.
K-Means++ Initialization
As a workaround to the sub-optimal clustering problem, we will formulate the k-means++ initialization algorithm that allows us to drastically improve the quality of clustering provided by the classical k-means procedure, as well as to increase its performance and lower the computational complexity. Normally we use the k-means++ alternative to achieve two main goals:
- Improve the convergence and quality of clustering provided by the classical k-means algorithm, over its known shortcomings and limitations;
- Provide a better performance of the NP-hard k-means clustering procedure, optimizing the iterations, and, thus, reducing its computational complexity to only $p = O(log(k))$, where $k$ - the number of initial centroids, without re-engineering the entire algorithm itself;
The entire initialization procedure basically relies on performing the several steps such as either Euclidean, Lloyd’s or native k-means++. Euclidean step is a preliminary step, during which we are performing a search to find a pair of the first and second initial centroids, based on the maxima Euclidean distance magnitude. In turn, the Lloyd’s step is very common to both k-means++ and k-means clustering procedures itself. During this step we actually pre-build a set of initial clusters, mapping each point onto a specific existing centroid, and, thus, building an initial cluster. This is typically done to find a point and centroid with an optimal distance. The k-means++ is the final step during which we survey the distances between a point and each already existing centroid, selecting new optimal centroids, based on the largest distance measure.
According to the k-means++ procedure, we no longer have a need to randomly seed arbitrary points $\forall p\in \mathbb{R}^{n}$ in the Euclidean space and use them as the set of initial centroids prior to performing the actual clustering. Although, the number of initial centroids $k$ still must be specified.
During the k-means++ initialization phase, we will be randomly selecting only the first centroid, among those already existing data points $\forall {t_k}\in {T}$, and then use a slightly different algorithm to select the other centroids optimally. Let’s recall that, in this case, each centroid being selected using k-means++ procedure is a point in the set of already existing data points $T$, rather than an arbitrary point in the n-dimensional Euclidean space.
The main idea of the k-means++ algorithm is that the entire process of centroids computation basically relies on the measure of optimal distance between those centroids being selected. It’s highly recommended that the actual distance between centroids must be as largest as possible.
While performing the initialization, we all the way keep on finding centroids with an optimal distance. After we’ve randomly selected the first centroid ${c_1}$ we can compute a point as the second centroid ${c_2}$ with the largest distance to centroid ${c_1}$, and, that is the first-largest distance. Then, we compute a specific point and its nearest centroid ${c_1}$ or ${c_2}$ so that the distance between the point and one of the centroids is the second-largest distance. The following point is taken as the third centroid ${c_3}$. To find the fourth centroid ${c_4}$ we do exactly the same, computing a point with the third-largest distance to one of the centroids ${c_1}$, ${c_2}$ or ${c_3}$, and so on.
The k-means++ algorithm can be formulated as follows:
- Given a set of data points $T=\{t_1,t_2,t_3,...,t_{n-1},t_n\}$ and the number of initial clusters $k$;
- Randomly select a point $\forall{t}$ as the first centroid $c_1 = RND\{\overline{T}\}$; from an input set of points. In this case, we can take any existing point $\forall{t}$ in the set without any limitations;
- Compute the distance $d(t_k)$ of each point in the set to the first centroid $c_1$ and select a point $t_j$ with the largest distance as the next centroid $c_2 = \forall{t_j}|max_j\{d(t_j)\}$;
- Compute the distance $d(t_k)$ of each point to its nearest centroid in a set of centroids that have already been selected (e.g. $C = \{c_1,c_2,c_3,...,_c{n-1},c_n\}$);
- Select a point $t_s$ having the largest distance as the next centroid $c_m = \forall{t_s}|max_s\{d(t_s)\}$, and add it to the set of centroids ($C\leftarrow c_m$);
- Proceed with steps 3 and 4 until the required number of $k$ centroids have been selected;
According to the k-means++ procedure, we must make sure that at least two centroids have already been selected before computing the other centroids. During this phase, the resultant set of centroids must be initialized with a single value of randomly selected point as the first centroid $c_1$. The second centroid $c_2$ is selected by computing the distance $d(t_k)$ of each point to the first centroid $c_1$ and choosing a point $\forall{t_j}$ with the largest distance to the following centroid. This is typically done to improve the inter-cluster distance prior to performing the actual clustering. After, the second centroid $c_2$ has been successfully selected, we add the following point $c_m = t_j$ to the set of centroids $C \leftarrow c_m$. The following trivial operation basically refers to the Euclidean step of the algorithm, being discussed. The Fig. 5 illustrates the process of selecting the first and second initial centroids $c_1$ and $c_2$, respectively:

Since both centroids $c_1$ and $c_2$ have already been selected, now, we can compute the rest of other centroids (e.g. $c_3,c_4,c_5,...$ ). To do that, for each point, we must iteratively compute the distance $d(t_k)$ to all existing centroids in the set $C$ and associate the current point $t_k$ with centroid $c_n$ for which the following distance is the smallest until each of the points would belong to a particular centroid. This step is very common for both k-means++ and classical k-means algorithms and called the “Lloyd’s step”. Then, according to the native k-means++ algorithm, a point $t_s$ with the largest distance to its nearest centroid $c_n$ is selected as the next centroid $c_m\leftarrow t_s$, and added to the set of centroids $C$. Normally, we repeat the following computations until the required number of centroids has been found. The entire process of finding the rest of other centroids in the set is shown in Fig.6. below:

As you’ve might already noticed, we normally proceed with k-means++ initialization process until we’ve finally ended up with a set of centroids being selected as well as the number of initial clusters built during the algorithm Lloyd’s step. Further, this number of initial clusters is added to the output set of already existing clusters and the new clusters are produced by re-computing a center of the mass magnitude (i.e. “centroids”) for each particular existing cluster, being processed. This, in turn, allows to improve the performance of the k-means clustering at the algorithm level. The following topic is thoroughly discussed in one of the succeeding chapters of this article.
In the previous paragraphs, we’ve already discussed that the k-means++ initialization process is mainly based on finding the centroids with the largest optimal distance. However, as it might have seemed to us, the algorithm for finding an optimal set of initial centroids could be different. Specifically, we can compute the distance between pairs of points and then select those points with the largest distance. Obviously, that, the following algorithm fails since the distance between to two or more arbitrary points taken as the centroids might not be an optimal. For example, we’ve found a set of three centroids $c_1$, $c_2$ and $c_3$. The distances between pairs of centroids $c_1$ and $c_2$, as well as $c_2$ and $c_3$ are optimal, but the distance between $c_1$ and $c_3$ is not. The following cause is the proof that we still need to conform to the k-means++ initialization procedure, instead.
In fact, the k-means++ initialization procedure is the only possible algorithm addressing an optimal initial centroids selection. The following procedure is solely based on a technique of selecting centroids having an optimized distance between them, and, thus, ensuring that k-means algorithm itself will successfully converge at the very first steps of the clustering process, significantly reducing the number of operations performed. Also, there’s the number of k-means++ algorithm variations such as either distance- or probability-based. However, probability distribution-based k-means++ procedure, similar to the generic k-means initialization, sometimes tends to provide poor results of the initial centroids selection, due to the several randomization issues.
Finally, in the chart below we will compare the results of the initial centroids selection by using the either k-means++ procedure or the generic k-means random initialization:

Performing K-Means Clustering
After we’ve thoroughly discussed about the initialization phase, let’s now spend a moment and take a short glance at the k-means clustering procedure. According to the main idea of the k-means algorithm we need to arrange points with the smallest distance into multiple of groups called “clusters”, and, since the newly built clusters have been produced, re-compute a centroid for each of these clusters, based on the process of finding the “center of the mass” magnitude, using the method discussed in the next paragraphs.
After brief introduction, let’s formulate the classical k-means algorithm, which is very simple:
- Given a set of $k$ – centroids $C=\{c_1,c_2,c_3,...,c_{k-1},c_k\}$ and a set of data points $T=\{t_1,t_2,t_3,...,t_{n-1},t_n\}$;
- For each centroid $\forall{c_i}$, find a subset of points $\hat{T}$ having the nearest distance to the current centroid $c_i$ and associate these points with the following centroid, creating a newly built cluster;
- Re-compute the centroids of each of the newly built clusters based on the “center-of-the-mass” magnitude, appending each new centroid being computed to the set of centroids $C$;
- Perform a check if the centroid of each already existing cluster has not changed and the points selected are not within the same clusters (e.g. we’re not producing the similar clusters, containing duplicate points, which have already occurred in the previously built clusters);
- If not, proceed with steps 1,2 and 3, otherwise terminate the k-means clustering process;
Since, we’re already given a set of the initial centroids $C$ for each specific centroid $c_i$ we can compute a cluster containing the data points in $T$, for which the distance to the current centroid $c_i$ is the smallest. To do that, for each particular point $t_k \in T$, we must compute a distance to each of the centroids $c_i \in C$, determining the centroid $c_j$ with the smallest distance to the current point $t_k$, and assigning a subset of points $\hat{T}$ to a newly built cluster with centroid $c_j$. The following operation basically refers to the Lloyd’s step of the algorithm, previously discussed.
After we’ve computed the new clusters, it’s time to re-compute the centroids to have an ability to produce the new clusters during the next phase of the clustering process. This is typically done by using the “center-of-the-mass” equation, that yields the following computation. To find a center of the mass, for all points in $\hat{T}$ we must compute an average/mean of each coordinate in the n-dimensional Euclidean space $t_k\in\mathbb{R}^n$. Here’s an equation that illustrates such computation:
$v_i=\frac{1}{c_i}*\sum_{j=1}^{c_i}x_j$
where $v_i$ is the new centroid of the $i$ – th cluster, $c_i$ - the number of points in the $i$ – th cluster, $x_j$ - a point belonging to the $i$ – th cluster $\forall x_j \in \hat{T}$;
As the result of performing those computations, we’ve obtained a point, representing a new cluster’s centroid. We normally proceed with the following computations until we’ve found a new centroid for each of the already existing clusters:

Further, we will use these centroids to find the new clusters, proceeding with the same Lloyd’s step of the k-means algorithm, discussed in one of the previous paragraphs.
Finally, here’s one more aspect of the clustering process that we will discuss is the k-means algorithm stopping criteria. There are at least three criterions that can be used to determine when exactly the k-means clustering process must be terminated:
- The new centroids that have been re-computed don’t change and are equal to the centroids of already existing clusters;
- The new clusters consist of the same data points that have already occurred in the previously built clusters;
- The limit of iterations has been reached;
Under one of these conditions we can terminate the k-means clustering process, considering that the following process has successfully converged, and we’ve ended up with a required number of $k$- clusters, each one is containing the most similar data points.
Evaluating K-Means Clustering Algorithm
There’s the number of evaluation metrics, such as either the inertia magnitude or Dunn index, that allow us to measure a quality of clustering. By evaluating the inertia, we actually compute the sum of distances of all points to the centroid of each cluster, and, then add up each of these sums together. Actually, by computing the inertia we evaluate the sum of intra-cluster distances. Finally, we consider that as the lesser the inertia value as the quality of clustering is higher. The following formula illustrates the inertia metric computation:
$I=\sum_{i=1}^{k} \sum_{j=1}^{c_i}|x_j-c_i|^2$
, where $I$ – the inertia value, $k$ – the number of clusters, $c_i$ – the centroid of $i$ – th cluster, $x_j$ - the $j$ – th point within the $i$ – th cluster.
Also, the inertia value can be used to determine the initial number of clusters for performing the most optimal clustering. In this case we sequentially increase the number of initial clusters $k$ and then compute the inertia, until the inertia value has not varied and becomes constant. After that, take the initial number of clusters $k$ for which the inertia value has not been changed.
Dunn index is another metric by using which we can effectively evaluate the quality of clustering. The following metric basically represents a ratio between the minimum of inter-cluster distances and the maximum of intra-cluster distances. Unlike the inertia value, the Dunn index magnitude largely depends on the distance between clusters. In the most cases, to provide a high-quality clustering we want to maximize the Dunn index value. The formula below illustrates the Dunn index computation:
$Dunn_{index}=\frac{min\{inter-cluster \space distances\}}{max\{intra-cluster \space distances\}}$
As you can see from the formula above, the maximum value of Dunn index can be obtained if and only if the minima inter-cluster distance is the highest. Also, we get the same maximum of Dunn index when the maxima intra-cluster distance is the smallest. And, the following is the ideal case of the clustering itself, since we build a set of the most appropriate clusters, each one is containing the items which are the most similar, whilst the difference between specific items from the distant clusters itself is very high.
Using the code
Here, we will discuss how to implement the number of functions, performing the k-means clustering. The very first function I've implemented is the function LoadDataFromFile(...) that loads the multi-dimensional clustering dataset from .csv file:
static List<tuple<list<double>, string>> LoadDataFromFile(string filename)
{
List<tuple<list<double>, string>> Items =
new List<tuple<list<double>, string>>();
using (System.IO.StreamReader file =
new System.IO.StreamReader(filename))
{
string buf = "\0";
while ((buf = file.ReadLine()) != null)
{
List<double> features = new List<double>();
foreach (string param in buf.Split(',').ToArray())
if (Regex.Match(param, @"[.]", RegexOptions.IgnoreCase).Success)
features.Add(Double.Parse(param, CultureInfo.InvariantCulture));
Items.Add(new Tuple<list<double>, string>(features,
buf.Split(',').ElementAt(buf.Split(',').Length - 1)));
}
file.Close();
}
return Items;
}
</list<double></double></double></tuple<list<double></tuple<list<double></tuple<list<double>
The following code listed above, opens a .csv-file and reads each line from the file, iteratively splitting it into a list of values. For each value it performs a check if its a floating-point value. If so, it appends the following value to the list of features, building a multi-dimensional vector, which is then added to the list of items along with its label (e.g. the last comma-separated value in the current line). At the end of execution the following function returns a list of item tuples consisting of a vector of features and its label.
EuclDist(...) - another function that I've implemented beforehand. The following function performs the multi-variate Euclidean distance value computation and accepts two main arguments such as either the first and second vectors of features, respectively, to compute the distance (i.e. "similarity") between these two vectors:
static double EuclDist(List<double><double> params1,
List<double><double> params2, bool squared = false)
{
double distance = .0f;
for (int Index = 0; Index < params1.Count(); Index++)
distance += Math.Pow((params1[Index] - params2[Index]), 2);
return !squared ? Math.Sqrt(distance) : distance;
}
</double></double>
There're two specializations of this function for either a regular or squared Euclidean distance computation. As the result of the following function execution, we get a floating-point value of the Euclidean distance between two n-dimensional vectors of features. The following function is primarily used by Euclidean_Step(...) and Lloyd_Step(...) functions to compute the specific distance values:
static int Euclidean_Step(List<tuple<list<double>,
string>> items, int centroid)
{
List<tuple<int, double="">> dists = new List<tuple<int, double="">>();
for (int Index = 0; Index < items.Count(); Index++)
dists.Add(new Tuple<int, double="">(Index,
EuclDist(items[centroid].Item1, items[Index].Item1, true)));
return dists.Find(obj => obj.Item2 ==
dists.Max(dist => dist.Item2)).Item1;
}
</int,></tuple<int,></tuple<int,></tuple<list<double>
The following function listed above, accepts two main arguments of the list of items as well as the index of the item selected as the first centroid.
Lloyd_Step(...) is the main function by invoking which we basically perform the actual clustering. The following function is used by both k-means++ and k-means routines to partition the dataset by the nearest distance to each of the centroids in the list of centroids. Here's an implementation of Lloyd_Step(...) function:
static List<Tuple<int, List<int>>> Lloyd_Step(
List<Tuple<List<double>, string>> items,
List<int> centroids, List<List<double>> c_mass = null)<tuple<int, list=""><tuple<list<double><int><list<double>
{
List<tuple<int, list="">>> clusters =
new List<tuple<int, list="">>>();
if (centroids != null)
{
for (int Index = 0; Index < centroids.Count(); Index++)
clusters.Add(new Tuple<int, list="">>(
centroids[Index], new List<int>()));
}
else
{
for (int Index = 0; Index < c_mass.Count(); Index++)
clusters.Add(new Tuple<int, list="">>(Index, new List<int>()));
}
for (int Index = 0; Index < items.Count(); Index++)
{
double dist_min = .0f; int cluster = -1;
if (centroids != null)
{
for (int cnt = 0; cnt < centroids.Count(); cnt++)
{
double distance = EuclDist(items[Index].Item1,
items[centroids[cnt]].Item1, true);
if ((distance <= dist_min) || (cluster == -1))
{
dist_min = distance; cluster = cnt;
}
}
var cluster_target = clusters.Find(
obj => obj.Item1 == centroids[cluster]);
if (cluster_target != null)
cluster_target.Item2.Add(Index);
}
else
{
for (int cnt = 0; cnt < c_mass.Count(); cnt++)
{
double distance = EuclDist(items[Index].Item1, c_mass[cnt], true);
if ((distance <= dist_min) || (cluster == -1))
{
dist_min = distance; cluster = cnt;
}
}
var cluster_target = clusters.Find(
obj => obj.Item1 == cluster);
if (cluster_target != null)
cluster_target.Item2.Add(Index);
}
}
return clusters;
}
</int></int,></int></int,></tuple<int,></tuple<int,></list<double></int></tuple<list<double></tuple<int,>
The following function listed above, accepts three arguments of either an input list of items, list of centroids indices or a list of points representing the new clusters centers. For each item it computes the Euclidean distance to each centroid or point in the list, performing a search to find a centroid for which this distance is the smallest. Then it assigns the following item to a cluster with a centroid having the smallest distance. The following function actually performs the entire dataset partitioning. Finally, the following function returns a list of tuples, each one is consisting of a centroid index and a list of item indices.
To perform k-means++ initialization, we will implement the following function that basically relies on using the Euclidean_Step(...) and Lloyd_Step(...) functions:
static Tuple<List<int>, List<Tuple<int, List<int>>>> KmeansPlusPlus(
List<Tuple<List<double>, string>> items, int k)
{
List<int> centroids = new List<int>() {
new Random().Next(items.Count())
};
if (centroids.Count() == 1)
centroids.Add(Euclidean_Step(items, centroids[0]));
List<Tuple<int, List<int>>> targets = null;
for (int count = k - 2; count >= 0; count--)
{
List<Tuple<int, List<int>>> clusters =
Lloyd_Step(items, centroids);
double dist_max = .0f; int cmax_index = -1, dmax_index = -1;
for (int Index = 0; Index < clusters.Count(); Index++)
{
int centroid = clusters[Index].Item1;
for (int pt = 0; pt < clusters[Index].Item2.Count(); pt++)
{
double distance = EuclDist(items[centroid].Item1,
items[clusters[Index].Item2[pt]].Item1);
if ((distance > dist_max) ||
(cmax_index == -1) || (dmax_index == -1))
{
dist_max = distance;
cmax_index = Index; dmax_index = pt;
}
}
}
if (count > 0)
centroids.Add(clusters[cmax_index].Item2[dmax_index]);
targets = (clusters.Count() > 0) && (count == 0) ? clusters : null;
}
return new Tuple<List<int>, List<Tuple<int, List<int>>>>(centroids, targets);
}
To perform the actual k-means clustering we will implement the following function:
static List<Tuple<int, List<int>>> KMeans(
List<Tuple<List<double>, string>> Items, int k)
{
Tuple<List<int>, List<Tuple<int,
List<int>>>> result = KmeansPlusPlus(Items, k);
List<Tuple<int, List<int>>> clusters_target =
new List<Tuple<int, List<int>>>();
List<int> centroids = result.Item1;
List<Tuple<int, List<int>>> clusters = result.Item2;
while (clusters.Count() > 1)
{
List<List<double>> centroids_new =
RecomputeCentroids(clusters, Items);
List<Tuple<int, List<int>>> clusters_new =
Lloyd_Step(Items, null, centroids_new);
for (int clu = 0; clu < clusters.Count(); clu++)
{
if ((Compare(clusters[clu].Item2, clusters_new[clu].Item2)))
{
clusters_target.Add(clusters[clu]);
clusters.RemoveAt(clu); clusters_new.RemoveAt(clu); clu--;
}
}
if (clusters_new.Count() > 1)
clusters = clusters_new;
}
return clusters_target;
}
The function listed above performs the actual k-means clustering. First, it invokes KmeansPlusPlus(...) function to get a list of initial centroids and pre-built clusters. After that, it performs a simple iteration during which the centroids of already existing clusters are re-computed. Further, those new centroids are used by Lloyd_Step(...) function to partition the entire dataset into a set of new clusters. Then it's performing a check if the k-means procedure has converged and we're not producing the same clusters. If not, it proceeds with the next iteration of the k-means clustering process. Otherwise, the following function returns a list of newly built clusters. To re-compute the new centroids I've implemented the following function:
static List<List<double>> RecomputeCentroids(
List<Tuple<int, List<int>>> clusters,
List<Tuple<List<double>, string>> Items)
{
List<List<double>> centroids_new =
new List<List<double>>();
for (int clu = 0; clu < clusters.Count(); clu++)
{
List<int> c_items = clusters[clu].Item2;
List<double> centroid = new List<double>();
for (int i = 0; i < Items[c_items[0]].Item1.Count(); i++)
{
if (Items[c_items[0]].Item1.Count() > 0)
{
double avg = .0f;
for (int Index = 0; Index < c_items.Count(); Index++)
avg += Items[c_items[Index]].Item1[i] / c_items.Count();
centroid.Add(avg);
}
}
centroids_new.Add(centroid);
}
return centroids_new;
}
To get the new centroids, we normally compute an average (i.e. "center-of-the-mass") of each coordinate for each item within a single cluster to obtain a point which is a centroid for a specific cluster.
Also, there's another function that performs a check if the old and new clusters are not intersecting. Specifically, if the newly built clusters are not included in the old ones:
static bool Compare(List<int> list1, List<int> list2)
{
return list2.Intersect(list1).Count() == list2.Count();
}
Finally, let's discuss about the main code that performs the actual k-means clustering by using the functions we've introduced above:
static void Main(string[] args)
{
Console.WriteLine("K-Means Clustering Algorithm v.1.0 by Arthur V. Ratz @ CodeProject.Com");
Console.WriteLine("======================================================================");
string filename = "\0";
Console.Write("Enter a filename: ");
filename = Console.ReadLine();
int k = 0;
Console.Write("Enter a number of clusters: ");
k = Int32.Parse(Console.ReadLine()); Console.WriteLine();
List<Tuple<List<double>, string>> Items =
LoadDataFromFile(filename);
List<Tuple<int, List<int>>> clusters_target =
KMeans(Items, k);
for (int clu = 0; clu < clusters_target.Count(); clu++)
{
Console.WriteLine("Cluster = {0}", clu + 1);
for (int Index = 0; Index < clusters_target[clu].Item2.Count(); Index++)
{
for (int Item = 0; Item < Items[clusters_target[clu].Item2[Index]].Item1.Count(); Item++)
Console.Write("{0} ", Items[clusters_target[clu].Item2[Index]].Item1[Item]);
Console.WriteLine("{0}", Items[clusters_target[clu].Item2[Index]].Item2);
}
Console.WriteLine("\n");
}
Console.ReadKey();
}
The following code loads the dataset from .csv-file by invoking the LoadDataFromFile(...) function and then executes the KMeans(...) function to perform the actual clustering. Finally, it outputs the results of clustering:

Points of Interest
As we’ve already discussed, the entire k-means clustering process can be drastically optimized by using the k-means++ initialization procedure. In this case, the using of k-means++ initialization benefits in both the quality and performance of the clustering process, providing an ability to reduce the overall computational complexity of the classical NP-hard k-means algorithm to just $p = O(log(k))$, where $k$ is the number of clusters in the resultant set. Besides of the set of optimal initial centroids, k-means++ initialization can be used for producing a set of initial clusters, the k-means clustering process starts with. Also, the using of k-means++ initialization ensures that the k-means clustering process will be completed and successfully converge with the minima number of iterations, providing the most appropriate results of the actual clustering. Specifically, each cluster will contain the most similar data points, especially while performing the exclusive clustering operations, during which, each of the points is assigned to a particular cluster and cannot be included in more than one cluster simultaneously.
Moreover, the performance of sequential code fragments, performing the actual k-means clustering can be easily transformed into parallel using the various of existing high-performance computing (HPC) libraries and frameworks, providing even more performance of the clustering process itself.
History
- Jan 11, 2020 - The first version of this article has been published
