FA: A Unicode Automata and Regular Expression Engine

• Download source - 1.1 MB

Introduction

This codebase is my new Unicode capable finite automata and regular expression engine. It fills a gap in Microsoft's Regular Expression offering, which only deals with matching rather than lexing (I'll explain the difference), relies on a less efficient but more expressive regular expression engine, and can't stream.

This engine is designed primarily for lexing rather than matching, and it's designed to be efficient and to be streaming. In other words, it fills the holes in what Microsoft offers us in .NET.

Prerequisites

This article assumes a familiarity with finite automata and regular expressions. If you need some background, try my article on how to build a regex engine.

It is strongly recommended that you install GraphViz and place it in your PATH. This will allow you to call RenderToStream() and RenderToFile() to get images of the state machine graphs which are a godsend for debugging.

I use deslang and csbrick as pre-build steps to build Rolex, the included lexer generator. Because of this, I've included the binaries in the solution folder. They are not harmful, and they are necessary for the project to build. The source code for each is available at the links above. You can always delete them, but you'll have to delete the pre-build steps from Rolex to get the mess to build again.

Conceptualizing this Mess

Finite automata is virtually always used at some phase during regular expression matching and/or compilation regardless of implementation. This is in part due to the dual nature of regular expressions and finite automata. One can exactly describe the other and vice versa. This makes finite automata useful for graphing and otherwise analyzing or interpreting a regular expression, from its grotty internals on outward, and in turn makes regular expressions useful for describing finite automata. They're a natural pair, like peanut butter and jelly. Consequently, this library includes both.

One of the major difficulties in supporting Unicode is it's no longer practical for an input transition to be based on a single character value. This is because Unicode ranges are sometimes huge - 21-bits, or a cardinality of 0x110000 - and we must avoid expanding them to their individual characters at all costs or it will take a very long time to process. Especially challenging was the DFA subset/powerset construction which had to work with those ranges as well. In the end, I borrowed a technique from the Fare library, which saved me $50 and change on a book I would have needed. Happy find.

This library is a streamlined and rewritten version of my previous offerings, designed specifically for Unicode inputs. Consequently all input values internally are kept as UTF-32, stored as ints.

The FA class is the key to the library and handles all of the operations from parsing regular expressions to lexing. Each FA represents a single state in a finite state machine. They are connected via InputTransitions and EpsilonTransitions. Two things to always be aware of are the root state of the machine, and the extents of the machine as gathered by taking the closure. The closure of a state is simply the set of all states reachable from that state either directly or indirectly, including itself. The closure of x therefore, represents the entire machine for FA x. The astute reader may notice this means machines can be nested inside machines, and this is true. There is no concept of an overarching machine, just the root state of the machine by which it can determine the rest of the states. The root state is always "q0" if graphed. There are no parents, so we can only move along the graph in a single direction. The graphs can contain loops and thus be infinitely recursive. Because of this, when traversing the graph, one must be careful to not retraverse nodes already seen. This is handled by the FillClosure() and FillEpsilonClosure() methods. There shouldn't be a case where you actually have to concern yourself with that.

The library deals with lexing, not matching - at least not directly. Lexing is the process of breaking input up into lexemes or tokens with an associated symbol for each. This is usually passed along to a parser. A normal regular expression match can't do this. Lexing is basically matching a composite regular expression where each subexpression has a special tag - a "symbol" attached to it. There is no way to attach symbols to a regular match expression, and that doesn't make sense to do so.

You'll usually want to build a lexer, so basically, the steps to produce a lexer are this:

1. Build an array of FAs, usually parsed from regular expressions using Parse(). Make sure to set the accept symbols to a unique value for each expression you want to distinguish between.
2. Call ToLexer() with the array to get an FSM back you can use to lex.
   Now you have a working NFA lexer, but you'll probably want to convert it into something more efficient:
3. Build an array of ints to represent your symbol table. Each entry is the id of the FA in that ordinal position. This is optional but recommended otherwise you won't know what your ids are because they will be automatically generated in state order.
4. Call ToDfaStateTable() with the symbol table you created to get an efficient DFA table you can use to lex. Once you have that, you can call the Lex() method to lex your input, or alternately create a Tokenizer in order to lex with an FA. For a more efficient tokenizer, use the Rolex tool to generate one.

Once you have that, you can lex either by calling one of the Lex() methods, or create a Tokenizer to do your lexing. The Tokenizer, like the non-static Lex() method, will accept an FA that can either be a DFA or an NFA but the static Lex() method that takes a DFA state table is the most efficient.

We're starting to get into the code so let's move on to the next section.

Coding this Mess

First note that I expanded the transitions to accept ranges:

partial class FA 
{
    public readonly Dictionary<KeyValuePair<int,int>,FA> InputTransitions = 
                                          new Dictionary<KeyValuePair<int,int>,FA>();
    public readonly HashSet<FA> EpsilonTransitions = new HashSet<FA>();
    public int AcceptSymbol = -1;
    public bool IsAccepting = false;
...

As you can see, we're just using simple fields on this. The KeyValuePair<int,int> is a range consisting of two UTF-32 Unicode values indicating the first and final character in the range. Each one maps to its next state as normal. The rest of the FA remains unchanged from a non-Unicode version.

Other than that, as mentioned, the FA class contains methods for dealing with every aspect of an FSM, including parsing from a regular expression. One again, each FA represents a single state in the automaton. FA instances are unaware of their root, so every operation acts as though the FA instance you're acting on is the root of the FSM, or state q0. An FSM consists of the root state and all states reachable from that state - the closure. If you take the closure of the FSM using fa.FillClosure(), the first state in the returned collection will always be fa.

There are several static methods for composing thompson constructions like Literal(), Set(), Optional(), Or() and Repeat() as well as a Parse() method for parsing from a regular expression.

Basically, you can use a combination of these to compose your expression or your lexer. Once you have built your FSM using these methods, you can use it to lex or match. It is recommended you use Microsoft's regular expression engine to do the latter, unless you need to stream the input.

FA is not designed with matching in mind, but you can improvise a matcher using the built in tokenizer, and report anything where the SymbolId is not negative.

Keep in mind that all input values that FA accepts are expected to be UTF-32 and that means they must be translated from a UTF-16 character value to a UTF-32 integer value. You can do that on strings and char arrays with UnicodeUtility.ToUtf32. Otherwise for characters, you can use char.ConvertToUtf32().

As for the rest, let's let the demo code do the talking:

var kws = "abstract|as|ascending|async|await|base|bool|break|byte|case|catch|char|checked|
           class|const|continue|decimal|default|delegate|descending|do|double|dynamic|else|
           enum|equals|explicit|extern|event|false|finally|fixed| float |for|foreach| get | 
           global |goto|if|implicit|int|interface|internal|is|lock|long|namespace|new|null|
           object|operator|out|override|params|partial|private|protected|public|readonly|
           ref|return|sbyte|sealed|set|short|sizeof|stackalloc|static|string|struct|switch|
           this|throw|true|try|typeof|uint|ulong|unchecked|unsafe|ushort|using|var|virtual|
           void|volatile|while|yield";
// shorten this so our state graphs aren't so big:
kws = "as|base|case";
var lexa = new FA[]
{
    FA.Parse(kws,0), // keyword
    FA.Parse("[A-Z_a-z][0-9A-Z_a-z]*", 1), // id
    FA.Parse(@"""([^""]|\\[^n])*""", 2),   // string
    FA.Parse("[\r\n\t\v\f ]+", 3)          // whitespace
};

// build our lexer
var nfa = FA.ToLexer(lexa);
nfa.TrimNeutrals();
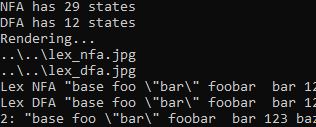
Console.WriteLine("NFA has " + nfa.FillClosure().Count + " states");

// minimize
var dfa = nfa.ToDfa();
dfa.TrimDuplicates();
Console.WriteLine("DFA has " + dfa.FillClosure().Count + " states");

var baseFn = @"..\..\lex_";
var fn = baseFn + "nfa.jpg";
Console.WriteLine("Rendering...");
Console.WriteLine(fn);

// graphviz might not be installed:
try
{
    nfa.RenderToFile(fn);
}
catch
{
    Console.WriteLine("Rendering aborted - GraphViz is not installed. 
                       Visit GraphViz.org to download.");
}
            
fn = baseFn + "dfa.jpg";
Console.WriteLine(fn);
try
{
    dfa.RenderToFile(fn);
}
catch { }
var text = "\"\\\"foo\\tbar\\\"\"";
text = "\"base foo \\\"bar\\\" foobar  bar 123 baz -345 fubar 1foo *#( 0\"";
Console.Write("Lex NFA " + text + ": ");
var sb = new StringBuilder();
// lex NFA
Console.WriteLine(nfa.Lex(UnicodeUtility.ToUtf32(text).GetEnumerator(), sb));
                       
// build a simple symbol table so our ids match our NFA
var symids = new int[lexa.Length];
for (var i = 0; i < symids.Length; i++)
    symids[i] = i;

// create DFA state table
var dfaTable = dfa.ToDfaStateTable(symids);

// Use built in lexing method
Console.Write("Lex DFA " + text + ": ");
Console.WriteLine(FA.Lex(dfaTable,UnicodeUtility.ToUtf32(text).GetEnumerator(), sb));

// use tokenizer
var tokenizer = new Tokenizer(dfa, text);
foreach (var token in tokenizer)
    Console.WriteLine("{0}: {1}", token.SymbolId, token.Value);

This is just one way to use this library. Another way is to use it to do code generation to generate lexers.

And that's it!

Limitations

The FA engine matches fairly quickly, but the minimization could be quite a bit faster. There is also currently no anchor support.

History

• 1^st February, 2020 - Initial submission
• 4^th February, 2020 - Fixed bug in FA.Parse()