A data structure that looks like an ordered array and behaves like a hash table. Any value can be accessed by its index or by its name. It preserves the elements' order and uses two memory blocks. Therefore, it has an initial size, and collisions do not cause new allocations. When resized, it drops deleted items and resets its hash base.
Introduction
Hash tables are data structures that enable locating values using string keys. Some hash tables are fast in insertion, and some in finding values. A few implementations suffer from slow deletion, memory fragmentation, or their performance degrade with more items. Most hash tables do not store items by order, or retrieve a value using an index, and have to consume more memory for fast searching or to keep track of the order if they support that. However, this implementation may offer more speed with less trading.
Implementation
For a data structure to retrieve values using numbers, it needs to be a linear array, and when its memory block reaches its limit, it expands to a new heap and moves all of its items from the old memory to the new one. Therefore, it has to be a one-dimensional array. Though it is not just an array or a hash table, it is both.
template <typename Value_>
class HArray {
size_t size_{0};
size_t capacity_{0};
Value_ *storage_{nullptr};
};
The variable size_ holds the number of items, capacity_ is for the size of the heap/memory block, and storage_ points to the location of the first value. Still, items have to store more than just values; they need the variable Key and its hash for HArray to function as a hash table.
template <typename Key_, typename Value_>
struct HAItem {
size_t Hash;
Key_ Key;
Value_ Value;
};
template <typename Key_, typename Value_>
class HArray {
size_t size_{0};
size_t capacity_{0};
HAItem<Key_, Value_> *storage_{nullptr};
};
A linear array insertion looks like the following:
private:
void insert_(Key_ key, Value_ value, size_t hash) {
if (size_ == capacity_) {
}
HAItem<Key_, Value_> &item = storage_[size_];
item.Hash = hash;
item.Key = key;
item.Value = value;
++size_;
}
But, for the hash table to work, it needs a searching technique and deals with collisions. One way to solve that is to add a linked list by adding an extra variable Next to the structure, to point to the item that comes next. Therefore, the new structure looks like:
template <typename Key_, typename Value_>
struct HAItem {
size_t Hash;
HAItem *Next;
Key_ Key;
Value_ Value;
};
The searching technique compares a given key to a stored one. It locates it by dividing its hash value over (capacity – 1) and the remainder – of that division point to an index, a location in the allocated heap. If the compare function sought that the two keys are different, then it checks the pointer Next to see if its item holds the same key or not, and keeps on looking until it finds it or hits a null pointer. However, an infinite loop could occur.
Assume capacity_ is 21, and there are two items to be inserted: item1 has a hash value equal to 41, and item2 has its hash set to 60. The location of item1 is 41 % (21 - 1) = 41 % 20 = 1. The algorithm will lookup index 1 and set the last/null Next pointer to point to item1. For item2, 60 % 20 = 0, thus, storage_[0].Next is set to point to item2; assuming Next is null. Now, if a new item comes in with a hash value of 20, 40, 21, 41 … it will point to either item1 or item2, and when it does, it will see item1 pointing to item2 and item2.Next pointing back to item1, and when it tries to find the end of the linked list, it will end up in an infinite loop.
That is fixable by storing the start address, and checking every Next variable, then break the loop if they match, then insert the new item between the last Next and the one after it (it could be null). However, there is a faster way, and that way is by adding another pointer named Anchor. Therefore, the final structure of HAItem looks like:
template <typename Key_, typename Value_>
struct HAItem {
HAItem *Anchor{nullptr};
size_t Hash{0};
HAItem *Next{nullptr};
Key_ Key{};
Value_ Value{};
};
Now Next is for collision only, and Anchor points to the location of the item. With that, Next will point to forward elements (1, 2, 3, 4, 5), and CPU prefetching may bring the next item, while the search function is comparing the given key with the current item’s Key. However, Anchor could point to anyone at that heap, and if it is null, then the item does not exist.
To understand the concept, assume that we have an array that has the capacity of 6 elements, and we need to insert the following items:
| key | Value | Hash |
item1 | A | 10 |
item2 | B | 15 |
item3 | C | 21 |
item4 | D | 24 |
The base for the hash table is (capacity – 1), which is 5. item1 is inserted in location 0 - because 10 % 5 is 0, hence, storage_[0].Anchor = the pointer of index 0. item2 is inserted at index 1, but its hash result points to 0 (15 % 5 = 0), the search function will lookup index 0 and finds item1, then it checks its Next pointer to find the final pointer that has a null value and set it to point to item2. item3 is placed in index 3, and its hash points to index 1. Even though there is an item in index 1, its Anchor is null, and the function will set storage_[1].Anchor to point to item3. item4 will get the index 3, and its hash result points to index 4, therefore, storage_[4].Anchor = &item3. And the data will look like:
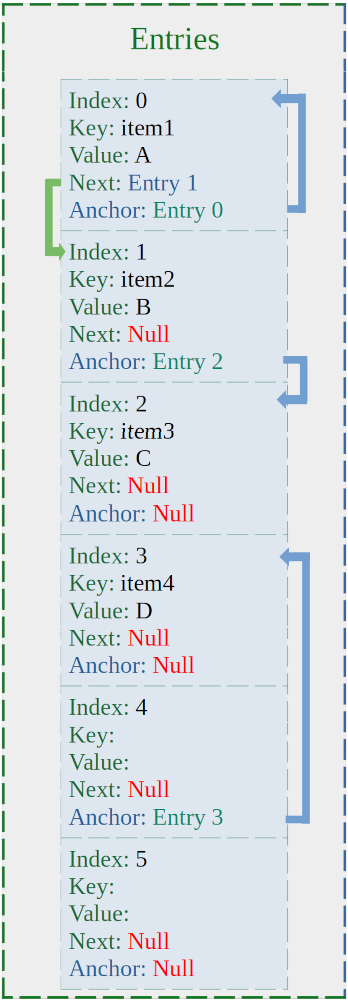
There is no need for rehashing, binary tree, separated hash table, or additional pointers. Also, having the variable Anchor means the search function can always return a reference to a pointer, and it can reference Anchor or Next, and that pointer could point to an item or null. The search function can be defined as:
public:
Value_ *Find(const Key_ &key) {
HAItem_T *item = *(find_(key, hash_fun_(key)));
if (item != nullptr) {
return &(item->Value);
}
return nullptr;
}
private:
HAItem_T **find_(const Key_ &key, size_t hash) const {
if (capacity_ == 0) {
capacity_ = 2;
storage_ = new HAItem_T[capacity_];
}
HAItem_T **item = &(storage_[(hash % capacity_)].Anchor);
while (((*item) != nullptr) && ((*item)->Key != key)) {
item = &((*item)->Next);
}
return item;
}
Hash tables check every inserted item to see if it exists or not, and with find_(), it returns a reference to that item. When it exists, it replaces its value with the given one, and if it does not, the returned reference points to where the new item should be placed in the hash table; two birds, one stone:
public:
Value_ &operator[](Key_ &&key) {
const size_t hash = hash_fun_(key);
HAItem_T **item = find_(key, hash);
if ((*item) == nullptr) {
insert_(static_cast<Key_ &&>(key), hash, item);
}
return (*item)->Value;
}
private:
void insert_(Key_ &&key, size_t hash, HAItem_T **position) {
if (index_ == capacity_) {
Resize(capacity_ * 2);
position = find_(key, hash);
}
(*position) = (storage_ + index_);
(*position)->Hash = hash;
(*position)->Key = static_cast<Key_ &&>(key);
++index_;
++size_;
}
The only time find_() is called twice, is when the size of the memory block changes; because the base depends on the value of capacity_.
public:
void Resize(size_t new_size) {
capacity_ = ((new_size > 1) ? new_size : 2);
if (index_ > new_size) {
index_ = new_size; }
const size_t base = (capacity_ - 1);
size_t n = 0;
size_t m = 0;
HAItem_T *src = storage_;
storage_ = new HAItem_T[capacity_];
while (n != index_) {
HAItem_T &src_item = src[n];
++n;
if (src_item.Hash != 0) {
HAItem_T *des_item = (storage_ + m);
des_item->Hash = src_item.Hash;
des_item->Key = static_cast<Key_ &&>(src_item.Key);
des_item->Value = static_cast<Value_ &&>(src_item.Value);
HAItem_T **position = &(storage_[(des_item->Hash % base)].Anchor);
while (*position != nullptr) {
position = &((*position)->Next);
}
*position = des_item;
++m;
}
}
index_ = size_ = m;
delete[] src;
}
Since Resize() does not need to check if the item exists or not, the rehashing mechanize is very simple (4 lines of code):
HAItem_T **position = &(storage_[(des_item->Hash % base)].Anchor);
while (*position != nullptr) {
position = &((*position)->Next);
}
*position = des_item;
The line if (src_item.Hash != 0) drops any deleted items, and deletion is the same as insertion, but it keeps track of the item that comes before the one that is going to remove; to set its Next to the Next of the next item. Also, it clears the value and the key, but keeps Next and Anchor intact; because they hold the hashing info.
public:
inline void Delete(const Key_ &key) {
delete_(key);
}
public:
void DeleteIndex(size_t index) {
if (index < index_) {
const HAItem_T &item = storage_[index];
if (item.Hash != 0) {
delete_(item.Key, item.Hash);
}
}
}
private:
void delete_(const Key_ &key, size_t hash) {
if (capacity_ != 0) {
HAItem_T **item = &(storage_[(hash % capacity_)].Anchor);
HAItem_T **before = item;
while (((*item) != nullptr) && ((*item)->Key != key)) {
before = item; item = &((*item)->Next);
}
if ((*item) != nullptr) {
HAItem_T *c_item = *item;
if ((*before) >= (*item)) {
(*before) = c_item->Next;
} else {
(*item) = c_item->Next;
}
c_item->Hash = 0;
c_item->Next = nullptr;
c_item->Key = Key_();
c_item->Value = Value_();
--size_;
}
}
}
Since HArray is an array at its heart, it is possible to add a constructor that takes an initial size:
explicit HArray(size_t size) : capacity_(size) {
if (size != 0) {
storage_ = new HAItem_T[capacity_];
}
}
Nevertheless, it is also possible to reach any key or value by an index:
Value_ *GetValue(size_t index) {
if (index < index_) {
HAItem_T &item = storage_[index];
if (item.Hash != 0) {
return &(item.Value);
}
}
return nullptr;
}
const Key_ *GetKey(size_t index) const {
if (index < index_) {
const HAItem_T &item = storage_[index];
if (item.Hash != 0) {
return &(item.Key);
}
}
return nullptr;
}
const HAItem_T *GetItem(size_t index) const {
if (index < index_) {
const HAItem_T &item = storage_[index];
if (item.Hash != 0) {
return &(item);
}
}
return nullptr;
}
Improved Implementation
While the previous implementation works and its performance is all right, there is room for improvement, starting by determining the weakest chain.
Looking at the code, the most used variable is Anchor, and it needs to be initialized even if there is no item associated with it, along with the entire structure of HAItem. Therefore, two things are needed: one, is moving Anchor to its separated data structure, and two is allocating uninitialized memory block; to avoid setting the variable twice, or not having to initialize any part of it unless it is needed. For number two, std::allocator is suitable. Therefore, the new structures are as follows:
template <typename Key_, typename Value_>
struct HAItem {
size_t Hash;
HAItem *Next;
Key_ Key;
Value_ Value;
};
struct HAItem_P {
HAItem_T *Anchor{nullptr};
};
template <typename Key_, typename Value_, typename Hash_ = std::hash<Key_>,
typename Allocator_ = std::allocator<HAItem<Key_, Value_>>>
size_t size_{0};
size_t index_{0};
size_t capacity_{0};
HAItem_P * hash_table_{nullptr};
HAItem_T * storage_{nullptr};
Allocator_ allocator_{};
};

The rest is almost the same, but since Anchor is in its separated heap, increasing its size will not affect much compared to before, and making it larger provides faster lookups and make fewer calls to Next; because of fewer collisions:
private:
void insert_(Key_ &&key, size_t hash, HAItem_T **&position) {
if (index_ == capacity_) {
Resize(capacity_ * 2);
position = find_(key, hash);
}
(*position) = (storage_ + index_);
new (*position) HAItem_T{hash, nullptr, static_cast<Key_ &&>(key), Value_{}};
++index_;
++size_;
}
private:
HAItem_T **find_(const Key_ &key, size_t hash) {
if (capacity_ == 0) {
capacity_ = 1;
hash_table_ = new HAItem_P[(capacity_ * 2)];
storage_ = allocator_.allocate(capacity_);
}
HAItem_T **item = &(hash_table_[(hash % (capacity_ * 2))].Anchor);
while (((*item) != nullptr) && ((*item)->Key != key)) {
item = &((*item)->Next);
}
return item;
}
private:
void delete_(const Key_ &key, size_t hash) {
if (capacity_ != 0) {
HAItem_T **item = &(hash_table_[(hash % (capacity_ * 2))].Anchor);
...
}
}
The resizing function can be split into two: one handles the items, the other generates the hash:
public:
void Resize(size_t new_size) {
const size_t old_capacity = capacity_;
capacity_ = ((new_size > 1) ? new_size : 2);
if (index_ > new_size) {
destruct_range_((storage_ + new_size), (storage_ + index_));
index_ = new_size; }
size_t n = 0;
size_t m = 0;
delete[] hash_table_;
HAItem_T *src = storage_;
storage_ = allocator_.allocate(capacity_);
while (n != index_) {
HAItem_T &src_item = src[n];
++n;
if (src_item.Hash != 0) {
HAItem_T *des_item = (storage_ + m);
new (des_item)
HAItem_T{src_item.Hash, nullptr,
static_cast<Key_ &&>(src_item.Key),
static_cast<Value_ &&>(src_item.Value)};
++m;
}
}
index_ = size_ = m;
allocator_.deallocate(src, old_capacity);
generate_hash_();
}
private:
void generate_hash_() {
const size_t base = (capacity_ * 2);
if (base != 0) {
hash_table_ = new HAItem_P[base];
for (size_t i = 0; i < size_; i++) {
HAItem_T *item = (storage_ + i);
HAItem_T **position = &(hash_table_[(item->Hash % base)].Anchor);
while (*position != nullptr) {
position = &((*position)->Next);
}
*position = item;
}
}
}
Improved Lookup
The remaining question now is: can it be faster? The answer is: Yes, it can be, with one simple change; replacing the division % with bitwise AND & in find_() function to be (hash & (base - 1)). The -1 is to avoid getting the size of hash table, or zeros. To understand this more, assume the size of the hash table is 4: the lookup will be 0 & 4 = 0, 1 & 4 = 0, 2 & 4 = 0, 3 & 4 = 0, but 4 & 4 = 4, which is not a valid index. Also, more zeros means more collisions. However, 1 & 3 = 1, 2 & 3 = 2, and 3 & 3 = 3, 4 & 3 = 0. Now all of them can be placed and located in the hash table.
private:
HAItem_T **find_(const Key_ &key, size_t hash) {
if (capacity_ == 0) {
base_ = 1;
capacity_ = 1;
hash_table_ = new HAItem_P[base_ + 1];
storage_ = allocator_.allocate(capacity_);
}
HAItem_T **item = &(hash_table_[(hash & base_)].Anchor);
while (((*item) != nullptr) && ((*item)->Key != key)) {
item = &((*item)->Next);
}
return item;
}
That method works well when the size can be presented as 2 to the power of N 2^n: 2, 4, 8, 16, 32, 64, 128, ... that because computers speak binary code only. Take the following table for example:
| N & (7-1) | Result |
| 0 & 6 | 0 |
| 1 & 6 | 0 |
| 2 & 6 | 2 |
| 3 & 6 | 2 |
| 4 & 6 | 4 |
| 5 & 6 | 4 |
| 6 & 6 | 6 |
0 collided with 1, 2 with 3, and 4 with 5. Now, If the size is 8, which is 2^3:
| N & (8-1) | Result |
| 0 & 7 | 0 |
| 1 & 7 | 1 |
| 2 & 7 | 2 |
| 3 & 7 | 3 |
| 4 & 7 | 4 |
| 5 & 7 | 5 |
| 6 & 7 | 6 |
No collisions! Therefore, it is O(1), but it is not that simple, because entries have keys, and the values are hashes of keys. Still, it produces fewer collisions.
Since HArry has a growth factor of 2: 1, 2, 4, 8, ... Then there is no problem using bitwise AND over making the CPU spend more time calculate, when it can be done in one operation, Well, yes, and no. Yes, if it used without initial size, and no because it has Compress(), Resize() and SetCapacity(). If it merged with another array, the sum of elements from both of them becomes the new size, if it is not less than the capacity. For that, HArry requires an additional method to align the base_:
private:
void set_base_(size_t n_size) noexcept {
base_ = 1U;
base_ <<= CLZL(static_cast<unsigned long>(n_size));
if (base_ < n_size) {
base_ <<= 1U;
}
--base_;
}
With base_ being the new variable to the class:
...
class HArray {
size_t base_{0};
size_t index_{0};
size_t size_{0};
size_t capacity_{0};
HAItem_P * hash_table_{nullptr};
HAItem_T * storage_{nullptr};
Allocator_ allocator_{};
};
For the rest:
public:
void Resize(size_t new_size) {
if (index_ > new_size) {
destruct_range_((storage_ + new_size), (storage_ + index_));
index_ = new_size; }
set_base_(new_size);
resize_(new_size);
}
private:
void resize_(size_t new_size) {
HAItem_T *src = storage_;
storage_ = allocator_.allocate(new_size);
size_t n = 0;
size_t m = 0;
while (n != index_) {
HAItem_T &src_item = src[n];
++n;
if (src_item.Hash != 0) {
HAItem_T *des_item = (storage_ + m);
++m;
new (des_item)
HAItem_T{src_item.Hash, nullptr,
static_cast<Key_ &&>(src_item.Key),
static_cast<Value_ &&>(
src_item.Value)}; }
}
index_ = size_ = m;
delete[] hash_table_;
allocator_.deallocate(src, capacity_);
capacity_ = new_size;
generate_hash_();
}
private:
void generate_hash_() {
hash_table_ = new HAItem_P[(base_ + 1)];
for (size_t i = 0; i < index_; i++) {
HAItem_T * item = (storage_ + i);
HAItem_T **position = &(hash_table_[(item->Hash & base_)].Anchor);
...
}
}
private:
void insert_(Key_ &&key, size_t hash, HAItem_T **&position) {
if (size_ == capacity_) {
++base_;
base_ *= 2;
--base_;
resize_(capacity_ * 2);
position = find_(key, hash);
}
...
}
private:
void delete_(const Key_ &key, size_t hash) {
if (capacity_ != 0) {
HAItem_T **item = &(hash_table_[(hash & base_)].Anchor);
...
}
}
For the constructor with the initial size:
explicit HArray(size_t size) : capacity_{size} {
set_base_(size);
hash_table_ = new HAItem_P[(base_ + 1)];
storage_ = allocator_.allocate(capacity_);
}
Now, it competes with the fastest.
Benchmark






Note: English words are from: https://github.com/dwyl/english-words
Compile
mkdir build
cd build
cmake -D BUILD_TESTING=0 ..
cmake --build .
./benchmark
mkdir build
cd build
cmake -D BUILD_TESTING=0 ..
cmake --build . --config Release
.\Release\benchmark.exe
mkdir build
c++ -O3 -std=c++11 -I ./include ./src/benchmark.cpp -o ./build/benchmark
./build/benchmark
Conclusion
While there are many implementations of hash tables, very few of them provide accessing elements using an index, and some of them suffer from memory fragmentation. Also, storing items in order could cause slow lookup. This implementation takes an ordered array and adds a hashing functionality to it, to make a new hash table that is fast and more usable in ~300 lines of code.
GitHub repo: https://github.com/HaniAmmar/HArray
Example
#include <iostream>
#include <string>
#include "HArray.hpp"
using Qentem::HArray;
int main() {
HArray<std::string, size_t> ha;
const size_t * val;
ha["a"] = 1;
ha["b"] = 2;
ha["c"] = 30;
ha["c"] = 3; ha["dd"] = 4;
ha["e"] = 5;
ha["z"] = 50;
ha.Rename("dd", "d");
std::cout << ha["a"] << '\n'; std::cout << ha["c"] << '\n';
std::cout << "\nSize: " << ha.Size() << "\nValues: ";
for (size_t i = 0; i < ha.ArraySize(); i++) {
val = ha.GetValue(i);
if (val != nullptr) {
std::cout << (*val) << ' '; }
}
std::cout << "\n\n";
val = ha.Find("z");
if (val != nullptr) {
std::cout << "The value of \"z\" is: " << (*val); }
std::cout << "\n\nKeys: ";
for (size_t i = 0; i < ha.ArraySize(); i++) {
const std::string *key = ha.GetKey(i);
if (key != nullptr) {
std::cout << *key << ' '; }
}
ha.Delete("z");
std::cout << "\n\nSize: " << ha.Size() << '\n'; std::cout << "Index: " << ha.ArraySize() << '\n'; std::cout << "Capacity: " << ha.Capacity() << '\n';
ha.Compress(); std::cout << "\nSize: " << ha.Size() << '\n'; std::cout << "Index: " << ha.ArraySize() << '\n'; std::cout << "Capacity: " << ha.Capacity() << '\n';
ha.Delete("d");
ha.Resize(4);
std::cout << "\nSize: " << ha.Size() << '\n'; std::cout << "Capacity: " << ha.Capacity() << "\n\n";
for (size_t i = 0; i < ha.ArraySize(); i++) {
val = ha.GetValue(i);
if (val != nullptr) {
std::cout << (*val) << ' '; }
}
std::cout << "\n\n";
ha["d"] = 4;
HArray<std::string, size_t> ha2;
ha2["b"] = 10;
ha2["d"] = 30;
ha2["w"] = 220;
ha2["z"] = 440;
HArray<std::string, size_t> ha3 = ha;
ha += ha2;
using my_item_T = Qentem::HAItem<std::string, size_t>;
for (size_t i = 0; i < ha.ArraySize(); i++) {
const my_item_T *item = ha.GetItem(i);
if (item != nullptr) {
std::cout << item->Key << ": " << item->Value << ". ";
}
}
std::cout << "\n\n";
ha2 += ha3;
for (size_t i = 0; i < ha2.ArraySize(); i++) {
const my_item_T *item = ha2.GetItem(i);
if (item != nullptr) {
std::cout << item->Key << ": " << item->Value << ". ";
}
}
std::cout << '\n';
ha.Clear();
return 0;
}
History
- 30th July, 2020: Initial version
- 3rd August 2020: Added improved implementation
- 6th August, 2020: Added improved lookup
- 10th August, 2020: Added example
