Generation of Infinite Sequences in C# and Unmanaged C++

• Download source files - 2.8 KB

Introduction

Infinite sequences, such as the Fibonacci numbers or the Prime numbers have important applications in computing. For example, Fibonacci numbers are used in some pseudo-random number generators, while one application of Prime numbers is the RSA (Rivest-Shamir-Adleman) cryptosystem. Consider the computation of the Fibonacci sequence, defined as:

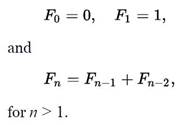
The definition is recursive and can be simply implemented in C#, say in a console application, as follows:

static int Fib( int n )
{
   if ( n <= 1 )
   {
      return n;
   }
   else
   {
      return Fib( n - 1 ) + Fib( n - 2 );
   }
}// Fib

If it were desired to keep track of all the elements of the Fibonacci sequence up to n, an alternative function would have to store them in a global array of the appropriate size. The disadvantages of such an approach are the allocation of the array and the need to know its size (or length in C#) beforehand.

Generation of a Fibonacci Sequence of Arbitrary Length in Unmanaged C++

The C and C++ programming languages allow the declaration of static local variables in functions. Such variables retain their last value between successive calls to a function that uses them. With such a facility, it is possible to define a function that will return the next Fibonacci number each time it is called, as follows:

int NextFib( int reset = 0 )
{
   static int fI = 0, fIp1 = 1;
   int retVal, nextVal;

   if ( reset )
   {
      fI = 0; fIp1 = 1;
   }
   retVal = fI;
   nextVal = fI + fIp1;
   fI = fIp1;
   fIp1 = nextVal;

   return retVal;
}// NextFib

void TestNextFib( int n )
{
   int i;

   for ( i = 0; i < n; ++i )
   {
      printf( "%d\n", NextFib() );
   }
}// TestNextFib

Function NextFib generates a sequence of Fibonacci numbers of arbitrary length, depending on the value of the argument passed to function TestNextFib.

Generation of a Fibonacci Sequence of Arbitrary Length in C#

The C# programming language DOES NOT allow the declaration of static local variables within functions. If one manages to trick the Visual Studio code editor in an attempt to declare them, the compiler issues an error.

static int NextFib( bool reset = false )
 {
    // The modifier 'static' is not valid for this item

    static int fI = 0, fIp1 = 1;
 }  // NextFib

However, the same result obtained with the unmanaged C++ code can be produced in C# by implementing a suitable IEnumerator function, as shown by the following console application:

// C:\Users\Jorge\Documents\Visual Studio 2010\Projects\C#
//   \FibStream\Program.cs
//
// Generation of sequences (streams) of Fibonacci numbers of
// arbitrary length by means of an IEnumerator function.
//
// Programmer:  Jorge L. Orejel
//
// Last update: 09/18/2020 : Removal of unnecessary 'using' statements.
//
//      01/01/2016 : Original coding.

using System;
using System.Collections.Generic;

namespace FibStream
{
   class Program
   {
      static void Main( string[] args )
      {
         Console.WriteLine();

         IEnumerator<int> Fibs = NextFib();

         for ( int i = 0; i < 40; ++i )
         {
            if ( Fibs.MoveNext() )
            {
               Console.WriteLine( "Fib( {0,2} ) = {1}",
                                  i, Fibs.Current );
            }
            else break;
         }
         Console.WriteLine();
      }// Main

      static IEnumerator<int> NextFib()
      {
         int a = 0, b = 1, t;

         while ( true )
         {
            yield return a;

            t = a + b;
            a = b;
            b = t;
         }
      }// NextFib
   }// Program (class)
}// FibStream (namespace)

The length of the sequence depends on the number of times the enumerator NextFib is called. Execution of the console application produces the following output:

Fib(  0 ) = 0
Fib(  1 ) = 1
Fib(  2 ) = 1
Fib(  3 ) = 2
Fib(  4 ) = 3
Fib(  5 ) = 5
Fib(  6 ) = 8
Fib(  7 ) = 13
Fib(  8 ) = 21
Fib(  9 ) = 34
Fib( 10 ) = 55
Fib( 11 ) = 89
Fib( 12 ) = 144
Fib( 13 ) = 233
Fib( 14 ) = 377
Fib( 15 ) = 610
Fib( 16 ) = 987
Fib( 17 ) = 1597
Fib( 18 ) = 2584
Fib( 19 ) = 4181
Fib( 20 ) = 6765
Fib( 21 ) = 10946
Fib( 22 ) = 17711
Fib( 23 ) = 28657
Fib( 24 ) = 46368
Fib( 25 ) = 75025
Fib( 26 ) = 121393
Fib( 27 ) = 196418
Fib( 28 ) = 317811
Fib( 29 ) = 514229
Fib( 30 ) = 832040
Fib( 31 ) = 1346269
Fib( 32 ) = 2178309
Fib( 33 ) = 3524578
Fib( 34 ) = 5702887
Fib( 35 ) = 9227465
Fib( 36 ) = 14930352
Fib( 37 ) = 24157817
Fib( 38 ) = 39088169
Fib( 39 ) = 63245986

Press any key to continue . . .

What is astonishing is that with the use of the yield keyword, the local variables a, b and t in NextFib behave as if they had been declared as static.

Sample Application: Dijkstra’s Classic Producer-Consumer Problem

The Producer-Consumer problem was described by the late Edsger W. Dijkstra in his chapter titled “Co-Operating Sequential Processes”, published in the book Programming Languages (edited by F. Genuys, Academic Press, 1968, pp. 43-112.) The problem involves the interaction of two processes, a producer and a consumer, that exchange items through a shared buffer in such a way that they are perfectly synchonized. For historical reasons, and in deference to the author’s former professor in the Department of Computer Sciences at the University of Texas at Austin, Dijkstra’s Algol 60 solution to the problem (on pages 71 and 72 of his chapter) is reproduced in the following figure:

The keywords begin and end enclose sequential code, the keywords parbegin and parend enclose co-operating sequential processes that run in parallel. The characters := denote the assignment statement. P (passeren in Dutch) and V (vrijeven in Dutch) are the well-known operations on mutual-exclusion or counting semaphores. They are required to be indivisible, that is, if two processes execute either of those operations on the same semaphore, the executions take place one after the other, no matter in which order.

Semaphores are data structures containing an integer value and a queue of blocked processes. Mutual-exclusion semaphores have an initial value of 1, while counting semaphores have an arbitrary positive initial value. The pseudocode for the implementation of the P and V operations is as follows:

P( S ):
   --S.value;
   if ( S.value < 0 )
   {
      Block the process that called P;
      Execute another available process;
   }

V( S ):
   ++S.value;
   if ( S.value < 0 )
   {
      Unblock the process at the front of the queue;
   }

Win32 Implementation of the Sample Application

The unmanaged C++ (Win32) implementation of Dijkstra's classic producer-consumer problem involves using two threads (one running the producer code and another running the consumer code), mutex and semaphore synchronization mechanisms, a shared buffer implemented as a circular queue, and a generator of arbitrary-length sequences of Fibonacci numbers. The producer and consumer make calls to function Sleep with different values of its argument to demonstrate that proper synchronization is independent from their relative speeds.

// C:\Users\Jorge\Documents\Visual Studio 2010\Projects\C++ unmanaged
//   \ClassicProducerConsumer\ClassicProducerConsumer.cpp
//   : Defines the entry point for the console application.
//
// Unmanaged C++ implementation of Dijkstra's classic producer/consumer
// problem using threads, mutex and semaphore synchronization mechanisms,
// a shared buffer implemented as a circular queue, and a generator of
// arbitrary-length sequences of Fibonacci numbers.
//
// Programmer:  Jorge L. Orejel
//
// Last update: 09/17/2020 : Minor cosmetic changes.
//
//      06/12/2016 : Original coding.

#include "stdafx.h"
#include <stdio.h>
#include <stdlib.h>
#include <Windows.h>

#define SIZE 10           // Circular buffer effective size.
#define SIZEp1 (SIZE + 1) // Circular buffer allocated size.
#define MAX_ITEMS 25      // Number of items to produce.
#define MAX_WAIT 15000    // Maximum wait time (15 seconds)

int buffer[ SIZE + 1 ];   // Shared buffer (one element never used).
int head, tail;           // Indices into 'buffer'.

HANDLE hMutex;            // Mutual-exclusion semaphore.
HANDLE hFull, hEmpty;     // Counting semaphores.

void InitBuffer();
int Succ( int );
void PrintBuffer();

int NextFib( int = 0 );
void TestNextFib( int );

void Producer();
void Consumer();

int _tmain( int argc, _TCHAR* argv[] )
{
   HANDLE hThreadVector[ 2 ]; // Vector for the handles to the producer/consumer threads
   DWORD threadID;

   InitBuffer();

   // Mutual-exclusion semaphore for the buffer
   hMutex = CreateMutex( NULL, FALSE, NULL );

   // Counting semaphore of full buffer slots
   hFull = CreateSemaphore( NULL, 0, (LONG)SIZE, NULL );

   // Counting semaphore of empty buffer slots
   hEmpty = CreateSemaphore( NULL, (LONG)SIZE, (LONG)SIZE, NULL );

   hThreadVector[ 0 ]
   =
      CreateThread( NULL,                             // No security attributes
                    0,                                // Default stack size
                    (LPTHREAD_START_ROUTINE)Producer, // Code executed by the thread
                    NULL,                             // No parameter passed to the thread
                    CREATE_SUSPENDED,                 // Creation flag
                    (LPDWORD)&threadID );             // Thread identifier (not used)

   hThreadVector[ 1 ]
   =
      CreateThread( NULL,                             // No security attributes
                    0,                                // Default stack size
                    (LPTHREAD_START_ROUTINE)Consumer, // Code executed by the thread
                    NULL,                             // No parameter passed to the thread
                    CREATE_SUSPENDED,                 // Creation flag
                    (LPDWORD)&threadID );             // Thread identifier (not used)

   ResumeThread( hThreadVector[ 0 ] );                // Start Producer thread
   ResumeThread( hThreadVector[ 1 ] );                // Start Consumer thread

   WaitForMultipleObjects( 2, hThreadVector, TRUE, INFINITE ); // Wait for both threads to end

   printf( "\n" );
   return 0;
}// _tmain

// Producer thread.
//
// Requirement: The Producer must be prevented from placing an item into a full buffer.

void Producer()
{
   int i, item;

   for ( i = 0; i < MAX_ITEMS; ++i )
   {
      item = NextFib(); // Produce
      Sleep( 1000 );    //   item
      WaitForSingleObject( hEmpty, MAX_WAIT ); // == P( hEmpty ): Is there an empty slot ?
      WaitForSingleObject( hMutex, MAX_WAIT ); // == P( hMutex ): Lock buffer
      //
      tail = Succ( tail );
      buffer[ tail ] = item;
      printf( "Producer: %5d -> buffer[ %2d ]: ", item, tail );
      PrintBuffer();
      //
      ReleaseMutex( hMutex );                  // == V( hMutex ): Unlock buffer
      ReleaseSemaphore( hFull, 1, NULL );      // == V( hFull):   Signal one full slot
   }
   printf( "Producer ended\n" );
}// Producer

// Consumer thread.
//
// Requirement: The Consumer must be prevented from removing an item from an empty buffer.

void Consumer()
{
   int item;

   while ( 1 )
   {
      WaitForSingleObject( hFull, MAX_WAIT );  // == P( hFull ):  Is there a full slot ?
      WaitForSingleObject( hMutex, MAX_WAIT ); // == P( hMutex ): Lock buffer
      //
      head = Succ( head );
      item = buffer[ head ];
      buffer[ head ] = -1; // Mark the slot as empty

      if ( item == -1 )          // The buffer is empty
      {                          //     because the Producer has stopped
         //
         ReleaseMutex( hMutex ); // == V( hMutex ): Unlock buffer
         break;                  // Break from the while loop
      }
      printf( "Consumer: %5d <- buffer[ %2d ]: ", item, head );
      PrintBuffer();
      //
      ReleaseMutex( hMutex );              // == V( hMutex ): Unlock buffer
      ReleaseSemaphore( hEmpty, 1, NULL ); // == V(  hEmpty ):Signal one empty slot
      Sleep( 3000 ); // Consume item
   }
   printf( "Consumer ended\n" );
}// Consumer

void InitBuffer()
{
   int i;

   for ( i = 0; i < SIZEp1; ++i )
   {
      buffer[ i ] = -1; // empty slot
   }
   head = tail = 0; // empty buffer
}// InitBuffer

int Succ( int index ) // Next index into buffer
{
   return (index + 1) % SIZEp1;
}// Succ

void PrintBuffer()
{
   int i;

   printf( "[ " );
   for ( i = 0; i < SIZEp1; ++i )
   {
      if ( buffer[ i ] == -1 )
      {
         printf( "%5c ", '.' );
      }
      else
      {
         printf( "%5d ", buffer[ i ] );
      }
   }
   printf( "]\n" );
}// PrintBuffer

// Generate next Fibonacci number
//
// From the function prototype, parameter 'reset' is
// optional, with a default value of 0.

int NextFib( int reset )
{
   static int fI = 0, fIp1 = 1;
   int retVal, nextVal;

   if ( reset )
   {
      fI = 0; fIp1 = 1;
   }
   retVal = fI;
   nextVal = fI + fIp1;
   fI = fIp1;
   fIp1 = nextVal;

   return retVal;
}// NextFib

void TestNextFib( int n )
{
   int i;

   for ( i = 0; i < n; ++i )
   {
      printf( "%d\n", NextFib() );
   }
}// TestNextFib

Execution of the preceding Win32 console application produces the following output. (Empty slots in the buffer are indicated by periods.)

Producer:     0 -> buffer[  1 ]: [     .     0     .     .     .     .     .     .     .     .     . ]
Consumer:     0 <- buffer[  1 ]: [     .     .     .     .     .     .     .     .     .     .     . ]
Producer:     1 -> buffer[  2 ]: [     .     .     1     .     .     .     .     .     .     .     . ]
Producer:     1 -> buffer[  3 ]: [     .     .     1     1     .     .     .     .     .     .     . ]
Consumer:     1 <- buffer[  2 ]: [     .     .     .     1     .     .     .     .     .     .     . ]
Producer:     2 -> buffer[  4 ]: [     .     .     .     1     2     .     .     .     .     .     . ]
Producer:     3 -> buffer[  5 ]: [     .     .     .     1     2     3     .     .     .     .     . ]
Producer:     5 -> buffer[  6 ]: [     .     .     .     1     2     3     5     .     .     .     . ]
Consumer:     1 <- buffer[  3 ]: [     .     .     .     .     2     3     5     .     .     .     . ]
Producer:     8 -> buffer[  7 ]: [     .     .     .     .     2     3     5     8     .     .     . ]
Producer:    13 -> buffer[  8 ]: [     .     .     .     .     2     3     5     8    13     .     . ]
Producer:    21 -> buffer[  9 ]: [     .     .     .     .     2     3     5     8    13    21     . ]
Consumer:     2 <- buffer[  4 ]: [     .     .     .     .     .     3     5     8    13    21     . ]
Producer:    34 -> buffer[ 10 ]: [     .     .     .     .     .     3     5     8    13    21    34 ]
Producer:    55 -> buffer[  0 ]: [    55     .     .     .     .     3     5     8    13    21    34 ]
Producer:    89 -> buffer[  1 ]: [    55    89     .     .     .     3     5     8    13    21    34 ]
Consumer:     3 <- buffer[  5 ]: [    55    89     .     .     .     .     5     8    13    21    34 ]
Producer:   144 -> buffer[  2 ]: [    55    89   144     .     .     .     5     8    13    21    34 ]
Producer:   233 -> buffer[  3 ]: [    55    89   144   233     .     .     5     8    13    21    34 ]
Producer:   377 -> buffer[  4 ]: [    55    89   144   233   377     .     5     8    13    21    34 ]
Consumer:     5 <- buffer[  6 ]: [    55    89   144   233   377     .     .     8    13    21    34 ]
Producer:   610 -> buffer[  5 ]: [    55    89   144   233   377   610     .     8    13    21    34 ]
Consumer:     8 <- buffer[  7 ]: [    55    89   144   233   377   610     .     .    13    21    34 ]
Producer:   987 -> buffer[  6 ]: [    55    89   144   233   377   610   987     .    13    21    34 ]
Consumer:    13 <- buffer[  8 ]: [    55    89   144   233   377   610   987     .     .    21    34 ]
Producer:  1597 -> buffer[  7 ]: [    55    89   144   233   377   610   987  1597     .    21    34 ]
Consumer:    21 <- buffer[  9 ]: [    55    89   144   233   377   610   987  1597     .     .    34 ]
Producer:  2584 -> buffer[  8 ]: [    55    89   144   233   377   610   987  1597  2584     .    34 ]
Consumer:    34 <- buffer[ 10 ]: [    55    89   144   233   377   610   987  1597  2584     .     . ]
Producer:  4181 -> buffer[  9 ]: [    55    89   144   233   377   610   987  1597  2584  4181     . ]
Consumer:    55 <- buffer[  0 ]: [     .    89   144   233   377   610   987  1597  2584  4181     . ]
Producer:  6765 -> buffer[ 10 ]: [     .    89   144   233   377   610   987  1597  2584  4181  6765 ]
Consumer:    89 <- buffer[  1 ]: [     .     .   144   233   377   610   987  1597  2584  4181  6765 ]
Producer: 10946 -> buffer[  0 ]: [ 10946     .   144   233   377   610   987  1597  2584  4181  6765 ]
Consumer:   144 <- buffer[  2 ]: [ 10946     .     .   233   377   610   987  1597  2584  4181  6765 ]
Producer: 17711 -> buffer[  1 ]: [ 10946 17711     .   233   377   610   987  1597  2584  4181  6765 ]
Consumer:   233 <- buffer[  3 ]: [ 10946 17711     .     .   377   610   987  1597  2584  4181  6765 ]
Producer: 28657 -> buffer[  2 ]: [ 10946 17711 28657     .   377   610   987  1597  2584  4181  6765 ]
Consumer:   377 <- buffer[  4 ]: [ 10946 17711 28657     .     .   610   987  1597  2584  4181  6765 ]
Producer: 46368 -> buffer[  3 ]: [ 10946 17711 28657 46368     .   610   987  1597  2584  4181  6765 ]
Producer ended
Consumer:   610 <- buffer[  5 ]: [ 10946 17711 28657 46368     .     .   987  1597  2584  4181  6765 ]
Consumer:   987 <- buffer[  6 ]: [ 10946 17711 28657 46368     .     .     .  1597  2584  4181  6765 ]
Consumer:  1597 <- buffer[  7 ]: [ 10946 17711 28657 46368     .     .     .     .  2584  4181  6765 ]
Consumer:  2584 <- buffer[  8 ]: [ 10946 17711 28657 46368     .     .     .     .     .  4181  6765 ]
Consumer:  4181 <- buffer[  9 ]: [ 10946 17711 28657 46368     .     .     .     .     .     .  6765 ]
Consumer:  6765 <- buffer[ 10 ]: [ 10946 17711 28657 46368     .     .     .     .     .     .     . ]
Consumer: 10946 <- buffer[  0 ]: [     . 17711 28657 46368     .     .     .     .     .     .     . ]
Consumer: 17711 <- buffer[  1 ]: [     .     . 28657 46368     .     .     .     .     .     .     . ]
Consumer: 28657 <- buffer[  2 ]: [     .     .     . 46368     .     .     .     .     .     .     . ]
Consumer: 46368 <- buffer[  3 ]: [     .     .     .     .     .     .     .     .     .     .     . ]
Consumer ended

Press any key to continue . . .

Using the Code

There are two files containing the code. The file Program.cs is the C# source code to generate sequences of Fibonacci numbers of arbitrary length. The file ClassicProducerConsumer.cpp is the Win32 implementation of Dijkstra’s solution to the producer-consumer problem.

History

• 20^th September, 2020: Initial version