Data-Driven Model Predictive Controller (MPC) in Simulink Matlab

Introduction

This article implements a data-driven model predictive controller (MPC) in the Simulink Matlab. The controller utilizes the on-line data that are given from the original system and the desired signals. In fact, the controller tries to reach the system's output to the desired signal by evaluating the control input. The control input is the output of the controller that is applied to the original system. Thus, the controller has two inputs and one output ports which are the system's output, desired reference signal, and the control input, respectively. The controller is implemented in a Simulink subsystem that its parameters can be easily modified through double-clicking on the subsystem and inserting the desired controller's parameters which are presented in the following.

The developed subsystem fits an ARIMA model on the real system's outputs and inputs. Then, an MPC is applied to the on-line estimated ARIMA model for the control aim. The main control aim is to reach the system's outputs to the desired reference signals. In the following, the developed subsystem is shown:

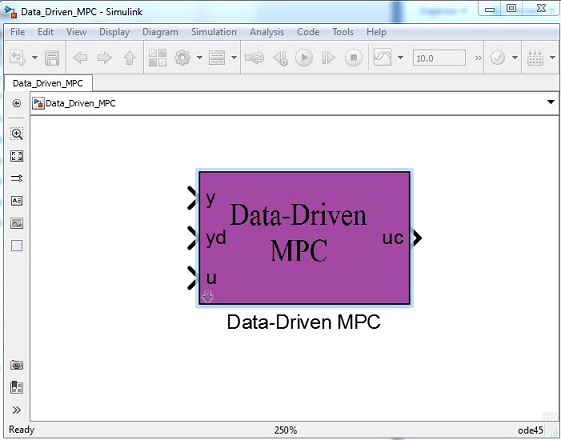
The developed subsystem as shown in the above picture can be directly used by connecting its ports into the original system that is desired to be controlled.

Background

As stated earlier, the developed Simulink subsystem simultaneously implements an online model fitting and model predictive controller (MPC). In the first step, an ARIMA model is considered as follows:

y(t)=A1*y(t-1)+A2*y(t-2)+...+Ap*y(t-p)+B1*u(t-1)+B2*u(t-2)+...+Bq*u(t-q)

where y(t) and u(t) are the outputs and inputs of the original system. Parameters mu and my stand for the numbers of the outputs and inputs of the original system. Also, parameters p and q are the orders of the ARIMA model which are used in the above equation. These parameters can be manually modified by changing them in the parameters of the subsystem. The developed subsystem fits a model like the above one on the inputs and outputs of the original system which its internal properties are supposed to be fully unknown.

In the second step, an appropriate MPC is applied to the obtained ARIMA model. The controller attempts to reach the system's outputs y(t) to the desired reference signals yd(t) by properly designing the control sequence based on the idea of MPC. The controller parameters involving the prediction and control horizons are denoted by Ny and Nu in the developed subsystem. In fact, the controller predicts the system's output y(t) in the future steps as given below:

y(t+1)=A1*y(t)+A2*y(t-1)+...+Ap*y(t-p+1)+B1*U(t)+B2*u(t-1)+...+Bq*u(t-q+1)

y(t+2)=A1*y(t+1)+A2*y(t)+...+Ap*y(t-p+2)+B1*U(t+1)+B2*U(t)+B3*u(t-1)...+Bq*u(t-q+2)

...

y(t+Ny)=A1*y(t+Ny-1)+A2*y(t+Ny-2)+...+Ap*y(t+Ny-p)+B1*U(t+Ny-1)+B2*U(Ny-2)+...

Then, the controller precisely determines the control sequence U=[U(t) U(t+1) ... U(t+Nu-1)] such that the prediction outputs Y=[y(t+1) y(t+2) ... y(t+Ny)] closes to the reference signals yd(t). For this purpose, an optimization problem is defined and solved to optimally determine the control sequence U. The optimum control sequence is obtained at each step t and its first entry is applied to the original system as the control input.

It should be noted that the developed subsystem can be used for both SISO and MIMO systems. It means the systems may have more than one output and input ports.

Using the Code

In this subsection, some explanatory notes about the utilization of the developed subsystem are given in some examples.

In the first example, assume it is desired to control the LTI system 1/(s+1) to follow a sine-wave reference signal as shown in the following picture:

The above picture simply describes how the developed controller can be used in the Simulink. For this purpose, the original system (that is 1/(s+1)) is implemented and its output is connected to the "y" port of the Data-Driven MPC and the "uc" port of the data-driven MPC is connected to its input. The desired reference signal is considered as a sine-wave that its parameters can be modified. Then, the controller tries to close the output signal of the original system into the desired signal.

By clicking on the Data-Driven MPC, the following properties are shown:

Some of the above parameters are previously defined and the others are defined here. Parameter "T" stands for the time step. Parameters "umin", "umax" and "udmax" represent the minimum, maximum, and the time-derivative maximum of the control input signal, respectively. All of these parameters can be changed due to the limits of the original system. In the sequel, the system's output and its desired signal are shown to evaluate the performance of the controller:

As can be seen, the controller properly controls the system.

In the second example, the data-driven MPC is applied to a water-tank system to control its level. The details of this example is given in Example2.slx in the attached file and it is shown here:

The desired Water Level is set at 2 and the Data-Driven MPC is exploited of this control aim. The controller can be easily used without any information about the internal of the original system which is a Water-Tank system in this example. The parameters of the controller can be adjusted based on the operator limits and commands. The following figure shows the appropriate tracking of the system's output signal:

The above figure reveals the ability of the implemented controller to control the Water Level in this example.

The developed subsystem utilizes a script which is noted by myfun that simulates both online estimation and MPC design. The code is given in the following:

//
function Z=myfun(y,yref,u,t,umin,umax,udmax,p,q,my,mu,Ny,Nu,T,th0,P0)
global U Y P th Uo yh;
U=[U(2:end,:);u'];
if t==0      
    P=P0;th=th0;
    U=zeros(q,mu);Y=zeros(p,my);
    Uo=zeros(Nu,mu);    
end
H=zeros(my,my^2*p+my*mu*q);
ind=1;
for i=1:p
    H(:,ind:ind+my^2-1)=kron(Y(p-i+1,:),eye(my));ind=ind+my^2;
end
for i=1:q
    H(:,ind:ind+my*mu-1)=kron(U(q-i+1,:),eye(my));ind=ind+my*mu;
end
H=H';
m=size(H,2);
L=(P*H)/(eye(m)+H'*P*H);
P=P-L*H'*P;
th=th+L*(y'-H'*th);
yh=zeros(my,1);
for i=1:p
    ind=1+(i-1)*my^2;
    Ai=reshape(th(ind:ind+my*my-1),my,my);
    yh=yh+Ai*Y(p-i+1,:)';
end
for i=1:q
    ind=1+p*my^2+(i-1)*my*mu;
    Bi=reshape(th(ind:ind+my*mu-1),my,mu);
    yh=yh+Bi*U(q-i+1,:)';
end
Y=[Y(2:end,:);y'];
umin=reshape(umin,length(umin),1);
umax=reshape(umax,length(umax),1);
udmax=reshape(udmax,length(udmax),1);
G=zeros(Ny*my,Nu*mu);g=zeros(Ny*my,1);
for i=1:Ny
    Ge=zeros(my,size(G,2));ge=zeros(my,1);
    for j=1:p
        ind=1+(j-1)*my^2;
        Aj=reshape(th(ind:ind+my*my-1),my,my);
        if j>=i
            ge=ge+Aj*Y(end-j+i,:)';
        else
            Gw=G((i-j-1)*my+1:(i-j)*my,:);
            gw=g((i-j-1)*my+1:(i-j)*my,:);
            Ge=Ge+Aj*Gw;
            ge=ge+Aj*gw;
        end
    end
    for j=1:q
        ind=1+p*my^2+(j-1)*my*mu;
        Bj=reshape(th(ind:ind+my*mu-1),my,mu);
        if j>i
            ge=ge+Bj*U(end-j+i+1,:)';
        elseif i-j+1<=Nu
            Ge(:,(i-j)*mu+1:(i-j+1)*mu)=Ge(:,(i-j)*mu+1:(i-j+1)*mu)+Bj;
        end
    end
    G((i-1)*my+1:i*my,:)=Ge;
    g((i-1)*my+1:i*my,:)=ge;
end
z1=ones(Nu,1);
if ~isempty(udmax)
    A1=eye(Nu*mu);b1=Uo+T*kron(z1,udmax);
    A2=-eye(Nu*mu);b2=-Uo+T*kron(z1,udmax);
    A=[A1;A2];b=[b1;b2];
else
    A=[];b=[];
end
if ~isempty(umin)
    Umin=kron(z1,umin);
else
    Umin=[];
end
if ~isempty(umax)
    Umax=kron(z1,umax);
else
    Umax=[];
end
Yref=kron(ones(Ny,1),yref);
gb=g-Yref;
opt=optimset('disp','none');
Uo=quadprog(2*(G'*G),2*G'*gb,A,b,[],[],Umin,Umax,Uo,opt);
uc=Uo(1:mu);
Z=[uc;yh];
end
//

The above code is internally used in the developed subsystem that explains how the data-driven MPC is implemented.

Points of Interest

This Simulink subsystem can be easily used by inserting it into any control loops. This subsystem can be used in the scientific articles as a comparative controller to evaluate the performance of your developed controller.

History

• 18^th October, 2020: Initial version