Finding the Convex Hull of Multi-Dimensional Points in C

• Download source - 5.6 KB

Introduction

Finding the convex hull of some given points is an intermediate problem in some engineering and computer applications. For example, the convex hull must be used to find the Delaunay mesh of some points which is significantly needed in 3D graphics. Thus, this article focuses on this topic and develops a library for solving the mentioned problem in C language. The C language is utilized due to its applicability to be implemented in the basic platforms.

One of the most important properties of the provided library is its ability to be used for 2D, 3D, and higher dimensional points. Some previous cases of the convex hull codes can be only used for 2D or 3D points while the supplied library can be used for the higher ones.

The library exploits the quick hull algorithm to find the convex hull that is fully implemented in this code. It should be noted that a group of algorithms is developed for solving this problem which among them, the quick hull algorithm is more popular and better.

The supplied code can be easily used by including the header file in your modules which is the other advantage of the code. It must be emphasized that the coordinations of the points are imported to code via a CSV file and the results (facets) are exported by the other CSV files that are entirely explained in the rest of this article.

Background

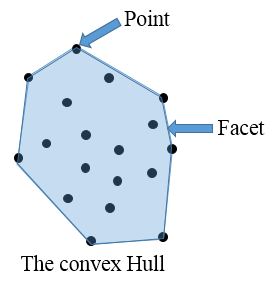
This section presents some basics and backgrounds that are used in this article. The first is the convex hull that is the smallest convex space containing the given points. In fact, finding the convex hull is the problem of determining the smallest convex space that contains the points which are given as the problem's input. The smallest convex space is represented through a set of facets. The next image explains these definitions for a better understanding:

As stated earlier, the quick hull algorithm is exploited in the supplied code which is directly given from this link, which may be useful for more details about the algorithm.

This paper presents the following quick hull algorithm for finding the convex hull of some points with d the dimension that is presented by the next image. (Please, note that the algorithm is directly given the paper without any modification):

Moreover, a matrix library is needed to derive the resulting in which some basic matrix algebra operations are implemented. For this purpose, the following matrix library is exploited:

• Matrix Library in C

Now, the supplied library is presented in the next section.

Convex Hull Library

At first, it should be noted that a C struct is used for the convex hull library that is given in the following code block:

struct convexhull{
	Mat* facets;
	Mat* neighbors_indices;
	Mat* outpoints_indices;
	Mat* points;	
	Mat* center;
	int dim;
};

In the above struct, points is a matrix that includes the primary given points, center is the center of these points, and dim is the points' dimension.

Furthermore, facets, neighbors_indices, and outpoints_indices are respectively the facets, their neighbor facets indices, and the indices of the outside points of each facet that are finally obtained by the code. In fact, these matrices are outputs of the code that can be used to show the obtained convex hull. The matrix facets shows the facets of the final convex hull, neighbors_indices presents the indices of the facets that are located at the neighborhood of each facet (i^th row contains the neighbor facets of the i^th facet), and outpoints_indices contains the indices of the points that lie outside each facet (i^th row contains the indices of points that are outside i^th facet). According to the convex hull algorithm, the algorithm terminates whenever all facets do not have any outside points. Thus, this matrix will be empty at the end of the algorithm.

The input points are imported through a CSV file that contains all points' coordinations such as given in the following:

0.1138,-1.2119
0.9299,2.1966
-2.3492,3.0224
2.001,0.91613
-3.0714,1.374
-4.1366,3.381
-2.6511,-3.9353
1.6579,0.59524
-2.1934,-1.7031
4.6641,2.8957

Indeed, each row contains the coordinations of one specific point. Therefore, the input points should be set as the above template to be used by the code. The code is able to export the final facets matrix that represented the convex hull of the given points. The facets are given in a CSV file that is presented in the next section.

The main code of the supplied library is convh() that is given here:

convexhull* convh(Mat* points){
	int dim=points->col;
	int Np=points->row;
	convexhull* cvh=(convexhull*)malloc(sizeof(convexhull));
	cvh->points=points;cvh->dim=dim;	
	init(cvh);	
	while(1==1){				
		int i=1;
		while(i<=cvh->facets->row&&cvh->outpoints_indices->entries[(i-1)*Np]==0){
			i++;
			continue;
		}		
		if(i>cvh->facets->row){
			break;
		}
		int fp=furthestpoint(cvh,i);				
		Mat* local_facets=newmat(1,0,0);
		Mat* boundary_facets=newmat(1,0,0);
		int Nf1=cvh->facets->row;
		localsearch(cvh,local_facets,boundary_facets,i,0,fp);		
		updatenewfacets(cvh,local_facets,boundary_facets,Nf1);									
		freemat(local_facets);
		freemat(boundary_facets);		
	}
	return cvh;
}

As can be seen, function convh() gives the primary points and obtains their convex hull struct that contains the result. Assume file1.txt is the CSV file that includes the points. Then, the above function can be simply called as given here:

int _tmain(int argc, _TCHAR* argv[])
{
	Mat* V=readmat("file1.txt");
	showmat(V);
	convexhull* cvh=convh(V);
	writemat("file2.txt",cvh->facets);
	writemat("file3.txt",cvh->neighbors_indices);
	writemat("file4.txt",cvh->outpoints_indices);
	getchar();
	return 0;
}

In the following, two examples are presented that show the results of applying the above code in two 2D and 3D problems. First, consider a set of 2D points which are visually presented by the following figure:

And, the obtained convex hull is given in the next figure:

Now, the above example is repeated for 3D points with the following given points:

The convex hull of the above points are obtained as follows by the code:

As can be seen, the code correctly obtains the convex hull of the 2D and 3D points. It must be emphasized that the code is capable to be used for the higher dimensional points which cannot visually show here.

Using the Code

The developed library can be easily used by including the following header files.

//
# include "MatLib.h"
# include "convexhull.h"
//

Points of Interest

The article implements the quick hull algorithm for finding the convex hull of the multi-dimensional points. The code is implemented in C language that can be used in basic platforms.

History

• 30^th October, 2020: Initial version