Here we will introduce the basics of machine learning (ML) for readers with no knowledge of AI, and we will describe the training and verification steps in supervised ML models.
ML is a branch of AI that tries to get machines to figure out how to perform a task by generalizing from a set of examples instead of receiving explicit instructions. There are three paradigms of ML: supervised learning, unsupervised learning, and reinforcement learning. In supervised learning, a model (which we will talk about below) learns through a process known as training, where it is provided with example inputs and their correct outputs. It learns what features from the dataset examples map to specific outputs and is then able to predict new incoming data in a phase known as prediction. In unsupervised learning, models learn the structure of data by analyzing the relations between them without having any other process involved. In reinforcement learning, we build models that learn and improve over time by means of trial and error techniques.
What is a model in ML? A model is simply a mathematical object or entity that contains some theoretical background on AI to be able to learn from a dataset. Popular models in supervised learning include decision trees, support vector machines, and of course, neural networks (NNs).
NNs are arranged in layers in a stack kind of shape. The nodes in each layer except for the input and output layers receive inputs from nodes in the previous layer and can also receive inputs from nodes in the following layer, and likewise can send signals, or outputs, to nodes in the previous and next layer.
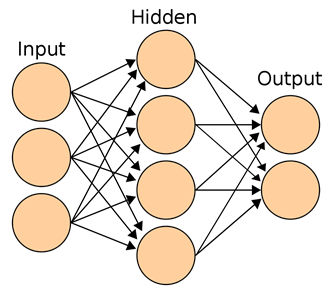
In a NN we always have input and output layers, and we may have one or more hidden layers. The simplest NN is the perceptron, which contains only an input layer and an output layer of a single node.
For each edge in the NN there is an associated weight, and for each node there is an associated value. The value of each node in the input layer could, for example, come from the input array of pixel values associated with an image in a dataset. In order to calculate what the value of a node in the next layer will be, we calculate the weighted sum of inputs connected to that node. This is known as the transfer function. Once this value is calculated, it is passed to another function known as the activation function, which determines whether this node should fire to the next layer or not based on a threshold. Some activation functions are binary and some others can have multiple outputs.

Usually at the end of a NN we have an activation function that classifies (makes a decision about) the data passed into the input layer. In the case of coin recognition, it would decide the class or type of coin in the image. The learning process in a NN can be seen merely as an adjustment of its weights so that we obtain the expected output for each given input. Once a model has been trained, the resulting weights can be saved.
Whenever a NN has more than one hidden layer, it is considered deep learning (DL). DL is a set of techniques that rely on NNs having more than one hidden layer. The reason for having more than one hidden layer is to provide more accurate results than what a single hidden layer NN would provide. It has been proven that DL can produce much quicker results and be more accurate than those of a single hidden layer NN. Plus, each layer you add to your NN aids in learning complicated features from a dataset.
NNs contain many parameters that need to be adjusted for better performance. To be able to check the validity of our parameter tuning and the performance of the NN itself, we set aside a large portion of the original dataset (usually greater than 70 percent) to use as a training set, use the rest as a validation (testing) set. The validation set also helps us prevent overfitting, which occurs when a model learns too well a set of very similar objects in the dataset, making it too fit for this data and unfit for new data that varies a bit from the original examples.
In the next article, we will examine a convolutional neural network for the problem of coin recognition, and we will implement one in Keras.NET.
