Using Bottom Up Dynamic Programming to Solve the Coin Change Problem

Today we are going to demonstrate how to use Top Down Dynamic Programming to solve the problem, Coin Change.

If you want to learn how to solve a problem with the Top Down approach, there’s another article we wrote that looked at solving the Climbing Stairs problem using Top Down DP.

Understanding the Problem

In Coin Change, we are given an array of coins of different value and starting value that we want to make change for. The goal is to find the minimum number of coins needed to give the exact change.

With an example problem of coins = [2,3, 5] and change = 7. We can see all the possible combinations of coins that we can give.

We can see that there are 2 paths that lead to answer of 2 coins used:

One thing to note is that we repeat the calculation for certain amounts of changes. Specifically change=1 and change=2. If our change value was larger we would have found larger amounts of duplicate and this is when DP comes to the rescue!

High Level Algorithm

DP is a technique that allows us to cache answers of sub-problems to repeat making the same calculations over and over.

Unlike the previous article we will solve this problem using the bottom up approach.

The bottom-up approach, as opposed to the top down approach builds our solution starting from the base case. We start from the smallest sub-problem that we know the answer to and we continue trying to solve upward until we know the answer to the problem.

Starting from the very bottom, the smallest sub-problem that we know change = 0. This is the base case.

We use an array to store the answer to these sub-problems with the goal of reaching change = 7.

Let’s try to solve the problem change=1.

Remember in the graph that showed  the possible path, we didn’t draw it out, because we couldn’t make any change, but to find the minimum number of coins to give for change=1, we would try and see what happens if we used all 3 given coins (2,3, and 5)

To calculate the answer, we to know the minimum number of coins used to make change(1-2), change(1-3), and change(1-5), which in this instance are all negative, so there’s no way to make change for 1, when we have coins worth 2,3, and 5

Let’s move on to try the subproblem change=2.

If we try to use all 3 coins, we would see that we can use the 2 coins to give us perfect change at change=2, specifically at our base. The other two coins would give us a negative amount so we will skip them.

It takes 0 coins to make change for 0. We would take 0 and add the 1 coin we use to make change from 2, giving us our minimum of 1 coin used to make change for 2.

For change=3, we do something similar as we did at change=2

Coin 2 and 5 gives us invalid change, however using coin 3, we can use 1 coin to make change for 3.

At change=4, something interesting happens. Using coin 3 and 5 would not lead us to any valid answers, however coin 2, will lead us to change=2. 

In a bruteforce situation, we would try to calculate the minimum number of coins to make change for 2. Luckily because we are going from the bottom up, we already made and saved the minimum number of coins used for change=2, which is 1.

We take that answer and we add 1 to it because we used the 2 coin to give change at 4, giving us our answer of using 2, 2 coins to give change for 4

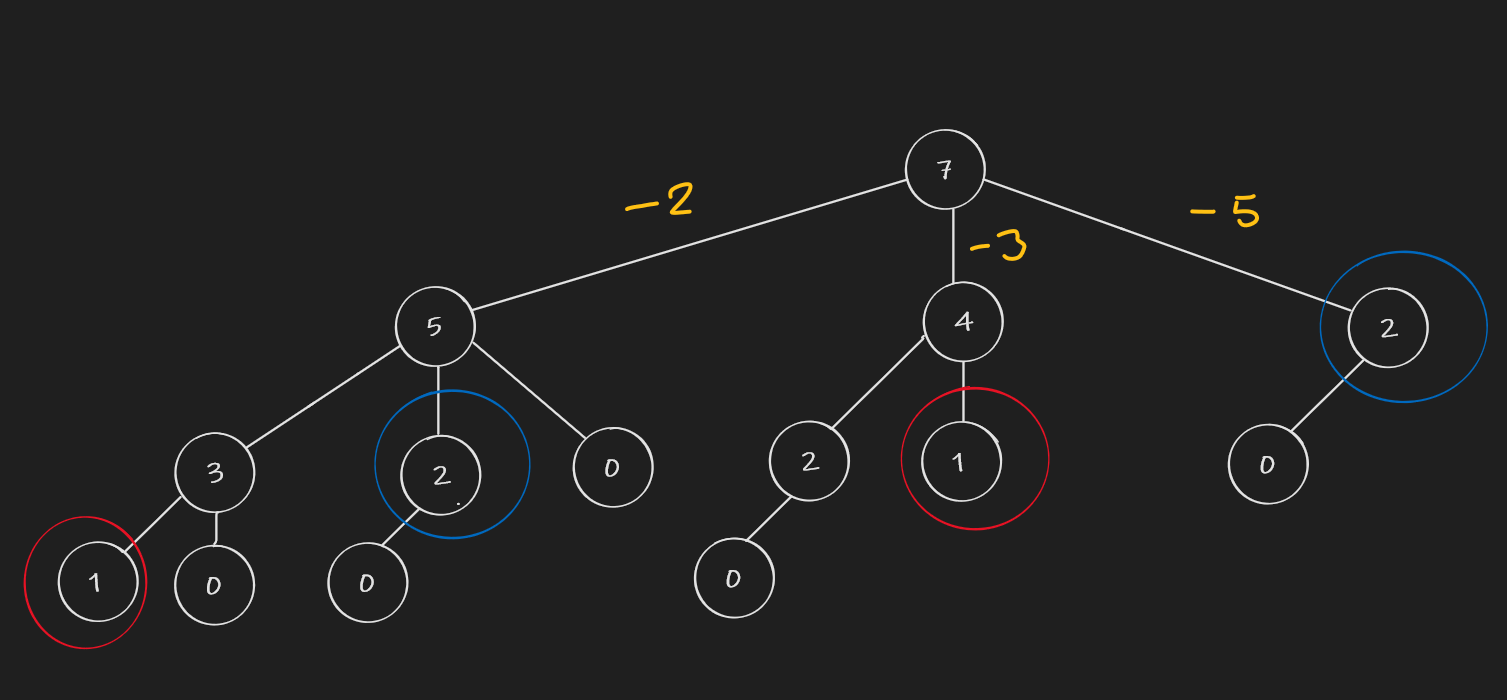
Moving on, at change=5, we can finally use all 3 coins to make change.

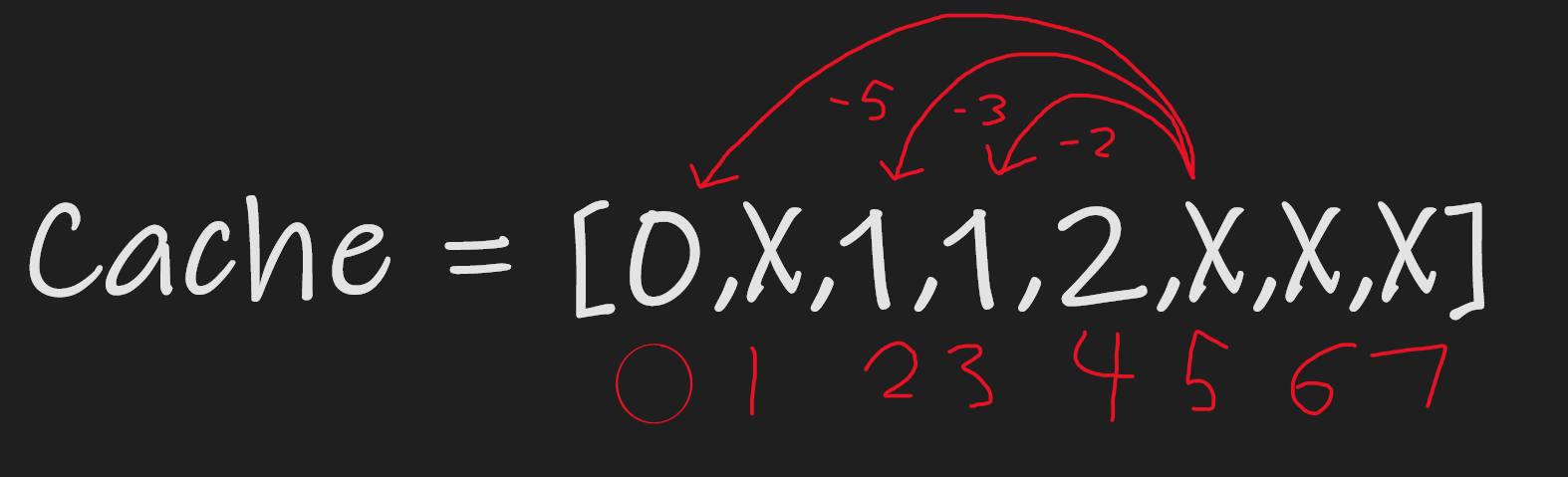
At this point, hopefully we see a pattern, where we use the previously calculated value of cache[change-coin] + 1, to figure out the coins used. However in this instance, we have 3 numbers to compare:

• Coin 2 give us 2 coins used
• Coin 3 give us 2 coins used
• Coin 5 give us 1 coin used

We take the minimum number of coins used and store it in our array.

We follow the same pattern for change=6

And finally change=7, the answer that we are looking for:

After having gone through all change numbers, we know now that the minimum number of coins used to give perfect change is 2.

You might have noticed that for this algorithm we followed a specific mathematical equation to calculate the minimum number of coins used.

For example, if we want to find change=5, our algorithm did:

change(5) = min(change(5-2), change(5-3), change(5-5)) + 1

We can generalize this to:

change(n) = min(change(n-2), change(n-3), change(n-5)) + 1

In the academic world, this is called a recurrence relation which is an equation used to find an answer to a problem by finding the answer to a sub-problem.

Another way of thinking of the recurrence relation in regards to the top down approach is that it is our recursive case.

Being able to break down a problem to smaller subproblems and caching value is the key to these DP problems. 

Having experienced writing recursion, I personally have an easier time thinking about DP problems from a Top down approach, however both are valid and offer the same runtime complexities, there might be certain cases where bottom-up might be able to only use constant space to solve the problem.

In general, if you’re like me, the general approach I like to use to solve a DP problem is to solve it Top-down first and then reuse the logic to solve it from bottom-up:

1. Solve the problem using a Brute force recursive solution
2. Solve the problem using top-down memoization
3. Take the base case, recursive case, and our cache to build up a solution from the bottom-up

Just like with the top down approach, the hard part of solving any DP problem is not actually DP itself, it’s being able to solve the problem with recursion (or figure out the recurrence relation).

Runtime and Space Complexity

Runtime

The runtime of this algorithm requires two things:

• N = The amount of change that we want to give
• M = The number of coins that we are given

In our algorithm for all N value, we need to find the minimum number of coins used for all M value, this would give us the runtime of O(N*M)

Space Complexity

The spacetime is O(N), where we made an array to store the calculation for all change from 0 to N

Implementation

class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] cache = new int[amount + 1];
        for (int i = 1; i <= amount; i++) {
            // We are looking for the minimum value, we initialize 
            // the value to be the largest value it can be + 1 as a
            // maximum
            int minCoins = amount + 1;
            for (int coin : coins) {
                int remain = i - coin;
                // If the coin would give us negative change, we
                // will skip it
                if (remain < 0) {
                    continue;
                }
                // We find the minimum number of coins used in
                // remain, otherwise it'll stay at the same value
                minCoins = Math.min(minCoins, cache[remain] + 1);
            }
            cache[i] = minCoins;
        }
        
        // Finally, if the answer to our problem is our max value, we know
        // that there must not have been an answer and return -1, otherwise
        // we return the minimum number of coins used
        return cache[amount] == amount + 1 ? -1 : cache[amount];
    }
}

Conclusion

The key lesson from solving the Coin Change problem with the bottom-up approach is to figure out the base case and the recursive case (recurrence relation) and then building up your answer starting from the base case.

There is generally no difference between solving a problem using top-down vs bottom-up, however there are certain advantages to solving problems using the bottom-up approach:

• You could optimize for space depending on the problem
• The code is generally shorter

Besides these 2 points, you can pick whatever strategy you are most confident in and implement your solution!

The post Using Bottom Up Dynamic Programming to Solve the Coin Change Problem appeared first on Leet Dev.