Predicting Near Term COVID Death Rates

Introduction

The COVID Tracking Project publishes a daily, curated data set of global COVID cases, hospitizations, deaths and other data points. Reporting in the US seems to focus on lagging indicators like cases reported and fatalities-to-date. So using the Tracking Project's data, let's see the correlation between cases and future fatalities. As you might expect, there is a reliable relationship between the two.

• Source code and daily results

Using the code

Python and Jupyter notebooks are great tools for experimentation and visualization of this sort of thing. Pandas, numpy, matplotlib and SKLearn provide more than enough functionality for a straightforward analysis.

startDate = np.datetime64('2020-06-24') # the earliest date in the data to use 
country = 'USA' # the country code to analyse

# load and filter the dataset to just the locale and period of interest
raw_data = pd.read_csv('https://covid.ourworldindata.org/data/owid-covid-data.csv', 
           usecols=['date', 'iso_code', 'new_deaths', 'new_cases', 'new_deaths_smoothed', 
           'new_cases_smoothed'], parse_dates=['date'])
df = raw_data[(raw_data.iso_code == country) & (raw_data.date >= startDate) &
    (~raw_data.new_deaths.isnull()) &
    (~raw_data.new_cases.isnull()) &
    (~raw_data.new_deaths_smoothed.isnull()) &
    (~raw_data.new_cases_smoothed.isnull())]
df.info()

After some initial exploration of the dataset for the US, it is pretty clear that there is a linear relationship between cases and deaths. From there, it's relatively straightforward to offset the case data from the fatalities by several days and find the offset with the best r².

Model = namedtuple('Model', 'linearRegression r2 offset data')

def BestFitModel(new_cases, new_deaths, max_offset) -> Model:
    best = Model(None, 0.0, 0, None)

    # find an offset, in days, where cases best correlate to future deaths
    for offset in range(1, max_offset):
        cases = new_cases[-0:-offset]
        deaths = new_deaths[offset:]

        model = LinearRegression().fit(cases, deaths)
        predictions = model.predict(cases)
        r2 = metrics.r2_score(deaths, predictions)
        if (r2 > best.r2):
            best = Model(model, r2, offset, 
                         pd.DataFrame({'predicted': predictions, 'actual': deaths}))

    return best

Results

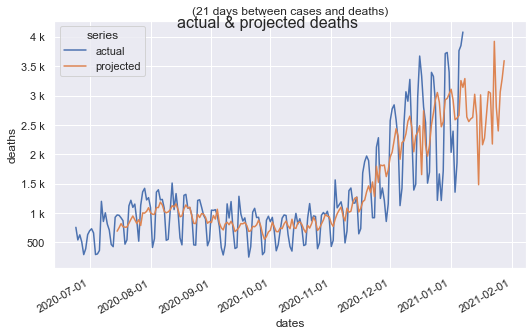
Reporting noise (weekends and holidays get under-reported) and are very spikey. Even with that noise, the data shows a strong correlation somewhere between 14 and 21 days offset. It's almost always a factor of 7 because of the weekend pattern.

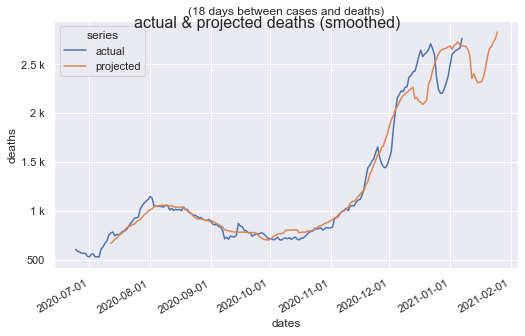
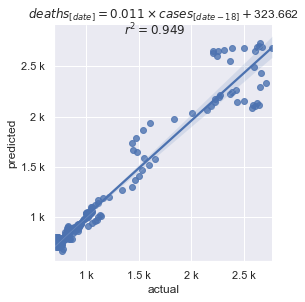
Smoothed data points, included in the Tracking Project's data set, removes the weekend pattern, but under-reporting over Thanksgiving and Christmas remain. Despite that, correlation is > 0.94.

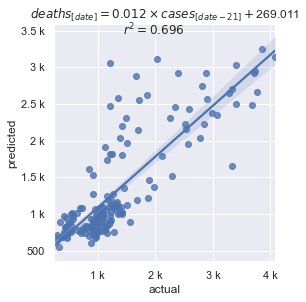
Once the best fitting linear equation is found, it's straight forward to predict the number of deaths for the next number of days, equal to the offset used to find that equation.

def Predict(model: Model, dates, cases, deaths) -> pd.DataFrame:
    # create a new date series for the range over which we will predict
    # (it is wider than the source date range by [offset]. 
    #  That is how far in the future we can predict)
    minDate = np.amin(dates)
    maxDate = np.amax(dates) + np.timedelta64(model.offset + 1, 'D')

    projected_dates = [date for date in np.arange(minDate, maxDate, dt.timedelta(days=1))]

    # padding so actuals and predictions can be graphed together within dates
    padding = pd.Series(np.full(model.offset, np.nan))

    actual_deaths = deaths.append(padding)
    projected_deaths = padding.append(pd.Series(model.linearRegression.predict(cases)))

    frame = pd.DataFrame({"dates": projected_dates, 
        "actual": actual_deaths.values, 
        "projected": projected_deaths.values}, index=projected_dates)

    # unpivot the data set for easy graphing
    return frame.melt(id_vars=['dates'], var_name='series', value_name='deaths')

Points of Interest

For the curious, the results are updated and published to GitHub each day.

History

• 2^nd January, 2021 - Initial release