This article provides a simple C++ class without any complications in the mathematical calculations of the backpropagation algorithm. Two use cases have been provided to facilitate code usage.
Contents
Background
This article is not to explain the scientific side of (ANN) Artificial Neural Networks. It provides a simple C++ class without any complications in the mathematical calculations of the backpropagation algorithm. If you have good experience about ANN, you can skip to the next section, else, you can revise this very good resources about ANN. I have provided two use cases to facilitate code usage as much as possible.
Introduction
Today, (ANN) Artificial neural networks has become dominant in many areas of life, whether an industry or at home. ANN enables machines to learn and to simulate human brain to recognize patterns, and make predictions as well as solve problems in every business sector. Smartphones and computers that we use on a daily basis are using ANN in some of its applications. For example, Finger Print and Face unlock services in smartphones and computers use ANN. Handwritten Signature Verification uses ANN. I have written a simple implementation for an Artificial Neural Network C++ class that handles backpropagation algorithm. The code depends on Eigen open-source templates to handle Matrices’ mathematics. I made code simple and fast as possible.
NeuralNetwork Class
NeuralNetwork is a simple C++ class with the following structure:
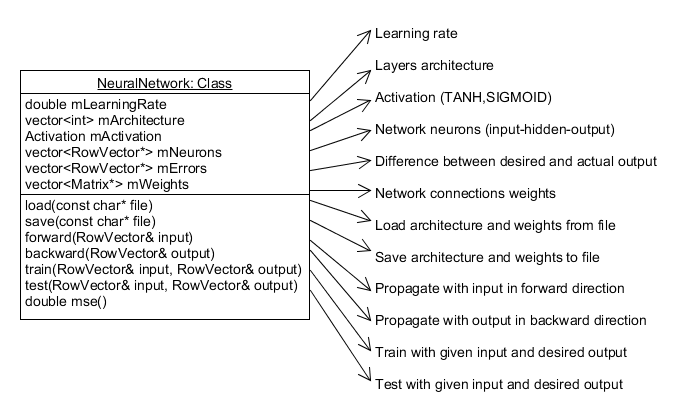
The code uses RowVectorXd and MatrixXd from Eigen template library. The main functions "train" and "test" take input and desired output in RowVector format. Both of them call "forward" function which uses vector multiplication.

forward
void NeuralNetwork::forward(RowVector& input) {
mNeurons.front()->block(0, 0, 1, input.size()) = input;
for (unsigned int i = 1; i < mArchitecture.size(); i++) {
mNeurons[i]->block(0, 0, 1, mArchitecture[i]) =
(*mNeurons[i - 1] * *mWeights[i - 1]).block(0, 0, 1, mArchitecture[i]);
for (int col = 0; col < mArchitecture[i]; col++)
mNeurons[i]->coeffRef(col) = activation(mNeurons[i]->coeffRef(col));
}
}
The function propagates with input through network layers to get output from the last layer. Each neuron in the hidden layer first computes a weighted sum of its inputs. Then it applies an activation function (segmoid) to this sum to derive its output. This function affects neurons values only. It doesn't affect connections weights or errors. This function does this sum with vector multiplication:
(*mNeurons[i - 1] * *mWeights[i - 1])
Then, resultant values are passed through activation function.
double NeuralNetwork::activation(double x) {
if (mActivation == TANH)
return tanh(x);
if (mActivation == SIGMOID)
return 1.0 / (1.0 + exp(-x));
return 0;
}
tanh

sigmoid

backward
void NeuralNetwork::backward(RowVector& output) {
*mErrors.back() = output - *mNeurons.back();
for (size_t i = mErrors.size() - 2; i > 0; i--)
*mErrors[i] = *mErrors[i + 1] * mWeights[i]->transpose();
size_t size = mWeights.size();
for (size_t i = 0; i < size; i++)
for (int col = 0, cols = (int)mWeights[i]->cols(); col < cols; col++)
for (int row = 0; row < mWeights[i]->rows(); row++) {
mWeights[i]->coeffRef(row, col) +=
mLearningRate *
mErrors[i + 1]->coeffRef(col) *
activationDerivative(mNeurons[i + 1]->coeffRef(col)) *
mNeurons[i]->coeffRef(row);
}
}
The function is key of the Backpropagation algorithm. It takes output of last layer and propagates backward through network layers, calculates each layer errors, and update connections weights depending on the rule:
new weight = old weight + learingRate * next error * sigmoidDerivative(next neuron value)
double NeuralNetwork::activationDerivative(double x) {
if (mActivation == TANH)
return 1 - tanh(x) * tanh(x);
if (mActivation == SIGMOID)
return x * (1.0 - x);
return 0;
}
tanh derivative

sigmoid derivative

Note: The curve of sigmoidDerivative has a big significance. As its input ranges from 0 to 1 (neuron value), there are the three possible cases:
- neuron value near
0, so weight value doesn't need support.

- neuron value near
0.5, so weight value needs a slight change.

- neuron value near
1, so weight value doesn't need support.

train
void NeuralNetwork::train(RowVector& input, RowVector& output) {
forward(input);
backward(output);
}
The function propagates input in forward direction, then propagates backward with the resultant output to adjust connections weight.
test
void NeuralNetwork::test(RowVector& input, RowVector& output) {
forward(input);
*mErrors.back() = output - *mNeurons.back();
}
The function propagates input in forward direction, then calculates error between resultant output and desired output.
evaluate
There are various ways to evaluate the performance of neural network model, such as Confusion matrix, Accuracy, Precision, Recall, and F1 score. I have added “Confusion Matrix” calculation to the code through the evaluate function call after each testing call.
void NeuralNetwork::evaluate(RowVector& output) {
double desired = 0, actual = 0;
mConfusion->coeffRef(
vote(output, desired),
vote(*mNeurons.back(), actual)
)++;
}
This function simply fill the right cell in the confusion matrix depending on the match between the actual and desired output.
After the hole testing the confusion matrix can be used to calculate Precision, Recall, and F1 score.
void NeuralNetwork::confusionMatrix(RowVector*& precision, RowVector*& recall) {
int rows = (int)mConfusion->rows();
int cols = (int)mConfusion->cols();
precision = new RowVector(cols);
for (int col = 0; col < cols; col++) {
double colSum = 0;
for (int row = 0; row < rows; row++)
colSum += mConfusion->coeffRef(row, col);
precision->coeffRef(col) = mConfusion->coeffRef(col, col) / colSum;
}
recall = new RowVector(rows);
for (int row = 0; row < rows; row++) {
double rowSum = 0;
for (int col = 0; col < cols; col++)
rowSum += mConfusion->coeffRef(row, col);
recall->coeffRef(row) = mConfusion->coeffRef(row, row) / rowSum;
}
...
}
This calclation will be clear in the second Usecase Handwritten Digits Recognition
Use Cases
Simple Counter

Neural network takes an input in binary (3 bits) and generates an output equals to input + 1. Then output is taken back as an input to the network. If input number equals to 7 (111 in binary) output should be 0. Network is trained using backpropagation algorithm to adjust network's connections weights. Training process takes about 2 minutes to minimize error between desired output and actual network output.
| Input | Output |
| 0 0 0 | 0 0 1 |
| 0 0 1 | 0 1 0 |
| 0 1 0 | 0 1 1 |
| 0 1 1 | 1 0 0 |
| 1 0 0 | 1 0 1 |
| 1 0 1 | 1 1 0 |
| 1 1 0 | 1 1 1 |
| 1 1 1 | 0 0 0 |

Simply, construct NeuralNetwork class with the required architecture and learningRate.
NeuralNetwork net({ 3, 5, 3 }, 0.05, NeuralNetwork::Activation::TANH);
3 neurons in input layer, 5 neurons in hidden layer, and 3 neurons in output layer.
0.05 learning rate.
The following figure describes full training process for the network with 50,000 trials.

Train Network
void train(NeuralNetwork& net) {
cout << "Training:" << endl;
RowVector input(3), output(3);
int stop = 0;
for (int i = 0; stop < 8 && i < 50000; i++) {
cout << i + 1 << endl;
for (int num = 0; stop < 8 && num < 8; num++) {
input.coeffRef(0) = (num >> 2) & 1;
input.coeffRef(1) = (num >> 1) & 1;
input.coeffRef(2) = num & 1;
output.coeffRef(0) = ((num + 1) >> 2) & 1;
output.coeffRef(1) = ((num + 1) >> 1) & 1;
output.coeffRef(2) = (num + 1) & 1;
net.train(input, output);
double mse = net.mse();
cout << "In [" << input << "] "
<< " Desired [" << output << "] "
<< " Out [" << net.mNeurons.back()->unaryExpr(ptr_fun(unary)) << "] "
<< " MSE [" << mse << "]" << endl;
stop = mse < 0.1 ? stop + 1 : 0;
}
}
}
The function takes a network with an architecture { 3, 5, 3 } and does 50000x8 training call till it reaches acceptable error margin. After each training call, it displays input, output, and desired output.
- In the first stages of training, the MSE (mean square error) is large, and output is so far from desired output.

- After many rounds of training, the MSE decreased, and output came closer to desired output.

- Finally, after 788 rounds, the MSE became less than 0.1 and the output was close to desired output.

Test Network
void test(NeuralNetwork& net) {
cout << "Testing:" << endl;
RowVector input(3), output(3);
for (int num = 0; num < 8; num++) {
input.coeffRef(0) = (num >> 2) & 1;
input.coeffRef(1) = (num >> 1) & 1;
input.coeffRef(2) = num & 1;
output.coeffRef(0) = ((num + 1) >> 2) & 1;
output.coeffRef(1) = ((num + 1) >> 1) & 1;
output.coeffRef(2) = (num + 1) & 1;
net.test(input, output);
double mse = net.mse();
cout << "In [" << input << "] "
<< " Desired [" << output << "] "
<< " Out [" << net.mNeurons.back()->unaryExpr(ptr_fun(unary)) << "] "
<< " MSE [" << mse << "]" << endl;
}
}
This function tests some inputs with the pre-trained network. It prints resultant output and MSE.

Save Network
int main() {
NeuralNetwork net({ 3, 5, 3 }, 0.05);
RowVector input(3), output(3);
train(net, input, output);
test(net, input, output);
net.save("params.txt");
return 0;
}
After training and testing network, we can save network structure in a file to be loaded later for network usage without retraining.
For our case, resultant file contains:
learningRate: 0.05
architecture: 3,5,3
activation: 0
weights:
-1.34013 0.811848 0.314629 1.85447 -0.343212 0.151176
0.98971 -0.684254 1.20649 0.260128 -6.50245 -2.31706
0.702027 -3.15824 -0.80735 1.07841 -2.57619 -2.17761
0.13025 3.17894 0.594173 -3.18092 -0.0574412 -2.39394,
-2.67379 0.467493 0.403606
-1.22918 1.67581 1.60877
1.1605 -1.95284 0.942444
-1.92978 -0.704029 -1.12284
-1.34765 -2.8206 1.44205
-0.996246 -1.52939 0.205469
The first line in weights section represents weights between first neuron in input layer and all neurons of next layer:
-1.34013 0.811848 0.314629 1.85447 -0.343212 0.151176

The second line in weights section represents weights between second neuron in input layer and all neurons of next layer:
0.98971 -0.684254 1.20649 0.260128 -6.50245 -2.31706

and, so on ...
Handwritten Digits Recognition
Handwritten recognition is one of the most successful application for Artificial Neural Network. It is the "Hello world" application for Neural Network study. In the previous use case, I use a shallow neural network, which has three layers of neurons that process inputs and generate outputs. Shallow neural networks can handle equally complex problems. But, in Handwritten Recognition, we need more accuracy and nonlinearity. Therefore, I have to use Deep Neural Network (DNN). DNN has two or more hidden layers of neurons that process inputs.
Network Architecture
Using a network architecture {784, 64, 16, 10} (input - two hidden layers - output), I have achieved a success of 93.16%.

Activity Diagram
The following figure illustrates activity diagram of the whole process.

Used Libraries
This project uses:
- MNIST dataset for network training and testing. You have to download MNIST dataset files and put them in project execution path.
- libpng library for PNG files reading. You can download libpng16 (lib - h) files and put it in project build path.
- zlib library used internally by libpng16 to decompress images.
MNIST dataset contains 60,000 training images of handwritten digits from zero to nine and 10,000 images for testing. So, the MNIST dataset has 10 different classes. The handwritten digits images are represented as a 28×28 matrix where each cell contains grayscale pixel value (0 to 1).

Training and Testing
During training and testing, digit is read from its PNG file and converted from 28x28 image to a 784 double value of gray scale. This vector represented the input to the input layer of the neural network.
void readPng(const char* filepath, RowVector*& data) {
pngwriter image;
image.readfromfile(filepath);
int width = image.getwidth(); int height = image.getheight(); data = new RowVector(width * height);
for (int y = 0; y < height; y++)
for (int x = 0; x < width; x++)
data->coeffRef(0, y * width + x) = image.dread(x, y);
}

The following figure describes full training and testing processes for the network with 60,000 images (50,000 training - 10,000 testing).

- In the first stages of training, error is large and the output is so far from the desired output.

- After many rounds of training, the MSE decreased and the output came closer to the desired output.

- After testing 10000 images:

- Display Training and Testing Cost and error percentage:

Save Network
int main() {
.......
if (!testOnly)
net.save("params.txt");
return 0;
}
After training and testing network, we can save network structure in a file to be loaded later for network usage without retraining. If you are going to retrain, you have to delete the file "params.txt" from build path.
For our case resultant file contains:
learningRate: 0.05
architecture: 784,64,16,10
activation: 1
weights:
-0.997497 -0.307718 -0.0558184 0.124485 -0.188635 0.557909 0.242286
-0.898618 -0.942442 0.355693 0.284951 0.100192 0.724357 -0.998474
0.763909 -0.127537 0.893246 -0.956969 -0.492111 -0.775506 -0.603442
-0.907712 -0.987793 -0.0556963 -0.510117 0.450484 0.644276 0.951292
0.105869 -0.76458 0.586596 0.480819 0.253029 -0.672964 -0.418134
0.117222 0.121494 0.439985 -0.459639 -0.514145 0.458296 0.639027
-0.926817 -0.581164 0.774529 -0.392315 -0.985656 0.405133 -0.0527665
-0.0163884 -0.00704978 0.138768 -0.2219 -0.927671 -0.880856 0.977355
-0.927854 0.253273 -0.154149 -0.877621 0.797845 0.388653 0.0682699
0.3361 -0.108066
0.127171 -0.962889 0.39848 -0.457381 0.470931 -0.574816 -0.820429
-0.851558 -0.925108 0.224769 0.575488 0.975402 -0.688955 0.78692
0.0274972 -0.218848 -0.790765 0.708121 0.144139 -0.574694 0.749809
0.781732 0.362285 -0.662099 -0.903134 0.375225 0.581286 -0.679678
0.0863369 0.295511 -0.418195 0.241249 -0.720573 -0.794733 0.0434278
-0.81109 0.895749 0.652699 0.970824 0.643422 -0.0625935 0.776421
-0.656117 0.23075 -0.18247 -0.250649 -0.197546 0.621632 0.804376
-0.976745 0.178747 0.137059 -0.404828 -0.564013 -0.309915 -0.376385
-0.66924 0.245216 -0.3961 0.160741 0.364788 0.150121 -0.811396
-0.837397 -0.901669
....
Evaluation
After testing the network we can calculate evaluation items Precision, Recall, and F1 score from the Confusion Matrix.
Precision is the ratio between correct recognition (true positive) to predicted digit.
Precision = (0.95+0.97+0.95+0.95+0.92+0.93+0.96+0.95+0.94+0.89)/10 = 94%
Recall is the ratio between correct recognition (true positive) to actual digit.
Recall = (0.98+0.98+0.93+0.93+0.92+0.94+0.93+0.94+0.92+0.92)/10 = 94%
void evaluate(NeuralNetwork& net) {
RowVector* precision, * recall;
net.confusionMatrix(precision, recall);
double precisionVal = precision->sum() / precision->cols();
double recallVal = recall->sum() / recall->cols();
double f1score = 2 * precisionVal * recallVal / (precisionVal + recallVal);
cout << "Confusion matrix:" << endl;
cout << *net.mConfusion << endl;
cout << "Precision: " << (int)(precisionVal * 100) << '%' << endl;
cout << *precision << endl;
cout << "Recall: " << (int)(recallVal * 100) << '%' << endl;
cout << *recall << endl;
cout << "F1 score: " << (int)(f1score * 100) << '%' << endl;
delete precision;
delete recall;
}
The resultant values are like that:
Confusion matrix:
98.6735 0.102041 0 0.102041 0 0.204082 0.306122 0.306122 0.306122 0
5.659e-313 98.2379 0.264317 0.176211 0 0 0.264317 0.176211 0.792952 0.0881057
1.06589 0.290698 93.5078 0.387597 1.45349 0.290698 0.484496 1.16279 0.968992 0.387597
0 0.29703 1.18812 93.5644 0.0990099 1.48515 0.29703 0.990099 0.891089 1.18812
0.101833 0 0.407332 0.101833 92.9735 0 0.916497 0.203666 0 5.29532
0.44843 0.112108 0.112108 2.01794 0.336323 94.2825 0.44843 0.560538 1.00897 0.672646
1.46138 0.313152 0.417537 0 1.04384 2.71399 93.6326 0.104384 0.313152 0
0 1.07004 1.16732 0.194553 0.583658 0.194553 0 94.5525 0.0972763 2.14008
0.616016 0.513347 0.616016 1.12936 1.12936 0.718686 0.821355 0.821355 92.4025 1.23203
0.99108 0.396432 0 0.891972 3.07235 0.396432 0.099108 0.693756 0.49554 92.9633
Precision: 94%
0.95459 0.972949 0.958292 0.951662 0.922222 0.934444 0.961415 0.951076 0.948367 0.895893
Recall: 94%
0.986735 0.982379 0.935078 0.935644 0.929735 0.942825 0.936326 0.945525 0.924025 0.929633
F1 score: 94%
We can visualize the confusion matrix in the following table:

This table shows how often the model classified each digit correctly in blue, and which digits were most often confused for that label in gray.
History
- 24th January, 2021: Initial post
- 7th March, 2021: Evaluate model with Confusion Matrix
