This article describes a C# program to implement McCarthy’s ambiguity (amb) operator and its use in the implementation of ambiguous functions and a non-deterministic function.
Introduction
The late John McCarthy published a paper titled “A Basis for a Mathematical Theory of Computation”, included in the book Computer Programming and Formal Systems, edited by P. Braffort and D. Hirshberg and published by North-Holland in 1963. In that paper, McCarthy discussed, among many other aspects of computation, ambiguous functions.
Ambiguous Functions
McCarthy stated that ambiguous functions are not really functions because for each combinations of values of its arguments, an ambiguous function returns a list of possible values. He posed as an example the function less( n ) defined for all positive integer values of n. The function is ambiguous because every non-negative integer less than n is a possible value of less( n ). In order to define this function, McCarthy defined a basic ambiguity operator amb( x, y ) whose possible values are x and y when both are defined; otherwise, whichever is defined. Observe that, according to its basic definition, the ambiguity operator returns a list of values. (This will change later on.) The function less( n ) can be defined in terms of the amb operator as follows:
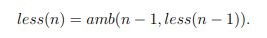
Due to the nature of his paper, after this definition, McCarthy did not provide any implementation details. (A cautionary note: lest the reader jump to the conclusion that McCarthy was just a pure mathematician, it must be recalled that he not only designed and implemented the first version of the Lisp programming language, but also invented the concept of time-sharing, which is the basis for the implementation of any modern operating system.)
Implementation of the amb Operator
From this point onward, all the C# code to be shown will be assumed to reside within the context of a Visual Studio console application.
A fundamental property of the amb operator is that the value it returns depends on whether or not its arguments are defined. The way to handle this property in C# is by using nullable types, which are scalar types that can take null as their value. (Nullable types were introduced in C# so that programs could handle NULL values from, say, SQL Server databases.) With this in mind, the amb operator can be implemented as follows:
static List<int> amb( int? x, int? y )
{
List<int> values = new List<int>();
if ( x != null && y != null )
{
values.Add( (int)x );
values.Add( (int)y );
}
else
{
if ( x != null )
{
values.Add( (int)x );
}
else if ( y != null )
{
values.Add( (int)y );
}
}
return values;
}
In the code above, int? is an integer nullable type. The amb function returns a list of integers and it is a straightforward implementation of the semantics of the amb operator. However, there is a catch.
From McCarthy’s definition of ambiguous function less( n ), it is not difficult to see that, in general, the second argument to the amb operator may be a list of values (which may be null) and not just a scalar nullable type. To handle this situation, function amb may be overloaded as follows:
static List<int> amb( int? x, List<int> y )
{
List<int> values = new List<int>();
if ( x != null && y != null )
{
values.Add( (int)x );
values.AddRange( y );
}
else
{
if ( x != null )
{
values.Add( (int)x );
}
else if ( y != null )
{
values = y;
}
}
return values;
}
The changes with respect to the first version of the function have to do with handling the second argument when it is a list, namely values.AddRange( y ) and values = y.
Implementation of Ambiguous Functions
With the functionality for the amb operator given above, the ambiguous function less( n ) can be implemented as follows:
static List<int> less( int n )
{
return n == 0
? null
: amb( n - 1, less( n - 1 ) );
}
Another ambiguous function similar to less( n ) is a function dealing with powers of 2. Given a value n as the exponent of 2, all the positive powers of 2 less than 2n are possible values of the following function.
static List<int> ltPof2( int n )
{
return n == 0
? null
: amb( 1 << ( n - 1 ), ltPof2( n - 1 ) );
}
Testing the Preceding Code
Putting all the code into a Visual Studio console application, the functionality of the amb operator and of the two ambiguous functions can be tested within the main program, as in the following example:
static void Main( string[] args )
{
PrintList( " amb( 5, 7 )", amb( 5, 7 ) );
PrintList( " amb( null, 7 )", amb( null, 7 ) );
PrintList( " amb( 5, (int?)null )", amb( 5, (int?)null ) );
PrintList( "amb( (int?)null, (int?)null )", amb( (int?)null, (int?)null ) );
Console.WriteLine();
PrintList( "less( 10 )", less( 10 ) );
PrintList( " less( 2 )", less( 2 ) );
PrintList( " less( 0 )", less( 0 ) );
Console.WriteLine();
PrintList( "ltPof2( 10 )", ltPof2( 10 ) );
PrintList( " ltPof2( 2 )", ltPof2( 2 ) );
PrintList( " ltPof2( 0 )", ltPof2( 0 ) );
Console.WriteLine();
}
Where function PrintList simply displays a list of values on the console.
static void PrintList( string operation, List<int> list )
{
Console.Write( "\n{0}: [", operation );
if ( list != null )
{
foreach ( int i in list )
{
Console.Write( " {0}", i );
}
}
Console.WriteLine( " ]" );
}
Execution of the sample main program produces the results shown in the following figure:

Resolution on the Function Value
Once an ambiguous function returns a list of possible values, the issue that arises is which of those values is to be used as the value of the function for further processing. The answer is simple: if the list of possible values contains more than one element, just pick one value from the list at random. The changes that would have to be made could be as follows:
static Random rnd;
static void Main( string[] args )
{
rnd = new Random();
PrintListAndResolve( "less( 10 )", less( 10 ) );
PrintListAndResolve( "less( 10 )", less( 10 ) );
PrintListAndResolve( " less( 2 )", less( 2 ) );
PrintListAndResolve( " less( 0 )", less( 0 ) );
Console.WriteLine();
}
static void PrintListAndResolve( string operation, List<int> list )
{
Console.Write( "\n{0}: [", operation );
if ( list != null )
{
foreach ( int i in list )
{
Console.Write( " {0}", i );
}
}
Console.Write( " ] " );
int n = list == null ? 0 : list.Count;
if ( n == 0 )
{
Console.WriteLine( " no resolution" );
}
else
{
Console.Write( " resolved to: " );
if ( n == 1 )
{
Console.WriteLine( "{0}", list[ 0 ] );
}
else
{
int index = rnd.Next( 0, n - 1 );
Console.WriteLine( "{0}", list[ index ] );
}
}
}
The execution of the modified Main function would produce results like the following. (Due to the use of a random number generator, the results will vary.)
less( 10 ): [ 9 8 7 6 5 4 3 2 1 0 ] resolved to: 4
less( 10 ): [ 9 8 7 6 5 4 3 2 1 0 ] resolved to: 1
less( 2 ): [ 1 0 ] resolved to: 1
less( 0 ): [ ] no resolution
Press any key to continue . . .
With the resolution action, the amb operator now returns a single value.
Nullable amb
A nullable version of amb receives several arguments and returns one of them “ambiguously”, that is, at random. The function returns either one of the arguments or null and can be implemented as follows:
public static IEnumerator<int?> amb( params int?[] args )
{
int n = args == null ? 0 : args.Length;
List<int> chosen = new List<int>();
if ( n == 0 )
{
yield return null;
}
else
{
while ( chosen.Count < n )
{
int index = rnd.Next( 0, n );
if ( !chosen.Contains( index ) )
{
chosen.Add( index );
yield return args[ index ];
}
}
yield return null;
}
}?>
Then the following two functions can be used to test the nullable version of amb.
static void TestNullableAmb( params int?[] args )
{
int n = args == null ? 0 : args.Length;
List<int?> arglist = args.ToList<int?>();
Console.WriteLine( "\nTestNullableAmb:\n" );
Console.Write( "amb( " );
if ( n > 0 )
{
for ( int i = 0; i < n; ++i )
{
Console.Write( "{0} ", NintToString( arglist[ i ] ) );
}
}
IEnumerator<int?> Amb = Fn.amb( args );
Amb.MoveNext();
Console.WriteLine( ") ==> {0}", NintToString( Amb.Current ) );
while ( Amb.MoveNext() )
{
Console.WriteLine( "amb() ==> {0}", NintToString( Amb.Current ) );
}
}
static string NintToString( int? i )
{
return i == null
? "null" : i.ToString();
}
The following two figures show the results obtained from several calls to function TestNullableAmb. Again, due to the use of a random number generator, in general, the results will be different.


Continuous amb
All the versions of amb implemented so far eventually return null. In preparation for the discussion of a very interesting application of amb, two continuous versions of amb that never return null are as follows:
public static IEnumerator<string> amb2( params string[] args )
{
int n = args == null ? 0 : args.Length;
if ( n == 0 )
{
yield return null;
}
else
{
while ( true )
{
int index = rnd.Next( 0, n );
yield return args[ index ];
}
}
}
public static IEnumerator<string> amb3( params string[] args )
{
int n = args == null ? 0 : args.Length;
if ( n == 0 )
{
yield return null;
}
else
{
int index;
while ( true )
{
index = rnd.Next( 0, n );
RotateArgs( args, n );
yield return args[ index ];
}
}
}
static void RotateArgs( string[] args, int n )
{
string _1stArg = args[ 0 ];
for ( int i = 0, j = 1; j < n; ++i, ++j )
{
args[ i ] = args[ j ];
}
args[ n - 1 ] = _1stArg;
}
Application of amb to the Four-Color Problem
At least as of 1977, the four-color problem, or conjecture, “has been one of the greatest unsolved problems in mathematics” (T.L. Saaty and P.C. Kainen, The Four-Color Problem: Assaults and Conquest, McGraw-Hill 1977, p. 3.) The problem was posed by Francis Guthrie about 167 years ago and its statement is rather simple: given an arbitrary map, is it possible to color it with at most four colors in such a way that countries sharing a border (i.e., neighbouring countries) do not have the same color? The answer, in the affirmative, to the conjecture was found by Wolfgang Haken and Kenneth Appel in 1976, and it required more than a thousand hours of computer time, that is, the “proof” was not mathematical. (See R. Wilson, Four Colors Suffice, Princeton University Press 2014, p. 3.)
Previous computer-based solutions of the four-color problem have been implemented in Prolog (see L. Sterling and E Shapiro, The Art of Prolog, The MIT Press 1986, pp. 212-214, 53, and 114) and in the Scheme dialect of the Lisp programming language (see D. Sitaram, “Teach Yourself Scheme in Fixnum Days”, section 14.4.2). The Prolog program is iterative while the Scheme program is recursive and uses success and failure continuations. Both programs are non-deterministic. Recall that, given the same input, a non-deterministic program returns different results on different runs. The results may be the same on two or more runs but, in general, the results must be expected to differ.
In this section, the amb operator will be used to tackle the four-color problem by means of a non-deterministic C# function to color the countries of western Europe. The function will not rely on backtracking. Using wishful thinking, the C# code will be developed in a top-down fashion. The complete code consisting of files Program.cs, Country.cs and Fn.cs is in the attached ZIP file.
From this point onward, the code shown will be assumed to reside within the namespace AmbiguousFunctions in a console application. First, there must be a way to represent countries and information related to them. A country will have a name, a color, an instance of an amb operator over an array of four colors, a set of neighbors and a set of neighbors colors. Observe that the use of the amb operator makes the color assignment non-deterministic.
static string[] colors = { "red", "yellow", "blue", "white" };
public class Country
{
public string Name;
public string Color;
private IEnumerator<string> Amb;
private HashSet<Country> neighbors;
private HashSet<string> neighborsColors;
public Country( string name, params string[] colors )
{
Name = name;
Amb = Fn.amb3( colors );
Amb.MoveNext();
Color = Amb.Current;
neighbors = new HashSet<Country>();
neighborsColors = new HashSet<string>();
}
}
The string representation of a country consists of its name and its color.
public override string ToString()
{
return String.Format( "{0,12}: {1} ",
Name,
Color == String.Empty ? "null" : Color );
}
Once all the countries have been created (instantiated), their neighbors data member can be populated.
public void SetNeighbors( params Country[] countries )
{
foreach ( Country country in countries )
{
neighbors.Add( country );
}
}
A country is assigned a color for the first time (upon instantiation of the Country class) or its color can be re-assigned after its neighborsColors data member is filled with the colors of its neighbors.
public bool AddToNeighborsColors( params Country[] countries )
{
foreach ( Country country in countries )
{
neighborsColors.Add( country.Color );
}
return this.AssignColor();
}
public bool AssignColor()
{
bool assigned = false;
int i = 0;
do
{
Amb.MoveNext();
++i;
if ( Amb.Current != Color )
{
Color = Amb.Current;
}
} while ( neighborsColors.Contains( Color ) && i < 4 );
if ( i < 4 )
{
assigned = true;
}
return assigned;
}
The last function member of class Country generates a string containing the names and colors of the neighbors of a country.
public string NeighborsColorsToString()
{
StringBuilder sb = new StringBuilder();
int i = 0;
sb.Append( "\n\t\t " );
foreach ( Country neighbor in neighbors )
{
sb.Append( String.Format( " [{0}: {1}]", neighbor.Name, neighbor.Color ) );
++i;
if ( i > 2 )
{
sb.Append( "\n\t\t " );
i = 0;
}
}
sb.Append( "\n" );
return sb.ToString();
}
With the functionality of class Country in place, the code in Program.cs can now be developed. The Main function creates an instance of a random-number generator class and initiates the map-coloring process by calling function ColorWesternEurope.
static Random rnd;
static void Main( string[] args )
{
rnd = new Random();
ColorWesternEurope();
Console.WriteLine();
}
static void ColorWesternEurope()
{
Console.WriteLine( "\nColorWesternEurope:\n" );
CreateCountries();
SetNeighbors();
ShowColors();
FillNeighborsColors();
ShowCountriesAndNeighbors();
}
static void CreateCountries()
{
portugal = Countries[ (int)CountryEnum.Portugal ]
= new Country( "Portugal", colors );
spain = Countries[ (int)CountryEnum.Spain ]
= new Country( "Spain", colors );
france = Countries[ (int)CountryEnum.France ]
= new Country( "France", colors );
belgium = Countries[ (int)CountryEnum.Belgium ]
= new Country( "Belgium", colors );
holland = Countries[ (int)CountryEnum.Holland ]
= new Country( "Holland", colors );
germany = Countries[ (int)CountryEnum.Germany ]
= new Country( "Germany", colors );
luxembourg = Countries[ (int)CountryEnum.Luxembourg ]
= new Country( "Luxembourg", colors );
italy = Countries[ (int)CountryEnum.Italy ]
= new Country( "Italy", colors );
switzerland = Countries[ (int)CountryEnum.Switzerland ]
= new Country( "Switzerland", colors );
austria = Countries[ (int)CountryEnum.Austria ]
= new Country( "Austria", colors );
}
Once the countries of western Europe are instantiated, their neighbors data members are filled and the initial color assignments are displayed.
static void SetNeighbors()
{
portugal.SetNeighbors( spain );
spain.SetNeighbors( france, portugal );
france.SetNeighbors( spain, italy, switzerland,
belgium, germany, luxembourg );
belgium.SetNeighbors( france, holland, luxembourg, germany );
holland.SetNeighbors( belgium, germany );
germany.SetNeighbors( france, austria, switzerland, holland,
belgium, luxembourg );
luxembourg.SetNeighbors( france, belgium, germany );
italy.SetNeighbors( france, austria, switzerland );
switzerland.SetNeighbors( france, italy, austria, germany );
austria.SetNeighbors( italy, switzerland, germany );
}
static void ShowColors()
{
Console.WriteLine( "Initial colors:\n" );
foreach ( CountryEnum country in Enum.GetValues( typeof( CountryEnum ) ) )
{
Console.WriteLine( Countries[ (int)country ].ToString() );
}
Console.WriteLine();
}
Then comes the task of filling the neighborsColors data member of each country. After that is done, each country’s color is re-assigned if necessary. If the color of a country cannot be re-assigned, a failure message is displayed.
static void FillNeighborsColors()
{
Console.WriteLine( "\nFillNeighborsColors:\n" );
if ( !portugal.AddToNeighborsColors( spain ) )
{
Failure( portugal );
}
if ( !spain.AddToNeighborsColors( france, portugal ) )
{
Failure( spain );
}
if ( !france.AddToNeighborsColors( spain, italy, switzerland,
belgium, germany, luxembourg ) )
{
Failure( france );
}
if ( !belgium.AddToNeighborsColors( france, holland, luxembourg, germany ) )
{
Failure( belgium );
}
if ( !holland.AddToNeighborsColors( belgium, germany ) )
{
Failure( holland );
}
if ( !germany.AddToNeighborsColors( france, austria, switzerland, holland,
belgium, luxembourg ) )
{
Failure( germany );
}
if ( !luxembourg.AddToNeighborsColors( france, belgium, germany ) )
{
Failure( luxembourg );
}
if ( !italy.AddToNeighborsColors( france, austria, switzerland ) )
{
Failure( italy );
}
if ( !switzerland.AddToNeighborsColors( france, italy, austria, germany ) )
{
Failure( switzerland );
}
if ( !austria.AddToNeighborsColors( italy, switzerland, germany ) )
{
Failure( austria );
}
}
static void Failure( Country country )
{
Console.WriteLine( "Failure: a color could not be re-assigned to {0}", country.Name );
}
The final step is to display the name and color of each country along with the name and color of its neighbors enclosed in square brackets.
static void ShowCountriesAndNeighbors()
{
Console.WriteLine( "\nReport colors:\n" );
foreach ( CountryEnum country in Enum.GetValues( typeof( CountryEnum ) ) )
{
int iCountry = (int)country;
Console.Write( Countries[ iCountry ].ToString() );
Console.WriteLine( Countries[ iCountry ].NeighborsColorsToString() );
}
}
Sample Executions of function ColorWesterEurope
Since function ColorWesternEurope does not rely on backtracking or continuations, most of the time it fails to color the map. However, in some runs, it does succeed in solving the four-color problem. The following sample outputs show two successful colorings (files _out 020 success.txt and _out 028 success.txt in the attached ZIP file) and a failed one (file _out 027 failures.txt). The outputs have been edited only to remove extra blank lines.
_out 020 success.txt
ColorWesternEurope:
Initial colors:
Portugal: white
Spain: blue
France: red
Belgium: blue
Holland: red
Germany: blue
Luxembourg: blue
Italy: blue
Switzerland: blue
Austria: blue
FillNeighborsColors:
Report colors:
Portugal: white
[Spain: yellow]
Spain: yellow
[France: red] [Portugal: white]
France: red
[Spain: yellow] [Italy: yellow] [Switzerland: white]
[Belgium: white] [Germany: yellow] [Luxembourg: blue]
Belgium: white
[France: red] [Holland: red] [Luxembourg: blue]
[Germany: yellow]
Holland: red
[Belgium: white] [Germany: yellow]
Germany: yellow
[France: red] [Austria: red] [Switzerland: white]
[Holland: red] [Belgium: white] [Luxembourg: blue]
Luxembourg: blue
[France: red] [Belgium: white] [Germany: yellow]
Italy: yellow
[France: red] [Austria: red] [Switzerland: white]
Switzerland: white
[France: red] [Italy: yellow] [Austria: red]
[Germany: yellow]
Austria: red
[Italy: yellow] [Switzerland: white] [Germany: yellow]
Press any key to continue . . .
_out 028 success.txt
ColorWesternEurope:
Initial colors:
Portugal: red
Spain: blue
France: red
Belgium: yellow
Holland: red
Germany: white
Luxembourg: white
Italy: blue
Switzerland: white
Austria: red
FillNeighborsColors:
Report colors:
Portugal: yellow
[Spain: blue]
Spain: blue
[France: red] [Portugal: yellow]
France: red
[Spain: blue] [Italy: blue] [Switzerland: yellow]
[Belgium: yellow] [Germany: blue] [Luxembourg: white]
Belgium: yellow
[France: red] [Holland: red] [Luxembourg: white]
[Germany: blue]
Holland: red
[Belgium: yellow] [Germany: blue]
Germany: blue
[France: red] [Austria: red] [Switzerland: yellow]
[Holland: red] [Belgium: yellow] [Luxembourg: white]
Luxembourg: white
[France: red] [Belgium: yellow] [Germany: blue]
Italy: blue
[France: red] [Austria: red] [Switzerland: yellow]
Switzerland: yellow
[France: red] [Italy: blue] [Austria: red]
[Germany: blue]
Austria: red
[Italy: blue] [Switzerland: yellow] [Germany: blue]
Press any key to continue . . .
_out 027 failures.txt
ColorWesternEurope:
Initial colors:
Portugal: red
Spain: red
France: yellow
Belgium: red
Holland: white
Germany: red
Luxembourg: yellow
Italy: white
Switzerland: red
Austria: white
FillNeighborsColors:
Failure: a color could not be re-assigned to Belgium
Failure: a color could not be re-assigned to Holland
Failure: a color could not be re-assigned to Germany
Report colors:
Portugal: blue
[Spain: white]
Spain: white
[France: blue] [Portugal: blue]
France: blue
[Spain: white] [Italy: yellow] [Switzerland: red]
[Belgium: white] [Germany: blue] [Luxembourg: yellow]
Belgium: white
[France: blue] [Holland: white] [Luxembourg: yellow]
[Germany: blue]
Holland: white
[Belgium: white] [Germany: blue]
Germany: blue
[France: blue] [Austria: white] [Switzerland: red]
[Holland: white] [Belgium: white] [Luxembourg: yellow]
Luxembourg: yellow
[France: blue] [Belgium: white] [Germany: blue]
Italy: yellow
[France: blue] [Austria: white] [Switzerland: red]
Switzerland: red
[France: blue] [Italy: yellow] [Austria: white]
[Germany: blue]
Austria: white
[Italy: yellow] [Switzerland: red] [Germany: blue]
Press any key to continue . . .
Conclusion
This article has presented the implementation of various versions of John McCarthy’s ambiguity (amb) operator, and its use in the implementation of a non-deterministic function to tackle the four-color problem on the countries of western Europe. As can be seen, the code is indeed non-deterministic because the successful colorings are different.
Using the Code
All the code described in this article is in the attached ZIP file. There are three C# files: Program.cs, Country.cs and Fn.cs, along with five sample outputs in text files. Create a Visual Studio console application named AmbiguousFunctions. Replace the Program class with the one from the Program.cs file. Right-click on the project name and add a new item, a class named Country. Replace the class definition with the code in file Country.cs. Do the same for another new item, a class named Fn and replace the class definition with the code in file Fn.cs. Build the solution and start it without debugging.
History
- 3rd February, 2021: Initial version
