This is the third article in the Build the Forest series of articles. It will build one variant of the Binary Search Tree – Threaded Binary Search Tree.
Introduction
The article is the third one of the Build the Forest in Python Series. In the previous article, Binary Tree Traversal, we talked about the binary tree traversals using recursive approach and auxiliary stack. This article will build one variant of the Binary Search Tree – Threaded Binary Search Tree. Threaded binary search trees utilize empty left or right nodes' attributes to achieve certain traversals without using a stack or recursive approach.
Project Setup
Like other articles in the Build the Binary Search Tree, the implementation assumes Python 3.9 or newer. This article adds two modules to our project: single_threaded_binary_trees.py for the threaded binary search tree implementation and test_single_threaded_binary_trees.py for its unit tests. After adding these two files, our project layout becomes the following:
forest-python
├── forest
│ ├── __init__.py
│ ├── binary_trees
│ │ ├── __init__.py
│ │ ├── binary_search_tree.py
│ │ ├── single_threaded_binary_trees.py
│ │ └── traversal.py
│ └── tree_exceptions.py
└── tests
├── __init__.py
├── conftest.py
├── test_binary_search_tree.py
├── test_single_threaded_binary_trees.py
└── test_traversal.py
(The complete code is available at forest-python.)
What is Threaded Binary Trees?
A threaded binary tree is a binary tree variant that optimizes traversal in a particular order by utilizing the empty left or right attributes of nodes. There are two types of threaded binary trees:
- Single-threaded binary tree: For any empty left or right attribute of a node, the empty attribute is threaded towards either the in-order predecessor or successor. In other words, instead of letting the left or right attribute be empty, the left or right attribute points to the node's predecessor or successor. There are two ways to implement a single-threaded binary tree: left single-threaded binary tree and right single-threaded binary tree.
- Right single-threaded binary tree: The empty right attribute of a node points to the node's successor, and if a node has an empty left attribute, the attribute remains empty.
- Left single-threaded binary tree: The empty left attribute of a node points to the node's predecessor, and if a node has an empty right attribute, the attribute remains empty.
- Double-threaded binary tree: For any empty left or right attribute, the empty attributes are threaded towards either the in-order predecessor or successor: If the left attribute is empty, the left attribute points to the node's predecessor; if the right attribute is empty, the right attribute points to the node's successor.
Although threads can be added to any binary tree, it is most beneficial to add threads to a binary search tree or its variants, i.e., a tree that satisfies the binary-search-tree-property. Therefore, in this project, the threaded binary trees we will implement are binary search trees with threads (threaded binary search trees). In the rest of the article, all the threaded binary trees we refer to are also binary search trees to avoid the wordy phase.
Besides, a thread does not need to point to its in-order predecessor or successor. It can be pre-order or post-order as well. However, in-order is a sorted order in a binary search tree, so a thread that points to its in-order predecessor or successor is most common.
Why Do We Need Threads?
Adding threads to a binary tree increase complexity, so why do we need threads? There are few reasons:
- Fast successor or predecessor access
- No auxiliary stack or recursion approach for certain traversals
- Reduced the memory consumption when performing traversals since no auxiliary stack or recursion are required
- Utilize wasted space. Since the empty left or right attribute of a node does not store anything, we can use them as threads
For each type of threaded binary tree, we can summarize the benefits of adding threads like below:
- The right threaded binary tree can perform in-order and pre-order traversals without a stack or recursive approach. It also has fast successor access.
- The left threaded binary tree can perform reverse in-order traversals without a stack or recursive approach and has fast predecessor access.
- The double-threaded binary tree has the advantages of both types of single-threaded binary trees.
Build Single-Threaded Binary Search Trees
As we did in the Build the Binary Search Tree section, this section will walk through the implementation and discuss some thoughts behind the implementation choices.
Node
The node structure is similar to the binary search tree node, except it has an additional field, is_thread. The purpose of the is_thread attribute is to know if a left or right attribute is a thread.
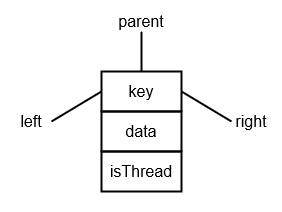
The is_thread attribute is a boolean variable: True if the attribute (left or right depends on the types of single-threaded binary tree) is a thread; False otherwise.
@dataclasses.dataclass
class Node:
key: Any
data: Any
left: Optional["Node"] = None
right: Optional["Node"] = None
parent: Optional["Node"] = None
is_thread: bool = False
As the binary search tree node, we define the node class for threaded binary trees as a dataclass.
Right Single-Threaded Binary Search Tree
As the name implies, we can visualize the right single-threaded binary tree as the picture below:

Each node's empty right attribute points to its in-order successor, and its is_thread variable sets to True except the rightmost node. The rightmost node's right attribute remains empty, and its is_thread is False, so we know it is the rightmost node (i.e., no more successor).
Like the binary search tree, the right threaded binary tree has core functions (insert, delete and search) to build and modify and other auxiliary functions that do not tie to a specific tree, such as getting the leftmost node and get the height of the tree. The same __repr__() function we implemented in the binary search tree can also be used for debugging purposes.
The main difference here is that we implement in-order and pre-order traversals that do not use a stack or use a recursive approach.
class RightThreadedBinaryTree:
def __init__(self) -> None:
self.root: Optional[Node] = None
def __repr__(self) -> str
if self.root:
return (
f"{type(self)}, root={self.root}, "
f"tree_height={str(self.get_height(self.root))}"
)
return "empty tree"
def search(self, key: Any) -> Optional[Node]:
…
def insert(self, key: Any, data: Any) -> None:
…
def delete(self, key: Any) -> None:
…
@staticmethod
def get_leftmost(node: Node) -> Node:
…
@staticmethod
def get_rightmost(node: Node) -> Node:
…
@staticmethod
def get_successor(node: Node) -> Optional[Node]:
…
@staticmethod
def get_predecessor(node: Node) -> Optional[Node]:
…
@staticmethod
def get_height(node: Optional[Node]) -> int:
…
def inorder_traverse(self) -> traversal.Pairs:
…
def preorder_traverse(self) -> traversal.Pairs:
…
Insert
The insert operation is similar to the binary search tree's insertion. The difference is that the threaded binary tree needs to consider the thread update. Therefore, the insertion steps become the following:
- Find the proper location (i.e., the new node's parent) to insert the new node by walking through the tree from the root and comparing the new node's key with each node's key along the way. When walking to the right subtree, check the
is_thread variable as well. If the variable is True, we reach the leaf level, and the leaf node is the parent node of the new node. - Update the new node's parent attribute to point to the parent node.
- If the new node is the parent's left child, set the new node's right attribute to the parent, and set the
is_thread variable to True. Update the parent's left attribute to point to the new node. - If the new node is the right child of its parent, copy the parent's right attribute to the new node's right attribute (the parent's right attribute must be the thread before the insertion), and set the
is_thread variable to True. Update the parent node's right attribute to point to the new node and set the parent's is_thread to False.
The picture below demonstrates the steps of node insertion.

We can implement the insertion as the following:
def insert(self, key: Any, data: Any) -> None:
new_node = Node(key=key, data=data)
parent: Optional[Node] = None
current: Optional[Node] = self.root
while current:
parent = current
if new_node.key < current.key:
current = current.left
elif new_node.key > current.key:
if current.is_thread:
current = None
else:
current = current.right
else:
raise tree_exceptions.DuplicateKeyError(key=new_node.key)
new_node.parent = parent
if parent is None:
self.root = new_node
elif new_node.key < parent.key:
parent.left = new_node
new_node.right = parent
new_node.is_thread = True
else:
new_node.is_thread = parent.is_thread
new_node.right = parent.right
parent.is_thread = False
parent.right = new_node
Search
The search operation is also similar to the search of a binary search tree, but it needs to check the is_thread variable to determine if we reach the leaf level or not.
- Walkthrough the tree from the root and compare the key with each node's key along the tree walk
- If a key matches, we found the node.
- If no key matches after reaching the leaf (if
is_thread is True, it means the node is a leaf node), it does not exist in the tree.
The implement is similar to the binary search tree we made in the binary search tree with a simple modification – check is_thread.
def search(self, key: Any) -> Optional[Node]:
current = self.root
while current:
if key == current.key:
return current
elif key < current.key:
current = current.left
else:
if current.is_thread:
break
current = current.right
return None
Delete
Like the binary search tree, the right threaded tree node to be deleted has three cases: no child, only one child, two children. We also use the transplant technique that we did in the Binary Search Tree: Delete to replace a subtree with the node to be deleted. Although the basic idea is the same, both the transplant function and the delete function need to take the right thread into a count. The most important thing we need to keep in mind is that when we delete a node if there is another node's right attribute that points to the node to be deleted, we need to update the node's thread (i.e., right attribute).
Case 1: No Child
If the node to be deleted has no child, its left attribute is empty, and its is_thread is True. Regarding the threads, there are two cases we need to consider. See the picture below:

Case 2a: Only One Left Child
If the node to be deleted has only one left child, it means the node's is_thread is True (The exception is when the node to be deleted is the root and has only one left child; in this case, the node’s is_thread is False and its right attribute is None). The situations that we need to update the threads are like the picture below:

Case 2b: Only One Right Child
If the node to be deleted has only one right child, it means the node's left attribute is empty, and is_thread is False. Since the node to be deleted has no left child, it means no one points to the node.

Case 3: Two Children
Similar to the binary search tree delete, the case of the node to be deleted has two children can be broken down into two subcases:
3.a The right child of the deleting node is also the leftmost node in the right subtree.
In this case, the right child must have only one right child. Therefore, we can replace the deleting node with its right child, as shown in the picture below:

3.b. The right child of the deleting node also has two children.
In this case, we find the leftmost node from the right subtree to replace the node to be deleted. Note that when we take out the leftmost node from the right subtree, it also falls into the deletion cases: case 1: no child or case 2: only one right child. Otherwise, it cannot be the leftmost node.
Therefore, we use the transplant function twice: one to take out the leftmost node and the other one to replace the deleting node with the original leftmost node. The picture below demonstrates the thread consideration when we perform deleting.
The replacing node has no child:

The replacing node has only one right child:

Based on the pictures above, we can implement the delete and transplant functions as the following:
def delete(self, key: Any) -> None:
if self.root and (deleting_node := self.search(key=key)):
if deleting_node.left is None and (
deleting_node.right is None or deleting_node.is_thread
):
self._transplant(deleting_node=deleting_node, replacing_node=None)
elif deleting_node.left and (
deleting_node.is_thread or deleting_node.right is None
):
predecessor = self.get_predecessor(node=deleting_node)
if predecessor:
predecessor.right = deleting_node.right
self._transplant(
deleting_node=deleting_node, replacing_node=deleting_node.left
)
elif deleting_node.left is None and deleting_node.is_thread is False:
self._transplant(
deleting_node=deleting_node, replacing_node=deleting_node.right
)
elif (
deleting_node.left
and deleting_node.right
and deleting_node.is_thread is False
):
predecessor = self.get_predecessor(node=deleting_node)
replacing_node: Node = self.get_leftmost(node=deleting_node.right)
if replacing_node.parent != deleting_node:
if replacing_node.is_thread:
self._transplant(
deleting_node=replacing_node, replacing_node=None
)
else:
self._transplant(
deleting_node=replacing_node,
replacing_node=replacing_node.right,
)
replacing_node.right = deleting_node.right
replacing_node.right.parent = replacing_node
replacing_node.is_thread = False
self._transplant(
deleting_node=deleting_node, replacing_node=replacing_node
)
replacing_node.left = deleting_node.left
replacing_node.left.parent = replacing_node
if predecessor and predecessor.is_thread:
predecessor.right = replacing_node
else:
raise RuntimeError("Invalid case. Should never happened")
def _transplant(self, deleting_node: Node, replacing_node: Optional[Node]) -> None:
if deleting_node.parent is None:
self.root = replacing_node
if self.root:
self.root.is_thread = False
elif deleting_node == deleting_node.parent.left:
deleting_node.parent.left = replacing_node
if replacing_node:
if deleting_node.is_thread:
if replacing_node.is_thread:
replacing_node.right = replacing_node.right
else:
deleting_node.parent.right = replacing_node
if replacing_node:
if deleting_node.is_thread:
if replacing_node.is_thread:
replacing_node.right = replacing_node.right
else:
deleting_node.parent.right = deleting_node.right
deleting_node.parent.is_thread = True
if replacing_node:
replacing_node.parent = deleting_node.parent
Get the Height
To calculate the tree height of a threaded binary tree, we can recursively increment the height by one for each child's height as we did in the binary search tree. If a node has two children, we use the max function to get the bigger height from the children and increase the highest by one. The main difference is that we use is_thread to check if a node has a right child or not.
@staticmethod
def get_height(node: Optional[Node]) -> int:
if node:
if node.left and node.is_thread is False:
return (
max(
RightThreadedBinaryTree.get_height(node.left),
RightThreadedBinaryTree.get_height(node.right),
)
+ 1
)
if node.left:
return RightThreadedBinaryTree.get_height(node=node.left) + 1
if node.is_thread is False:
return RightThreadedBinaryTree.get_height(node=node.right) + 1
return 0
Get the Leftmost and Rightmost Nodes
The implementation of getting the leftmost and rightmost nodes is similar to the binary search tree. To get the rightmost node, in addition to check if the right attribute is empty, we also need to check if is_thread is True. So, we can modify the get_rightmost function like the following:
@staticmethod
def get_rightmost(node: Node) -> Node:
current_node = node
while current_node.is_thread is False and current_node.right:
current_node = current_node.right
return current_node
The get_leftmost implementation is identical to the get_leftmost in the binary search tree.
@staticmethod
def get_leftmost(node: Node) -> Node:
current_node = node
while current_node.left:
current_node = current_node.left
return current_node
Predecessor and Successor
Since the right threaded tree offers fast in-order successor access (if a node's right attribute is a thread, the right attribute points to the node's in-order successor), we can get the node's successor by following its right attribute if the right attribute is a thread. Otherwise, the node's successor is the leftmost node of the node's right subtree.
@staticmethod
def get_successor(node: Node) -> Optional[Node]:
if node.is_thread:
return node.right
else:
if node.right:
return RightThreadedBinaryTree.get_leftmost(node=node.right)
return None
The implementation of get_predecessor is identical to the binary search predecessor function.
@staticmethod
def get_predecessor(node: Node) -> Optional[Node]:
if node.left:
return RightThreadedBinaryTree.get_rightmost(node=node.left)
parent = node.parent
while parent and node == parent.left:
node = parent
parent = parent.parent
return parent
In-Order Traversal
One benefit the right threaded tree provides is that we can do in-order traversal without using an auxiliary or recursive approach. The algorithm is the following:
- Start from the leftmost node of the entire tree.
- If the right attribute is a thread, follow the right attribute; if the right attribute is not a thread, go to the subtree's leftmost node.
- Repeat step 2 until the right attribute is
None.
The red arrows from the picture below demonstrate the in-order traversal with threads.

And implement the function without using auxiliary stack or recursive.
def inorder_traverse(self) -> traversal.Pairs:
if self.root:
current: Optional[Node] = self.get_leftmost(node=self.root)
while current:
yield (current.key, current.data)
if current.is_thread:
current = current.right
else:
if current.right is None:
break
current = self.get_leftmost(current.right)
Pre-Order Traversal
The right threaded tree also provides an easier way to do pre-order traversal, and it is simpler than in-order traversal.
- Start from the root.
- If the left attribute is not empty, go to the left child.
- If the left attribute is empty, follow the thread to the right.
- Repeat steps 2 and 3 until the right attribute is empty.
The following red arrows in the picture below show the threaded way in-order traversal.

The pre-order traversal can be implemented as the following:
def preorder_traverse(self) -> traversal.Pairs:
current = self.root
while current:
yield (current.key, current.data)
if current.is_thread:
current = current.right.right
else:
current = current.left
Left Single-Threaded Binary Search Tree
The left threaded tree is symmetric to the right threaded tree. If any node's left attribute is empty in the left threaded tree, the left attribute is a thread and points to the node's in-order predecessor, and the is_thread variable sets to True. A left threaded tree can be visualized in the picture below.

The class layout of the left threaded tree is almost the same as the right threaded tree. The only difference is that the left threaded tree offers a simple reversed in-order traversal instead of in-order and pre-order traversals.
class LeftThreadedBinaryTree:
def __init__(self) -> None:
self.root: Optional[Node] = None
def __repr__(self) -> str
if self.root:
return (
f"{type(self)}, root={self.root}, "
f"tree_height={str(self.get_height(self.root))}"
)
return "empty tree"
def search(self, key: Any) -> Optional[Node]:
…
def insert(self, key: Any, data: Any) -> None:
…
def delete(self, key: Any) -> None:
…
@staticmethod
def get_leftmost(node: Node) -> Node:
…
@staticmethod
def get_rightmost(node: Node) -> Node:
…
@staticmethod
def get_successor(node: Node) -> Optional[Node]:
…
@staticmethod
def get_predecessor(node: Node) -> Optional[Node]:
…
@staticmethod
def get_height(node: Optional[Node]) -> int:
…
def reverse_inorder_traverse(self) -> traversal.Pairs:
…
Insert
The insert operation is similar to the right-threaded tree. The difference is the thread is on the left side.
- Find the proper location (i.e., the new node's parent) to insert the new node by walking through the tree from the root and comparing the new node's key with each node's key along the way. When walking to the left subtree, check the
is_thread variable as well. If the variable is True, we reach the leaf level, and the leaf node is the parent node. - After finding the parent node, update the parent's left (or right depends on the key) to point to the new node.
- Update the new node's parent attribute to point to the parent node.
- If the new node is the right child of its parent, point the new node's left attribute to the parent, and set the
is_thread variable to True. - If the new node is the parent's left child, copy the parent's left attribute to the new node's left attribute (the parent's left attribute must be a thread before the insertion) and set
is_thread True. Update the parent node's left attribute to point to the new node.
The picture below demonstrates the steps of the node insertion.

The implementation is the following:
def insert(self, key: Any, data: Any) -> None:
new_node = Node(key=key, data=data)
parent: Optional[Node] = None
current: Optional[Node] = self.root
while current:
parent = current
if new_node.key < current.key:
if current.is_thread:
current = None
else:
current = current.left
elif new_node.key > current.key:
current = current.right
else:
raise tree_exceptions.DuplicateKeyError(key=new_node.key)
new_node.parent = parent
if parent is None:
self.root = new_node
elif new_node.key > parent.key:
parent.right = new_node
new_node.left = parent
new_node.is_thread = True
else:
new_node.is_thread = parent.is_thread
new_node.left = parent.left
parent.is_thread = False
parent.left = new_node
Search
The search operation is similar to the right-threaded binary tree, so we need to check the is_thread variable to determine if we reach the leaf.
- Walkthrough the tree from the root and compare the key with each node's key along the tree walk
- If a key matches, we found the node.
- If no key matches after reaching the leaf (if
is_thread is True, it also means the node is a leaf node), it does not exist in the tree.
The implementation is very similar to the search in the right threaded tree.
def search(self, key: Any) -> Optional[Node]:
current = self.root
while current:
if key == current.key:
return current
elif key < current.key:
if current.is_thread is False:
current = current.left
else:
break
else:
current = current.right
return None
Delete
Similarly, the left threaded binary tree's deletion is symmetric to the right threaded binary tree and has three cases: no child, only one child, two children.
Case 1: No Child

Case 2a: Only One Left Child

Case 2b: Only One Right Child

Case 3: Two Children
3.a The right child of the deleting node is also the leftmost node in the right subtree.

3.b. The right child of the deleting node also has two children.
The replacing node has no child:

The replacing node has only one right child:

Like the right threaded binary tree, we also use the transplant technique that we did in the binary search tree delete to replace a subtree with the node to be deleted.
def delete(self, key: Any) -> None:
if self.root and (deleting_node := self.search(key=key)):
if deleting_node.right is None and (
deleting_node.left is None or deleting_node.is_thread
):
self._transplant(deleting_node=deleting_node, replacing_node=None)
elif (deleting_node.right is None) and (deleting_node.is_thread is False):
self._transplant(
deleting_node=deleting_node, replacing_node=deleting_node.left
)
elif deleting_node.right and (
deleting_node.is_thread or deleting_node.left is None
):
successor = self.get_successor(node=deleting_node)
if successor:
successor.left = deleting_node.left
self._transplant(
deleting_node=deleting_node, replacing_node=deleting_node.right
)
elif deleting_node.right and deleting_node.left:
replacing_node: Node = self.get_leftmost(node=deleting_node.right)
successor = self.get_successor(node=replacing_node)
if replacing_node.parent != deleting_node:
self._transplant(
deleting_node=replacing_node,
replacing_node=replacing_node.right,
)
replacing_node.right = deleting_node.right
replacing_node.right.parent = replacing_node
self._transplant(
deleting_node=deleting_node, replacing_node=replacing_node
)
replacing_node.left = deleting_node.left
replacing_node.left.parent = replacing_node
replacing_node.is_thread = False
if successor and successor.is_thread:
successor.left = replacing_node
else:
raise RuntimeError("Invalid case. Should never happened")
def _transplant(self, deleting_node: Node, replacing_node: Optional[Node]) -> None:
if deleting_node.parent is None:
self.root = replacing_node
if self.root:
self.root.is_thread = False
elif deleting_node == deleting_node.parent.left:
deleting_node.parent.left = replacing_node
if replacing_node:
if deleting_node.is_thread:
if replacing_node.is_thread:
replacing_node.left = deleting_node.left
else:
deleting_node.parent.left = deleting_node.left
deleting_node.parent.is_thread = True
else:
deleting_node.parent.right = replacing_node
if replacing_node:
if deleting_node.is_thread:
if replacing_node.is_thread:
replacing_node.left = deleting_node.left
if replacing_node:
replacing_node.parent = deleting_node.parent
Get the Height
The get_height function is symmetric to the right threaded binary tree.
@staticmethod
def get_height(node: Optional[Node]) -> int:
if node:
if node.right and node.is_thread is False:
return (
max(
LeftThreadedBinaryTree.get_height(node.left),
LeftThreadedBinaryTree.get_height(node.right),
)
+ 1
)
if node.right:
return LeftThreadedBinaryTree.get_height(node=node.right) + 1
if node.is_thread is False:
return LeftThreadedBinaryTree.get_height(node=node.left) + 1
return 0
Get the Leftmost and Rightmost Nodes
Since the left threaded tree is symmetric to the right threaded tree, we need to check if is_thread is True and check if the left attribute is empty when we try to get the leftmost node.
@staticmethod
def get_leftmost(node: Node) -> Node:
current_node = node
while current_node.left and current_node.is_thread is False:
current_node = current_node.left
return current_node
The get_rightmost implementation is identical to the get_rightmost in the binary search tree.
@staticmethod
def get_rightmost(node: Node) -> Node:
current_node = node
while current_node.right:
current_node = current_node.right
return current_node
Predecessor and Successor
By the definition of the left threaded tree: a node's empty left attribute points its in-order predecessor. We can simply get a node's predecessor by following the thread if the node's is_thread is True.
@staticmethod
def get_predecessor(node: Node) -> Optional[Node]:
if node.is_thread:
return node.left
else:
if node.left:
return LeftThreadedBinaryTree.get_rightmost(node=node.left)
return None
The implementation of get_successor is identical to the binary search tree successor.
@staticmethod
def get_successor(node: Node) -> Optional[Node]:
if node.right:
return LeftThreadedBinaryTree.get_leftmost(node=node.right)
parent = node.parent
while parent and node == parent.right:
node = parent
parent = parent.parent
return parent
Reverse In-Order Traversal
With the left threads, neither recursive nor auxiliary stack is required for the left threaded tree to perform reversed in-order traversal.
- Start from the rightmost node of the entire tree.
- If the left attribute is a thread, follow the thread; if the left attribute is not a thread, go to the subtree's rightmost node.
- Repeat step 2 until the left attribute is
None.
The red arrows from the picture below demonstrate the threaded way of reversed in-order traversal.

The following is the implementation:
def reverse_inorder_traverse(self) -> traversal.Pairs:
if self.root:
current: Optional[Node] = self.get_rightmost(node=self.root)
while current:
yield (current.key, current.data)
if current.is_thread:
current = current.left
else:
if current.left is None:
break
current = self.get_rightmost(current.left)
Test
As always, we should have unit tests for our code as much as possible. Here, we use the basic_tree function in conftest.py that we created in Build the Binary Search Tree to test our single-threaded binary trees. Check test_single_threaded_binary_trees.py for the complete unit test.
Analysis
The run time of threaded binary trees' operations is the same as the normal binary search tree.

Although the right threaded tree offers an easier way to retrieve a node's successor and the left threaded tree provides a more straightforward way to get a node's predecessor, the threads do not save a lot of run time. The main reason is that these functions still need to call get_leftmost and get_rightmost functions, which have O(lg n) average run time and O(n) run time on the worst case.
However, the threads do help the space complexity on specific traversals.

Example
Adding threads to the binary search tree makes its implementation more complicated, but they could be a solution when traversals are critical, but space consumption is concerned. For example, we want to build a database that users will access the data in ascending and descending orders a lot, but we have limited memory (i.e., unable to use an auxiliary stack or recursive approach because space consumption is concerned). In this case, we can use threaded binary trees to implement the indexes for ascending and descending accesses.
from typing import Any
from forest.binary_trees import single_threaded_binary_trees
from forest.binary_trees import traversal
class MyDatabase
def __init__(self) -> None:
self._left_bst = single_threaded_binary_trees.LeftThreadedBinaryTree()
self._right_bst = single_threaded_binary_trees.RightThreadedBinaryTree()
def _persist(self, payload: Any) -> str
return f"path_to_{payload}"
def insert_data(self, key: Any, payload: Any) -> None
path = self._persist(payload=payload)
self._left_bst.insert(key=key, data=path)
self._right_bst.insert(key=key, data=path)
def dump(self, ascending: bool = True) -> traversal.Pairs
if ascending:
return self._right_bst.inorder_traverse()
else:
return self._left_bst.reverse_inorder_traverse()
if __name__ == "__main__":
my_database = MyDatabase()
my_database.insert_data("Adam", "adam_data")
my_database.insert_data("Bob", "bob_data")
my_database.insert_data("Peter", "peter_data")
my_database.insert_data("David", "david_data")
print("Ascending...")
for contact in my_database.dump():
print(contact)
print("\nDescending...")
for contact in my_database.dump(ascending=False):
print(contact)
(The complete example is available at single_tbst_database.py.)
The output will look like below:
Ascending...
('Adam', 'path_to_adam_data')
('Bob', 'path_to_bob_data')
('David', 'path_to_david_data')
('Peter', 'path_to_peter_data')
Descending...
('Peter', 'path_to_peter_data')
('David', 'path_to_david_data')
('Bob', 'path_to_bob_data')
('Adam', 'path_to_adam_data')
Summary
Although adding threads increases complexity and does not improve run-time performance, threaded binary trees utilize the wasted left or right attributes and offer a simple way to retrieve predecessor or successor and provide a solution to perform certain traversal without using a stack or recursive approach. When space complexity is concerned, and the specific traversals (e.g., in-order traversal) are critical, threaded binary trees could be a solution.
The following article will build the double-threaded binary tree with both single-threaded binary trees' benefits and is also more complicated.
History
- 3rd April, 2021: Initial version
