This article describes a C# library that implements Stern-Brocot trees for the rational approximation of floating-point numbers.
Introduction
Stern-Brocot trees are named after Moritz Stern and Achille Brocot who independently discovered them. A Stern-Brocot tree is an infinite, complete binary-search tree whose nodes stand in a one-to-one correspondence with the positive rational numbers, and it is used to find the closest rational approximation to an arbitrary floating-point number. The following figure, taken from Wikipedia, illustrates a partial 4-level Stern-Brocot tree.
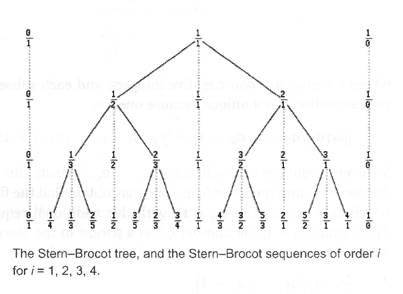
The rationals stored in each node are caculated using the following simple rule. The value stored in the left child of a given parent node equals the value in the parent plus the rational on the vertical line to the left of the child. However, the additions are not performed in ordinary rational arithmetic, but simply by adding the corresponding numerators and denominators. For example, the rationals on the leftmost branch of the tree under the root are: (1+0)/(1+1) = 1/2, (1+0)/(2+1) = 1/3, (1+0)/(3+1) = 1/4. Likewise, the left child of the 2/3 parent node contains the rational (2+1)/(3+2) = 3/5. In the case of right children of parent nodes, they contain the rational of the parent plus the rational on the vertical line to their right. For example, the rationals on the rightmost branch of the tree under the root are: (1+1)/(1+0) = 2/1, (2+1)/(1+0) = 3/1, (3+1)/(1+0) = 4/1. Similarly, the right child of the 3/2 parent node contains the rational (3+2)/(2+1) = 5/3. The results of all these additions are called mediants. In general, given two rational numbers p1/n1 and p2/n2, their mediant is (p1 + p2)/(n1 + n2).
Implementation of Stern-Brocot Trees by a C# Library
The C# code to be described is largely based on the unmanaged C++ code written by Mircea Neacsu in 2016 and published in The Code Project on March 22 of 2021. (See Stern-Brocot Trees and their Applications.) For ease of reference, the names of all the functions in the C++ code have been maintained in the C# library, but there are several additional functions that are original. The library does not implement prime factorizations provided by the C++ code and used on demand. All the code of the library is defined within the namespace SBTlib.
Stern-Brocot Tree Nodes
The fundamental data structure for Stern-Brocot trees is defined by a class to implement its nodes. A node contains two integers _p and _q , corresponding to the numerator and denominator of a rational number, and references to its left and right children plus a reference to its parent. By definition, the parent of the root of the tree is null.
using System;
namespace SBTlib
{
public class SBTnode
{
public int _p, _q;
public SBTnode left, right, parent;
public SBTnode( SBTnode _parent )
{
_p = _q = 0;
left = right = null;
parent = _parent;
}
}
}
Stern-Brocot Trees
The class to implement Stern-Brocot trees will be described in a stepwise fashion. The complete code is in the ZIP file attached to the article. To begin with, the class must provide a constructor.
using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.Windows.Forms;
namespace SBTlib
{
public class SBTree
{
SBTnode root;
public SBTree()
{
Reset();
}
public void Reset()
{
root = new SBTnode( null );
root._p = root._q = 1;
Grow( root );
}
The C++ code does not contain a class for the trees because the nodes are implemented by means of a struct. The SBTree class constructor simply calls function Reset to initialize (or re-initialize) the root of the tree. The parent of the root is set to null, the numerator and denominator of the root are set to 1, and function Grow is called to initialize the root’s children.
private void Grow( SBTnode node )
{
SBTnode left = new SBTnode( node );
node.left = left;
if ( node._p == 1 )
{
left._p = 1;
left._q = node._q + 1;
}
else
{
SBTnode previous = Previous( node );
left._p = node._p + previous._p;
left._q = node._q + previous._q;
}
SBTnode right = new SBTnode( node );
node.right = right;
if ( node._q == 1 )
{
right._q = 1;
right._p = node._p + 1;
}
else
{
SBTnode next = Next( node );
right._p = node._p + next._p;
right._q = node._q + next._q;
}
}
It is important to observe that, being infinite binary-search trees, Stern-Brocot trees are not implemented in full. They grow as needed during the search for a rational approximation to a floating-point number. That is the purpose of function Grow.
The following two functions Previous and Next are used when growing left and right children nodes are mediants of their parent and, respectively, their previous or next node.
private SBTnode Previous( SBTnode node )
{
Debug.Assert( node.parent != null );
while ( node.parent.right != null && node.parent.right != node )
{
node = node.parent;
}
return node.parent;
}
private SBTnode Next( SBTnode node )
{
Debug.Assert( node.parent != null );
while ( node.parent.left != null && node.parent.left != node )
{
node = node.parent;
}
return node.parent;
}
The C++ code computes the rational approximation to a floating-point number in its main function. Since the C# code implements a library, there cannot be a Main function. Therefore, it provides a function to compute the approximation.
public Results Approximate( double x, int n )
{
if ( NotPositive( x ) )
{
MessageBox.Show(
String.Format( "SBTree.Approximate: argument 'x' (== {0}) must be positive.",
x ) );
return new Results( 0, 1, x, 0.0, new List<Tuple<int,int,double>>() );
}
else
{
double epsilon = Math.Pow( (double)10.0, (double)( -n ) );
double approx = (double)1.0;
List<Tuple<int, int, double>> sequence = new List<Tuple<int, int, double>>();
SBTnode current = root;
do
{
sequence.Add( new Tuple<int, int, double>( current._p, current._q, approx ) );
if ( x > approx )
{
current = current.right;
}
else
{
current = current.left;
}
Grow( current );
approx = (double)current._p / (double)current._q;
} while ( Math.Abs( x - approx ) > epsilon );
return new Results( current._p, current._q, x, approx, sequence );
}
}
Function Approximate first checks whether the floating-point number is not positive. If so, it displays an appropriate MessageBox and returns an empty sequence of approximations.
private bool NotPositive( double x )
{
string str = x.ToString();
return str.StartsWith( "-" ) || str.Equals( "0" );
}
}
}
Given that exact comparisons of floating-point numbers (especially comparisons with 0.0) are not reliable, function NotPositive converts the floating-point number to a string and checks whether the number was negative or 0.0.
Function Approximate keeps a record of the succesive approximations using a sequence of triples defined as List<Tuple<int, int, double>>, where the first two elements are the numerator and denominator of a rational number and the third is the corresponding floating-point approximation. When the approximation sequence converges, the function returns an instance of class Results containing information about the final result and the sequence of triples. The C++ code does not have code equivalent to this class.
using System;
using System.Collections.Generic;
namespace SBTlib
{
public class Results
{
int numerator, denominator;
double number, approx, error;
List<Tuple<int,int,double>> sequence;
public Results( int p, int q, double x, double _approx,
List<Tuple<int,int,double>> _sequence )
{
numerator = p;
denominator = q;
number = x;
approx = _approx;
error = x - _approx;
sequence = _sequence;
}
public int Numerator { get { return numerator; } }
public int Denominator { get { return denominator; } }
public void Display( int decPlaces )
{
if ( sequence.Count > 0 )
{
Console.WriteLine( "\nRational approximation to {0}\nwith {1} decimal places:\n",
number, decPlaces );
string formatStr
= "{0,4}/{1,4} == {2,"
+ ( decPlaces + 5 ).ToString() + ":F" + decPlaces.ToString() + "}";
foreach ( Tuple<int, int, double> tuple in sequence )
{
Console.WriteLine( formatStr, tuple.Item1, tuple.Item2, tuple.Item3 );
}
Console.WriteLine( "\nFinal result:\n" );
Console.WriteLine( formatStr, numerator, denominator, approx );
Console.WriteLine();
}
}
}
}
Class Results provides a function Display to display the results on a command-prompt window when used by a console application.
Implementing the Library
The ZIP file contains three files that implement the library: SBTnode.cs, SBTree.cs, and Results.cs. In Visual Studio, create a new Visual C# Class Library with the name SBTlib. In the Solution Explorer, right-click on the default class name chosen by Visual Studio (usually Class1.cs), re-name it as SBTnode.cs and copy the code from file SBTnode.cs. Right-click on the solution name and select Add->New Item. In the menu that appears, select Class, name it SBTree.cs and copy the code from file SBTree.cs. In the Solution Explorer, right-click on References and select Add Reference. Select the .NET tab and add a reference to the library System.Windows.Forms. Right-click on the solution name and select Add->New Item. In the menu that appears, select Class, name it Results.cs and copy the code from file Results.cs. Build the solution and the bin\Debug directory will contain the library file SBTlib.dll.
Testing the Library
The following simple console application, also included in the attached ZIP file as Program.cs, can be used to test the library. The code defines a single SBTree and contains four test cases. The first two tests provide valid floating-point numbers and the last two provide invalid numbers.
using System;
using SBTlib;
namespace TestSBTlib
{
class Program
{
static void Main( string[] args )
{
SBTree tree = new SBTree();
Results results;
results = tree.Approximate( 3.14159265359, 6 );
results.Display( 6 );
tree.Reset();
results = tree.Approximate( 0.56, 6 );
results.Display( 6 );
tree.Reset();
results = tree.Approximate( 0.0, 6 );
results.Display( 6 );
tree.Reset();
results = tree.Approximate( -5.67, 6 );
results.Display( 6 );
}
}
}
Observe the calls to function SBTree.Reset between successive tests.
To use the code, create a console application and name it TestSBTlib. In the Solution Explorer, right-click on References and select Add Reference. Select the Browse tab, navigate to the bin\Debug directory of the library and select the file SBTlib.dll generated in the previous section. Copy the code from file Program.cs. Build the solution and start it without debugging. The first two tests produce the results shown in the following figure:

The last two tests produce the MessageBox windows shown in the following two figures, and no resuts are displayed in the command-prompt window.


Practical Use of the Library
As a second simple example of the use of the library, consider an application dealing with quantum computing (which the author is presently working on). The states of any quantum computational system through time are represented by arrays containing probability amplitudes (or just probabilities). Each array corresponds to a particular instant of time. Any further discussion of quantum computational systems and probability amplitudes is beyond the scope of this article. The important point is that a probability can be specified either as a rational number (explicit numerator and denominator) or as a fraction (a floating-point number between 0.0 and 1.0). To handle those two representations, it is convenient to define a class as follows.
The class has four private data members: an instance of a Stern-Brocot tree (SBTree), two int members for the numerator and the denominator of a rational number, and a double member for the fraction equivalent to the rational number. Thus the class maintains both representations of a probability value.
class Probability
{
private SBTree tree = new SBTree();
private int _numerator,
_denominator;
private double _fraction;
The first constructor handles the first representation. It receives two arguments, the numerator and the denominator, and generates the second representation.
public Probability( int numerator, int denominator = 1 )
{
_numerator = 0;
_denominator = 1;
if ( numerator >= 0 && denominator > 0 )
{
_numerator = numerator;
_denominator = denominator;
}
_fraction = (double)_numerator / (double)_denominator;
}
The second constructor handles the second representation. It receives a fractional probability value, and then uses the SBTree.Approximate function to compute the rational number that approximates the fraction if it is not equal to either of the two trivial values 0.0 or 1.0 (those values are identified by functions from a static utility class). From the approximation, the components of the first representation can be set. Every time the second constructor needs to compute an approximation, it calls function SBTree.Reset to reinitialize its private data member tree.
public Probability( double fraction )
{
_fraction = fraction;
if ( Util.IsZero( fraction ) )
{
_numerator = 0; _denominator = 1;
}
else if ( Util.IsOne( fraction ) )
{
_numerator = 1; _denominator = 1;
}
else
{
tree.Reset();
Results results = tree.Approximate( fraction, 6 );
_numerator = results.Numerator;
_denominator = results.Denominator;
}
}
Finally, the class provides three get properties and two functions to convert the probability to a short string and to a long string.
public int Numerator { get { return _numerator; } }
public int Denominator { get { return _denominator; } }
public double Fraction { get { return _fraction; } }
public override string ToString()
{
return String.Format( "{0,2}/{1}", _numerator, _denominator );
}
public string ToLongString()
{
return String.Format( "{0} (== {1,4:F2})", ToString(), _fraction );
}
}
The results from the second valid test case in the previous section correspond to the approximation of the probability value 0.56 by the second constructor of this class.
Conclusion
This article has dealt with the implementation, testing, and practical use of a C# library implementing Stern-Brocot trees. The library can be used by any managed-code Visual Studio application requiring the arbitrary-precision, rational-number approximation of positive floating-point numbers.
History
- 30th April, 2021: Initial version
