In this article, we look at how the AVL tree introduces some complexity on insertion and deletion operations to keep its balance, like how the AVL tree’s self-balancing ability provides O(lg n) time complexity for basic operations, which is better performance than the regular binary search tree.
Introduction
After the Red-Black Tree discussion, this article will implement another variant of the self-balancing binary search tree: the AVL Tree.
Project Setup
Follow the same style and assumption as other articles in the Build the Forest Series, the implementation assumes Python 3.9 or newer. This article adds two modules to our project: avl_tree.py for the AVL tree implementation and test_avl_tree.py for its unit tests. After adding these two files, our project layout becomes the following:
forest-python
├── forest
│ ├── __init__.py
│ ├── binary_trees
│ │ ├── __init__.py
│ │ ├── avl_tree.py
│ │ ├── binary_search_tree.py
│ │ ├── double_threaded_binary_tree.py
│ │ ├── red_black_tree.py
│ │ ├── single_threaded_binary_trees.py
│ │ └── traversal.py
│ └── tree_exceptions.py
└── tests
├── __init__.py
├── conftest.py
├── test_avl_tree.py
├── test_binary_search_tree.py
├── test_double_threaded_binary_tree.py
├── test_red_black_tree.py
├── test_single_threaded_binary_trees.py
└── test_traversal.py
(The complete code is available at forest-python.)
What is an AVL Tree?
An AVL tree (named after the inventors Adelson-Velsky and Landis) is a self-balancing binary search tree. In addition to the binary-search-tree-property, an AVL tree maintains the AVL-tree-property to keep it balanced:
- For every node in an AVL tree, the heights of its left subtree and its right subtree differ by at most one.
The property is also called balance factor and can be rewritten to the following formula:
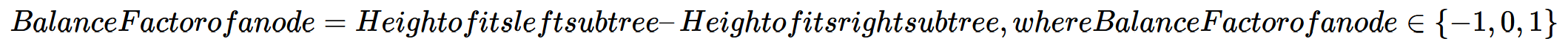
If a node’s balance factor > 0, we call it left-heavy. If a node’s balance factor < 0, we call it right-heavy. If a node’s balance factor = 0, it is called balanced.
(Note that some people define the balance factor as the height of its right subtree – the height of its left subtree. In this case, left-heavy becomes a node’s balance factor < 0, whereas right-heavy happens when a node’s balance factor > 0. However, no matter which definition is used, the concept of the AVL tree is the same.)
A typical AVL tree can be visualized in the picture below:

In the above picture, BF indicates a node’s balance factor. The numbers under the nodes are the height of the nodes. If a node is empty, i.e., None, its height is -1. This way makes it easier to calculate nodes’ balance factor.
Build AVL Tree
This section will walk through the implementation of the AVL tree with some thoughts behind the implementation choices.
Node
Instead of computing a node’s height every time we need it, we store the height in each node. Therefore, the node’s structure has one more field than the binary search tree node.

Storing the height saves the compute time, so we do not need to calculate the height every time we check the balance factor. However, it comes with the cost — we need to keep the height up to date when the AVL tree is modified, such as inserting a node or deleting a node. More details about the height update will come in the insertion and deletion sections.
Like the other binary tree nodes, we utilize the dataclass to define the AVL tree node.
from dataclasses import dataclass
@dataclass
class Node
key: Any
data: Any
left: Optional["Node"] = None
right: Optional["Node"] = None
parent: Optional["Node"] = None
height: int = 0
Class Overview
Like other types of binary trees in the Build the Forest project, the AVL tree class has similar functionalities.
class AVLTree:
def __init__(self) -> None:
self.root: Optional[Node] = None
def __repr__(self) -> str
if self.root:
return (
f"{type(self)}, root={self.root}, "
f"tree_height={str(self.get_height(self.root))}"
)
return "empty tree"
def search(self, key: Any) -> Optional[Node]:
…
def insert(self, key: Any, data: Any) -> None:
…
def delete(self, key: Any) -> None:
…
@staticmethod
def get_leftmost(node: Node) -> Node:
…
@staticmethod
def get_rightmost(node: Node) -> Node:
…
@staticmethod
def get_successor(node: Node) -> Optional[Node]:
…
@staticmethod
def get_predecessor(node: Node) -> Optional[Node]:
…
@staticmethod
def get_height(node: Optional[Node]) -> int:
…
def _get_balance_factor(self, node: Optional[Node]) -> int:
…
def _left_rotate(self, node_x: Node) -> None:
…
def _right_rotate(self, node_x: Node) -> None:
…
def _insert_fixup(self, new_node: Node) -> None:
…
def _transplant(self, deleting_node: Node, replacing_node: Optional[Node]) -> None:
…
def _delete_no_child(self, deleting_node: Node) -> None:
…
def _delete_one_child(self, deleting_node: Node) -> None:
…
def _delete_fixup(self, fixing_node: Node) -> None:
…
We can implement most of the AVL tree functions precisely as the regular binary search tree, such as search and most auxiliary functions. We can also use the traversal functions in Binary Tree Traversal to traverse an AVL tree.
Insert and delete are two operations that may result in an AVL tree imbalance. Therefore, the AVLTree class has methods that help to keep the tree balanced, including _left_rotate(), _right_rotate(), _insert_fixup(), and _delete_fixup(). Since these helper methods mainly keep an AVL tree balanced, we define them as private functions and transparent to the client code.
Rotations
The method to restore the violated AVL-tree-property after insertion or deletion is rotation (similar to the Red-Black Tree: Rotations).
The picture below demonstrates the four cases in that AVL-tree-property could be broken: left-left, left-right, right-left, and right-right.

When we deal with an unbalanced AVL tree, we always start from the bottommost unbalanced node (i.e., the node is either BF > 1 or BF < -1). So, for example, node 23 in the picture above is the bottommost unbalanced node. And then check the balance factor of its child that has the higher height. If the bottommost unbalanced node is left-heavy (i.e., BF > 0) and its child with higher height is left-heavy, it is the left-left case (the leftmost case in the picture above). If the balance factor of the child that has the higher height is right-heavy (i.e., BF < 0), it is the left-right case (the second leftmost case in the picture above). The other cases (right-left and right-right) in the picture are symmetric to the left-left cases and left-right cases.
The following subsections show how rotations rebalance the imbalance cases.
Right Rotation (Left-Left Case)
For the left-left case, we perform the right rotation on the bottommost unbalanced node (node 23 in this case). After the rotation, node 17 becomes the parent of node 23. Also, the height and balance factor of both node 17 and node 23 changed after the rotation.

Left-Right Rotation (Left-Right Case)
If the bottommost unbalanced node is left-heavy, but its child (who has higher height) is right-heavy, we perform left rotation first on the child (node 17 in this case) and then perform right rotation on the bottommost unbalanced node (node 23).

Note that only the nodes that involve the rotation change their balance factor and heights. For example, after the left rotation, node 17 and node 21 change their height and balance factor (highlight in yellow). After the right rotation, only node 21 and node 23 change their height and balance factor (height in green).
Right-Left Rotation (Right-Left Case)
The right-left case is symmetric to the left-right case. Therefore, we perform the right rotation first and the left rotation after.

Left Rotation (Right-Right Case)
The right-right case is symmetric to the left-left case. So we can perform left rotation to make it balance.

Summary
The table below summarizes the unbalanced cases and their solutions.

Insert
Insertion in the AVL tree has one substantial effect: update the height. Therefore, when we insert a node into an AVL tree, the new node may change the tree height, violating the AVL-tree-property. When that happens, we perform the specific rotations to rebalance the tree.
Height Update
Before we implement the insert function, we need to understand how the insertion changes the height. First, note that the new node to be inserted must become a leaf node after the insertion. Therefore, the new node’s height must be 0, and its balance factor is also 0. Besides, if the new node’s parent has a child before the new node’s insertion, the parent and the overall tree’s height remain the same: no height changes, no AVL-tree-property violation.

Second, the height change only happens when the new node’s parent did not have a child before the insertion. In this case, we update the new node’s ancestors’ height all the way to the root (like the picture below), and only the new node’s ancestors have a height update. When the height changes, it means potential AVL-tree-property violations may happen.

(The picture above does not violate the AVL-tree-property. However, we will handle the case that an AVL tree becomes imbalanced after the insertion in the following sections.)
The insert algorithm is modified from the regular binary search tree insert.
- Insert the new node with the height 0 in the same way as the binary search tree insertion: find the proper location (i.e., the parent of the new node) to insert the new node by walking through the tree from the root and comparing the new node’s key with each node’s key along the way.
- Update the height and check if the violated AVL-tree-property happens by traceback from the new node to the root. While traveling back to the root, update each node’s height on the way if necessary. If we find an unbalanced node, perform certain rotation(s) to balance it. After the rotation, the insertion concludes. If no unbalanced node is found, the insertion completes after reaching the root and updating its height.
def insert(self, key: Any, data: Any) -> None:
new_node = Node(key=key, data=data)
parent: Optional[Node] = None
current: Optional[Node] = self.root
while current:
parent = current
if new_node.key < current.key:
current = current.left
elif new_node.key > current.key:
current = current.right
else:
raise tree_exceptions.DuplicateKeyError(key=new_node.key)
new_node.parent = parent
if parent is None:
self.root = new_node
else:
if new_node.key < parent.key:
parent.left = new_node
else:
parent.right = new_node
if not (parent.left and parent.right):
self._insert_fixup(new_node)
Fixup
As the rotations section mentioned, there are four potential unbalanced cases. And we perform specific rotations to restore the AVL-tree-property. After we fix the AVL-tree-property, the AVL tree becomes balanced. No need to keep tracking the ancestors’ balance factor. The following subsections describe the fixup for each case.
Left-Left Case

In the picture above, we add node 19. After the insertion, we start checking the balance factor of node 19’s ancestors from node 17 and up. And then, we find that node 37’s balance factor is unbalanced and left-heavy. We also need to check its child with a higher height to determine which rotation to perform. In the insertion case, the child with a higher height must happen in the path that contains the new node, i.e., node 23 in this case, since node 23’s balance factor is 1 after the insertion. We identify that this is a left-left case.
So we perform the right rotation on node 37. After the right rotation, node 23 becomes the new root, and node 37 becomes node 23’s right child. Note that only the nodes involved in the rotation have height and balance factor change. So, in this case, only node 23 and node 37 have height, and the balance factor changed.
Why There Is No Need to Keep Checking the Ancestors’ Balance Factor After the Rotation?
The height of node 37 was 2, and node 23’s height was 1 before the insertion. After the insertion, node 37’s height became 3, and node 23’s height became 2. Then we performed the rotation. After the rotation, node 23 took node 37’s original position, and node 23’s height became 2, and node 37’s height became 1. Therefore, the height of the same position remains the same, i.e., the root (node 37) had height 2 before the insertion; the root (node 23) still has height 2 after the rotation. In other words, if node 37 has a parent (say x) before the rotation, after the rotation, x‘s left child becomes node 23, but x’s height is not affected. So, we don’t need to keep checking the x’s ancestors’ heights after the rotation.
Left-Right Case

After we identify this is a left-right case by checking the balance factor of the bottommost unbalanced node (node 37) and its child (node 23) with higher height, we perform the left rotation on node 23, so it becomes a left-left case. Then, we perform the right rotation on the unbalanced node (node 37). After that, we restore the violated AVL-tree-property.
Right-Left Case

This case is symmetric to the left-right case, so we perform the right on the unbalanced node’s (node 37) right child (node 43), so it becomes the right-right case. Then, we perform the left rotation on the unbalanced node (node 37). After that, we fix the violated AVL-tree-property.
Right-Right Case

The right-right case is symmetric to the left-left case, so we can restore its AVL-tree property by performing the left rotation.
After the fixup analysis, we can implement the _insert_fixup function like the following. Note that we always update the node’s height while we are walking up the tree and before the rotation.
def _insert_fixup(self, new_node: Node) -> None:
parent = new_node.parent
while parent:
parent.height = 1 + max(
self.get_height(parent.left), self.get_height(parent.right)
)
grandparent = parent.parent
if grandparent:
if self._get_balance_factor(grandparent) > 1:
if self._get_balance_factor(parent) >= 0:
self._right_rotate(grandparent)
elif self._get_balance_factor(parent) < 0:
self._left_rotate(parent)
self._right_rotate(grandparent)
break
elif self._get_balance_factor(grandparent) < -1:
if self._get_balance_factor(parent) <= 0:
self._left_rotate(grandparent)
elif self._get_balance_factor(parent) > 0:
self._right_rotate(parent)
self._left_rotate(grandparent)
break
parent = parent.parent
Search
The search function is identical to the Binary Search Tree: Search.
Delete
The basic idea of the AVL tree deletion is similar to the regular binary search tree. There are three cases of the node to be deleted: no child, only one child, and two children. We also use the same transplant method to replace the subtree rooted at the deleting_node with the subtree rooted at the replacing_node.
Transplant
The transplant method is identical to the Binary Search Tree: Delete.
def _transplant(self, deleting_node: Node, replacing_node: Optional[Node]) -> None:
if deleting_node.parent is None:
self.root = replacing_node
elif deleting_node == deleting_node.parent.left:
deleting_node.parent.left = replacing_node
else:
deleting_node.parent.right = replacing_node
if replacing_node:
replacing_node.parent = deleting_node.parent
Similar to the insertion, the AVL tree deletion may update the tree height and potentially violate the AVL-tree-property, so we need to check if the AVL tree becomes unbalanced and fix it after the deletion.
The overall delete procedure is like a regular binary search tree with some modifications.
- Find the node to be deleted (
deleting_node). - If the
deleting_node has no child, use the transplant method to replace the deleting_node with None. Then, perform the fixup operation. - If the
deleting_node has only one child, use the transplant method to replace the deleting_node with only one child. Then perform the fixup operation. - If the
deleting_node has two children, find the deleting_node‘s successor as the replacing_node. Then, replace the deleting_node‘s key and data with the replacing_node‘s key and data, so the deleting_node is replaced by the replacing_node but keep its original balance factor and height (i.e., no height and balance factor change means no AVL-tree-property violation). After that, delete the replacing_node, which is the same as either step 2 (no child) or step 3 (only one child).
To make the implementation clear, we define the _delete_no_child method for the case that the node to be deleted has no child and the _delete_one_child method for the node to be deleted has only one child. If the node is deleted with two children, we can reuse the _delete_no_child and _delete_one_child accordingly. Furthermore, since the node to be deleted has two children using _delete_no_child and _delete_one_child, only these two methods need to call the _delete_fixup function to fix unbalanced nodes. Thus, we can implement the delete, _delete_no_child, and _delete_one_child functions as the following:
def delete(self, key: Any) -> None:
if self.root and (deleting_node := self.search(key=key)):
if (deleting_node.left is None) and (deleting_node.right is None):
self._delete_no_child(deleting_node=deleting_node)
elif deleting_node.left and deleting_node.right:
replacing_node = self.get_leftmost(node=deleting_node.right)
deleting_node.key = replacing_node.key
deleting_node.data = replacing_node.data
if replacing_node.right:
self._delete_one_child(deleting_node=replacing_node)
else:
self._delete_no_child(deleting_node=replacing_node)
else:
self._delete_one_child(deleting_node=deleting_node)
def _delete_no_child(self, deleting_node: Node) -> None:
parent = deleting_node.parent
self._transplant(deleting_node=deleting_node, replacing_node=None)
if parent:
self._delete_fixup(fixing_node=parent)
def _delete_one_child(self, deleting_node: Node) -> None:
parent = deleting_node.parent
replacing_node = (
deleting_node.right if deleting_node.right else deleting_node.left
)
self._transplant(deleting_node=deleting_node, replacing_node=replacing_node)
if parent:
self._delete_fixup(fixing_node=parent)
Fixup
We know the delete operation may change the height and violate the AVL-tree-property. Like the insertion, there are four potential unbalanced cases. And we perform specific rotations to restore the AVL-tree-property. We also start the fixup procedure from the bottommost unbalanced node. The bottommost unbalanced node must be one of the ancestors of the node to be deleted. However, unlike the insertion fixup, the unbalanced balance factor may propagate above the node we perform the rotations on. Therefore, after we restore the bottommost unbalanced node, we need to check its parent. If its parent becomes unbalanced, fix it. Repeat this process until we reach the root, and the root is also balanced.
No Child
Like we mentioned in the rotations section, four cases could violate the AVL-tree-property. The following picture shows these four cases and how to restore their balance factor if the node to be deleted has no child.

One Child
The following two pictures demonstrate the four cases.
The unbalanced node is left-heavy.

The unbalanced node is right-heavy.

Two Children
Like other binary trees’ deletion, we can see the two children case as two sub-cases: the replacing node is the deleting_node‘s direct child, and the replacing_node is the deleting_node’s leftmost node. In either case, we can transfer the two children case to either the no-child case or the one-child case by replacing the deleting_node with the replacing_node but keep the original height and balance factor. By doing that, we do not change the height and balance factor. After that, we delete the replacing_node, and it becomes either the no-child case or the one-child case. The following pictures show how does the two children deletion works and how to fix its unbalance.
The replacing_node is the deleting_node’s direct child.

The replacing_node is the deleting_node’s leftmost node.

The implementation of the complete fixup operation is the following. Similar to the insertion, we update the node’s height while walking up the tree.
def _delete_fixup(self, fixing_node: Node) -> None:
while fixing_node:
fixing_node.height = 1 + max(
self.get_height(fixing_node.left), self.get_height(fixing_node.right)
)
if self._get_balance_factor(fixing_node) > 1:
if self._get_balance_factor(fixing_node.left) >= 0:
self._right_rotate(fixing_node)
elif self._get_balance_factor(fixing_node.left) < 0:
self._left_rotate(fixing_node.left)
self._right_rotate(fixing_node)
elif self._get_balance_factor(fixing_node) < -1:
if self._get_balance_factor(fixing_node.right) <= 0:
self._left_rotate(fixing_node)
elif self._get_balance_factor(fixing_node.right) > 0:
self._right_rotate(fixing_node.right)
self._left_rotate(fixing_node)
fixing_node = fixing_node.parent
Auxiliary Functions
The auxiliary functions, such as get the leftmost node and get the successor of a node, are identical to the Binary Search Tree: Auxiliary Functions, and the implementation is available at the Github repository. The only auxiliary function different from the binary search tree is the function to get the height.
Get the Height
Since each node has its height stored, to get the node’s height becomes very straightforward: just return the height.
@staticmethod
def get_height(node: Optional[Node]) -> int:
if node:
return node.height
return -1
Traversal
Although the AVL tree node has one additional field (i.e., height) than the normal binary search tree node, we can still use the exact implementation we did in Binary Tree Traversal to traverse an AVL tree. The only modification we need to make is to add the AVL tree as a supported type.
SupportedNode = Union[None, binary_search_tree.Node, avl_tree.Node]
SupportedTree = Union[binary_search_tree.BinarySearchTree, avl_tree.AVLTree]
"""Alisa for the supported tree types. For type checking."""
(See traversal.py for the complete source code.)
The supported type is for type checking, as we discussed at Binary Tree Traversal: Function Interface.
Test
As always, we should have unit tests for our code as much as possible. Check test_avl_tree.py for the complete unit test.
Analysis
AVL tree is a self-balancing binary search tree, and it has height O(lg n), where n is the number of nodes (This can be proved by leveraging the Fibonacci number. See AVL Tree Wikipedia for more detail). Therefore, the time complexity of an AVL tree can be summarized in the table below:

Example
Like the red-black tree, the AVL tree is widely used in software programs because of its self-balancing ability. For example, this section uses the AVL tree we implement here to implement a key-value Map.
from typing import Any, Optional
from forest.binary_trees import avl_tree
from forest.binary_trees import traversal
class Map
def __init__(self) -> None:
self._avlt = avl_tree.AVLTree()
def __setitem__(self, key: Any, value: Any) -> None
self._avlt.insert(key=key, data=value)
def __getitem__(self, key: Any) -> Optional[Any]
node = self._avlt.search(key=key)
if node:
return node.data
return None
def __delitem__(self, key: Any) -> None
self._avlt.delete(key=key)
def __iter__(self) -> traversal.Pairs
return traversal.inorder_traverse(tree=self._avlt)
@property
def empty(self) -> bool
return self._avlt.empty
if __name__ == "__main__":
contacts = Map()
contacts["Mark"] = "mark@email.com"
contacts["John"] = "john@email.com"
contacts["Luke"] = "luke@email.com"
print(contacts["Mark"])
del contacts["John"]
print(contacts["John"])
for contact in contacts:
print(contact)
(The complete example is available at avlt_map.py.)
Summary
Like the red-black tree, the AVL tree introduces some complexity on insertion and deletion operations to keep its balance, but the AVL tree’s self-balancing ability provides O(lg n) time complexity for basic operations, which is better performance than the regular binary search tree.
(Originally published at Shun's Vineyard on June 6, 2021.)
History
- 7th June, 2021: Initial version
