Sudoku Solver using C# Windows Application

• Download source code - 258 KB

Introduction

Sudoku is an interesting puzzle suitable for all ages and available easily. I always wanted to write a program to solve Sudoku puzzle once I got interested in it. I did a brief check to find out any Sudoku solvers on the internet but they are all based on brute force method mostly. I wanted to write the code in the way I try to solve the problem manually. I have tried two times in the past but have only been partially successful. Then with the third attempt, I managed to complete to a reasonable state. To begin with, this program hence doesn’t do any guessing work. If it cannot solve the puzzle, then I try to use the brute force method to solve using possible values which are obtained.

Background

You need to have some understanding of the basics to solve Sudoku. The solution solves the puzzle mostly when one can solve the code without any guessing. For unsolved puzzle, you can use the log to find out possible values, which can be given as an input to try further. I have attached the full working version of the application (EXE) and the source code for further development.

Using the Code

After porting the solution to a different computer, I had an issue with forms rendering due to DPI issue. Hence, I had to use the below code to solve it. Without these lines, Winform looks blur in different machines.

static class Program
    {
        /// <summary>
        /// The main entry point for the application.
        /// </summary>
        [STAThread]
        static void Main()
        {
            // ***this line is added***
            if (Environment.OSVersion.Version.Major >= 6)
                SetProcessDPIAware();

            Application.EnableVisualStyles();
            Application.SetCompatibleTextRenderingDefault(false);
            Application.Run(new SudokuCSharp.Form1());
        }

        // ***also dllimport of that function***
        [System.Runtime.InteropServices.DllImport("user32.dll")]
        private static extern bool SetProcessDPIAware();
    }

Now to the coding part, my solving pattern is as follows:

To hold the problem statement, I created a structure as this:

private struct mStruct
       {
           public bool isLocked;  //To know whether it can be altered or not.
                                  //If Locked, then it cannot be altered
           public int curValue;   //current value
           public bool isSource;  //To know whether this is the source data or not.
           public string posValue;//to list down possible values it can hold
           public int quarter;    //to know which quarter the array belongs
           public string rem;     //remarks columns
       }

Then I created an array out of this to hold the problem statement. The fields of the mstruct are explained here:

• isLocked: boolean type - to know the value cannot be altered. This can be part of an initial problem or a correct value found after iterations. So there is no option to change once it is fixed.
• curvalue: integer - the current value on the cell
• isSource: boolean type - if true, then it is from the problem statement. If false, then it is the value to be found. To differentiate a cell value is from problem statement or a found value.
• posvalue: string - contains all the possible values a cell can hold in comma separated fashion.
• quarter: integer - I have split the entire 9x9 cells into 9 quarters. This value tells in which quarter the cell falls into.
• rem: this is a string to hold any remarks.

I created a 9x9 array with the above struct and hold the problem statement in it. I call this array as playArray as I am going to play with it to find the answers.

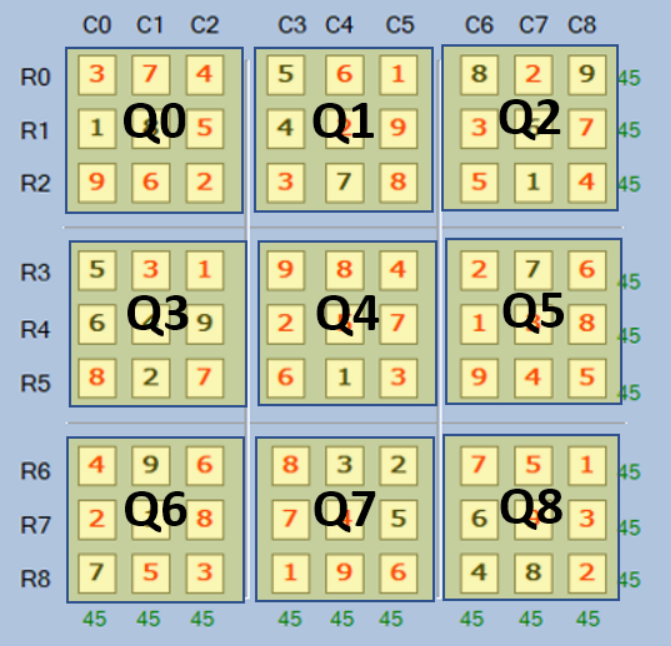
I also did an easy to identify a cell from the textbox control name. All the textbox controls are named as this: 'txtq<quarter>r<row no>c<col no>'. For example, in the text box name 'txtq2r0c7' - txt to define it is a text box, next 2 letters 'q2' tells in which quarter it is - here is second quarter. Next 4 letters 'r0c7' tell the row and col position - 0^th row and 7^th col. In this way, I am able to identify from where the value is coming and also easy to assign the values back to the textbox. Refer to the below image for textbox namings and quarter naming.

The reason for dividing the area into quarters is to solve the 3x3 cells in a quarter. As you know, the simple Sudoku rule: No. 1 - 9 to be there non repetitive in a row and col and quarter.

Loading Problem Statement

It is a bit hard to enter the cells with values from the problem as we need to use the tab to move between the textboxes. Instead, I thought of an easy way to do it - by entering 0 in the cells where there is no value.

For example, the problem statement: 000500809180400060000070010500000070649000000020010000090032000010005600700000480 is loaded as below. The values are entered row wise and all the 0s are assumed as blank on the grid. This helps to load the problem faster.

Solving the Puzzle

The puzzle is tried iteratively till the solution is found. The key function is:

SolveHorizontalVerticalOrQuadrant("q");  //Solve for Quadrant
SolveHorizontalVerticalOrQuadrant("r");  //Solve for Row
SolveHorizontalVerticalOrQuadrant("c");  //Solve for Col

First solve by quarter, then row wise and then column wise. Note the function name is the same except for the parameter 'q','r,'c' to distinguish whether we are solving for quarter, row or col wise. The logic remains the same except based on the parameter that is sent, the array is picked up accordingly and worked upon.

Once I know the list of values in an array, I identify cells that don't have values (cells that need to be solved). Then assign all the possible values to those cells using. To begin with, it can hold all values from 1 to 9. Then I iterate the remaining cells which have values and remove those values from the possible values for that cell.

private readonly string possSolution = @"123456789"; //string that holds all possible values 
                                                     //an empty cell can have

Code where all possible values a cell can hold is determined as below:

//Get possible solution in a line
               for (int j = 0; j < noOfElementsInRowOrCol; j++)
               {
                   if (lStruct[j].curValue > 0)
                   {
                       lPossSolution = lPossSolution.Replace(lStruct[j].curValue.ToString(),
                                       "");//remove the values from possible solution
                   }
                   else
                   {
                       //Get the row and col where the value is 0
                       row = Int32.Parse(lStruct[j].rem.Substring(1, 1));//assuming r1c1
                       col = Int32.Parse(lStruct[j].rem.Substring(3, 1));//
                       zeroCells[k] = row * 10 + col;
                       k += 1;
                   }
               }

There are two ways to determine the correct value for an empty cell:

If there is only one possible value based on rest of the cells or if there is one unique value in the possible values (If a cells possible values are like this: 1,2,3,2,3 based on the rest of the cells, it clearly tells it can hold either 1 or 2 or 3, Since, 1s occurrence is only once, it clearly shows that is the value it can hold). This is achieved by this function below:

/// <summary>
/// All possible values are sent here from zero cells.
/// This checks for unique value and returns it which is the correct value
/// </summary>
/// <param name="lStr"></param>
private void GetUniqueValue(string lStr)
{
    Array.Clear(lIntArray, 0, lIntArray.Length);//Clear the array
    Array.Clear(ldoubleIntArray, 0, ldoubleIntArray.Length);//Clear the array
    Array.Clear(ltripleIntArray, 0, ltripleIntArray.Length);//Clear the array

    int i = 0;
    int j = 0;
    int k = 0;
    Dictionary<char, int> dict = new Dictionary<char, int>();

    try
    {
        foreach (char ch in lStr)
        {
            if (dict.ContainsKey(ch))
                dict[ch] = dict[ch] + 1;
            else
                dict.Add(ch, 1);
        }
        foreach (KeyValuePair<char, int> m in dict)
        {
            if (m.Value == 1)// check for single occurence
            {
                //unique values in array is possible
                if (m.Key.ToString() != ":")
                {
                    lIntArray[i] = Int32.Parse(m.Key.ToString());
                    i++;
                }
            }
            else if (m.Value == 2)//check for double occurence
            {
                if (m.Key.ToString() != ":")
                {
                    ldoubleIntArray[j] = Int32.Parse(m.Key.ToString());
                    j++;
                }
            }
            else if (m.Value == 3)//check for triple occurence
            {
                if (m.Key.ToString() != ":")
                {
                    ltripleIntArray[k] = Int32.Parse(m.Key.ToString());
                    k++;
                }
            }
        }
    }
    catch (Exception e)
    {
        HasChanged = false;
        throw e;
    }
}

The possible values on the empty cells are updated using the below two methods:

UpdatePossValues(lvalue.ToString(), row.ToString(), col, false);          //To update the row
UpdatePossValues(lvalue.ToString(), col.ToString(), row, true);           //To update the col
UpdatePossValuesInQuarter(lvalue.ToString(), playArray[row, col].quarter);//To update in a 
                                                                          //quarter

The possible values after every iteration are printed on the rich textbox as this. Please see the if condition - isSource field is used to pick the possible values on the cells to be solved.

/// <summary>
/// To print possible solution in the Rich text boxes
/// </summary>
        private void PrintPossSolution()
        {
            for (int i = 0; i < noOfElementsInRowOrCol; i++)
            {
                for (int j = 0; j < noOfElementsInRowOrCol; j++)
                {
                    if (!playArray[i, j].isSource)
                    {
                        richTextBox1.AppendText("R" + i.ToString() + "C" + 
                        j.ToString() + ": " + playArray[i, j].posValue + Environment.NewLine);
                    }
                }
            }
        }

I have also added some more methods to solve using additional techniques if the usual way of solving doesn't give the complete answer.

SolvePossibleValuesRow2();  //check in Row for possible values with 2 occurences
SolvePossibleValuesCol2();  //check in Col for possible values with 2 occurences

For example, let’s assume in Q3, both the cells r4c0 and r4c1 has possible values which are 2,3, then, this gives a clue that both 2 and 3 can be there only in r4 and not in any other row in that quarter. With this clue, these 2 nos’, can be removed from r3 and r5 in that quarter. This will solve other empty cells by reducing the possible values. The same thing has been extended for column as well. These are called naked pairs.

The solution can be further extended for 3 cells in a quarter both row and col wise which is a scope for further development.

A fully solved puzzle is shown here. The no. 45 against each row and cols shows the count of the row and col. This is used to check whether the program has solved the solution or not.

The log shows the iteration taken to solve. Also, for every cell to be solved, it shows possible values. Here in this case as it is solved, each cell has only one value. In cases where the program could not solve, it shows the possible values - for e.g., R0C1: 5,6,7 which means R0C1 can have either 5 or 6 or 7.

Points of Interest

The naming convention of the textboxes was one of the good ways to get and assign the values back to the textbox. For more understanding on the naked pairs, please refer to the links below:

• https://www.thonky.com/sudoku/naked-pairs-triples-quads#:~:text=In%20sudoku%2C%20a%20naked%20pair,pair%20has%20to%20be%203.
• http://hodoku.sourceforge.net/en/tech_intersections.php

History

• 8^th June, 2020: Version 1.0 - Normal methods to solve
• 29^th June, 2020: Version 1.0 (no change) - Implemented Hidden naked pairs in possible solutions
• 20^th February, 2021: Version 1.1 - Implemented Brute Force method