ARC4 Encryption Library

Pavel Bashkardin

5.00/5 (15 votes)

10 Oct 2024MIT6 min read

36K

1.4K

ARC4 (Alleged RC4) Cryptography Provider Class Library

In this post, you will learn the details about the ARC4 algorithm and how to use the ARC4 encryption library in your project. You will see examples of encrypting and decrypting data, as well as an example of using a cryptographic stream.

Introduction

The ARC4 Cryptography Provider Class Library is a DLL file for .NET projects that includes an implementation of a well-known symmetric encryption algorithm that is not present in the System.Security.Cryptography namespace of the mscorlib library.

The cryptographic algorithm, known as ARC4 (Alleged RC4), is a stream cipher that is widely used in various information security systems on computer networks (for example, SSL and TLS protocols, WEP and WPA wireless security algorithms). The original RC4 stream cipher was created by Ronald Rivest of RSA Security. For seven years, the cipher was a trade secret, and the exact description of the algorithm was provided only after the signing of a non-disclosure agreement, but in September 1994 its description was anonymously sent to the mailing list of Cypherpunks.

To avoid potential claims from the trademark owner, the cipher is sometimes referred to as ARC4, meaning to alleged RC4 (since RSA Security did not officially release the algorithm).

Despite the fact that this cipher is not recommended, ARC4 remains popular due to its simplicity of software implementation and high speed of operation. Another important advantage is the variable key length and the same amount of encrypted and original data.

Library Contents

The library contains the folowing namepsaces:

System.Security.Cryptography includes an implementation of the SymmetricAlgorithm and DeriveBytes base classes for the ARC4 algorithm.
System.IO includes an implementation of a stream that contains encrypted data using ARC4 algorithm.

Usage

There are two ways to use ARC4Lib in your own project:

Copy the downloaded DLL file in a custom folder on your development folder. Create a project in Visual Studio IDE. In Solution Explorer, right-click on the References or Dependencies node and choose either Add Project Reference, then click the Browse button, select file ARC4Lib.dll to add, and then press OK.
Copy the downloaded source project in a custom folder on your development folder. Create a solution in Visual Studio IDE. Add a ARC4Lib.csproj to a solution. In Solution Explorer, right-click on the References or Dependencies node and choose either Add Project Reference then click Projects, select file ARC4Lib.csproj to add, and then press OK. In this way, you can modify ARC4Lib as you see fit.

To register the algorithm mapping names for the current application domain, try the following:

using System.Security.Cryptography;
// ...

ARC4.Register();

Example of Encryption and Decryption Data

using System.Security.Cryptography;
// ...

byte[] password = Encoding.UTF8.GetBytes("password");
byte[] data = Encoding.UTF8.GetBytes("secret");
byte[] encrypted, restored;
using (var arc4 = ARC4.Create(password)
{
   using(var transform = arc4.CreateEncryptor()) // Encryption.
   {
       encrypted = transform.TransformFinalBlock(data, 0, data.Length);
   }

   using(var transform = arc4.CreateDecryptor()) // Decryption.
   {
       restored = transform.TransformFinalBlock(data, 0, data.Length);
   }
}

Example of Using Cryptographic Stream

Shrink ▲

using System.Security.Cryptography;
// ...

string password = "password";
string data = "secret";
string restored;
using (var memory = new MemoryStream())
{
    // Encryption.
    using (var stream = new ARC4Stream(memory, password))
    {
        using (var writer = new StreamWriter(stream))
        {
            writer.Write(data);
        }
    }
    memory.Seek(0, SeekOrigin.Begin); // Reset the memory position to start.
    // Decryption.
    using (var stream = new ARC4Stream(memory, password))
    {
        using (var reader = new StreamReader(stream))
        {
            restored = reader.ReadToEnd();
        }
    }
}

Example of Forming a Key

using System.Security.Cryptography; 
// ... 

const int KEY_LENGTH = 64;
string password = "password";
byte[] key;
byte[] salt;
using (var deriveBytes = new ARC4DeriveBytes(password))
{
    key = deriveBytes.GetBytes(KEY_LENGTH);
    salt = deriveBytes.Salt;
}

How It Works

The core of the stream cipher algorithm consists of a function - a pseudo-random bit (gamma) generator, which produces a key bit stream (key stream, gamma, pseudo-random bit sequence). Then it is used for encryption, combining them with the original data using bitwise XOR; decryption is performed in a similar way (since XOR with the given data is an involution).

S-block Initialization

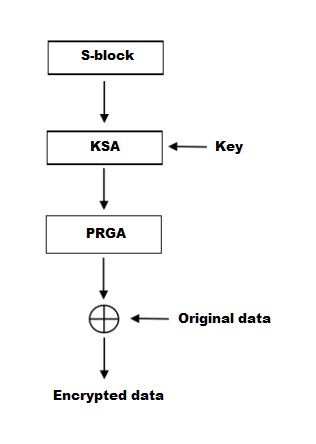
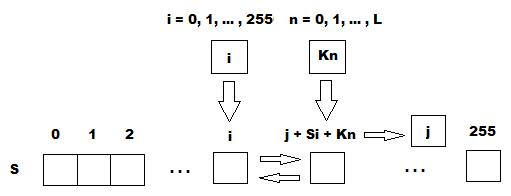
The algorithm is also known as the key-scheduling algorithm (KSA). This algorithm uses a key entered by the user, stored in Key, and has a length of L bytes. Initialization begins with filling the array (S-block), then this array is shuffled by permutations defined by the key. Since only one action is performed on S-block, the statement must be made that S-block always contains one set of values that was given during the initialization: S_i=i. The user can also enter his own version of the S-block using the initialization vector or generate a pseudo-random S-block.

byte[] sblock = new byte[256];    // The array contained S-block.
void CreateSBlock()
{
    for (int i = 0; i < 256; i++)
    {
        sblock[i] = (byte)i;      // S-block initialization.
    }
}
void KeyScheduling() (byte[] key) // KSA
{
    for (int i = 0, j = 0, l = key.Length; i < 256; i++)
    {
        j = (j + sblock[i] + key[i % l]) % 256;
        Swap(sblock, i, j);      // See below for "Swap" implementation ↓
    }
}

Attention! By default, in the current ARC4.Create() implementation the S-block is initialized with a pseudo-random byte array obtained using the linear congruential method (LCR) and random 256-bytes key. This does not quite correspond to the classical algorithm, when the S-block was initialized with a sequence from 0 to 255 (S_i=i) before being passed to PRGA. If classic behavior is required, use ARC4.Create(key) or pass ARC4SBlock.DefaultSBlock to ARC4.Create(key,iv) as an initialization vector. Otherwise, you should always keep the initialization vector to prevent corruption of the decrypted data, because the encrypted data will be different each time the engine is initialized by ARC4.Create().

If you want to use your own custom S-block, it will be tested with ValidBytes function to ensure that all 256 values are not duplicated.

bool ValidBytes(byte[] bytes)
{
    if (bytes == null || bytes.Length != 256)
    {
        return false;
    }
    for (int i = 0; i < 256; i++)
    {
        for (int j = i + 1; j < 256; j++)
        {
            if (bytes[i] == bytes[j])
            {
                return false;
            }
        }
    }
    return true;
}

Generating a Pseudo-Random Word K

This part of the algorithm is called the pseudo-random generation algorithm (PRGA). The ARC4 keystream generator permutes the values stored in S-block. In one ARC4 cycle, one 8-bit K word from the keystream is determined. In the future, the keyword will be added modulo two with the original text that the user wants to encrypt, and the encrypted text will be obtained.

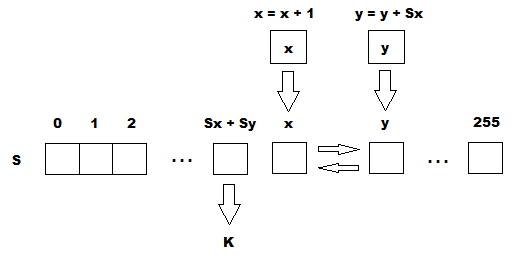
Function NextByte performs PRGA transformation and returns word K.

int x = 0, y = 0;
void Swap(byte[] array, int index1, int index2)
{
    byte b = array[index1];
    array[index1] = array[index2];
    array[index2] = b;
}
byte NextByte() // PRGA
{
    x = (x + 1) % 256;
    y = (y + sblock[x]) % 256;
    Swap(sblock, x, y);
    return sblock[(sblock[x] + sblock[y]) % 256];
}

Cipher Algorithm

Encryption

The function generates a sequence of bits K_i. The bit sequence is then combined with the original data D_i by a bitwise XOR (⊕) operation. The result is a cipher code C_i:

C_i = D_i ⊕ K_i.

Decryption

The key bitstream (keystream) K_i is re-created (regenerated). The bitstream of the key is added with the cipher C_i XOR operation. Due to the properties of the XOR operation, the output is the restored original data R_i (such that R_i = D_i for all i):

R_i = C_i ⊕ K_i = ( D_i ⊕ K_i ) ⊕ K_i

Function Cipher performs symmetric encryption and decryption using the ARC4 algorithm.

void Cipher(byte[] buffer, int offset, int count)
{
    for (int i = offset; i < count; i++)
    {
        buffer[i] = unchecked((byte)(buffer[i] ^ NextByte()));
    }
}

ARC4-based Random Bytes Generator

The ARC4DeriveBytes class implements the function of generating a key of a given length based on a password using the PRGA pseudo-random number generator. First, a data array of a given length is initialized by zero values, then it is filled using PRGA algorithm.

Linear Congruential Random

The essence of LCR method is to calculate a sequence of random numbers X_i, setting

X_i+1 = (A • X_i + C) MOD M, where:

M is the modulus, (a natural number M ≥ 2 relative to which it calculates the remainder of the division);
A is the factor (0 ≤ A < M);
C is the increment (0 ≤ C < M);
X₀ is the initial value 0 ≤ X₀ < M;
index i changes sequentially within 0 ≤ i < M.

Thus, LCR creates a sequence of M non-duplicate pseudo-random values only when:

the numbers С and M are coprime;
B = A - 1 multiple of P for every prime P that divides m;
B is a multiple of 4 if M is a multiple of 4.

For optimization in our case, it is predefined that:

X_i+1 = R ⊕ (A • X_i + C) MOD M,
Xi ∈ (0, 256),
X₀ is random,
R ∈ (0, 256) is random constant,
M = 256,
A ∈ (9, 249) and A - 1 can be divided by 4,
C ∈ (5, 251) and C is a prime number.

The upper bound for the number of distinct S-blocks that can be obtained using the following method is about 200 million values.

Shrink ▲

byte[] _A = // An array of all values that A.
{
    0x09, 0x0D, 0x11, 0x15, 0x19, 0x1D, 0x21, 0x25,
    0x29, 0x2D, 0x31, 0x35, 0x39, 0x3D, 0x41, 0x45,
    0x49, 0x4D, 0x51, 0x55, 0x59, 0x5D, 0x61, 0x65,
    0x69, 0x6D, 0x71, 0x75, 0x79, 0x7D, 0x81, 0x85,
    0x89, 0x8D, 0x91, 0x95, 0x99, 0x9D, 0xA1, 0xA5,
    0xA9, 0xAD, 0xB1, 0xB5, 0xB9, 0xBD, 0xC1, 0xC5,
    0xC9, 0xCD, 0xD1, 0xD5, 0xD9, 0xDD, 0xE1, 0xE5,
    0xE9, 0xED, 0xF1, 0xF5, 0xF9
};
byte[] _C = // An array of all values that C.
{
    0x05, 0x07, 0x0B, 0x0D, 0x11, 0x13, 0x17, 0x1D,
    0x1F, 0x25, 0x29, 0x2B, 0x2F, 0x35, 0x3B, 0x3D,
    0x43, 0x47, 0x49, 0x4F, 0x53, 0x59, 0x61, 0x65,
    0x67, 0x6B, 0x6D, 0x71, 0x7F, 0x83, 0x89, 0x8B,
    0x95, 0x97, 0x9D, 0xA3, 0xA7, 0xAD, 0xB3, 0xB5,
    0xBF, 0xC1, 0xC5, 0xC7, 0xD3, 0xDF, 0xE3, 0xE5,
    0xE9, 0xEF, 0xF1, 0xFB
};
void CreateRandomSBlock() // LCR
{
    using (RNGCryptoServiceProvider rng = new RNGCryptoServiceProvider())
    {
        byte[] random = new byte[4];
        rng.GetBytes(random);
        int r = random[0]; // For best ranodimzation.
        int x = random[1];
        int a = _A[random[2] % _A.Length];
        int c = _C[random[3] % _C.Length];
        int m = 256;
        for (int i = 0; i < m; i++)
        {
            // S-block initialization.
            sblock[i] = (byte) (r ^ (x = (a * x + c) % m));
        }
    }
}

↑ Back to contents.

License

This article, along with any associated source code and files, is licensed under The MIT License