This article describes the design, implementation and testing of a library to generate and display in Windows Forms various digital signals.
Introduction
Digital signals are commonly used to compress data. Storage of all the values of an analog signal on some medium over a certain range is practically impossible (just consider that the set of numbers between two real numbers, no matter how close they are, is infinite). Instead, samples are taken at regular time intervals and then stored for further processing. The C# library to generate and display digital signals will be described according to the order in which its constituent data structures and functions are needed. The attached ZIP file contains all the code.
Time and Magnitude Points
Digital signals are just sequences of time-magnitude points that are equally spaced in the time (horizontal) dimension. The following class will be used to keep track of data points.
public class TimeMagnitude
{
public double Time,
Magnitude;
public TimeMagnitude( double time, double magnitude )
{
Time = time; Magnitude = magnitude;
}
public TimeMagnitude Copy()
{
return new TimeMagnitude( this.Time, this.Magnitude );
}
}
In some applications, it is necessary to create a fresh copy of an existing TimeMagnitude instance. That is the purpose of function Copy.
Signal Parameters
In order to generate a digital signal, one must pretend that some samples are taken from the magnitude of the corresponding analog signal at regularly spaced time intervals. There are several parameters that must be specified for the proper generation of a signal, as defined in the following class. Most of the parameters are self-explanatory and some, such as frequency and period are redundant in the sense that if one is known, the other can be computed from it. The samplingFactor parameter is essential for the proper generation of a digital signal’s data points for further processing.
public class SignalParameters
{
public double amplitude, offset,
frequency,
period,
halfPeriod,
samplingFrequency,
frequencyResolution,
timeStep;
public int samplingFactor,
nSamples;
public SignalParameters( double _amplitude, double _frequency,
double _offset, int _nSamples, int _samplingFactor )
{
double one = (double)1.0;
amplitude =_amplitude;
frequency = _frequency;
samplingFactor = _samplingFactor;
nSamples = _nSamples;
offset = _offset;
period = one / frequency;
halfPeriod = period / (double)2.0;
samplingFrequency = (double)samplingFactor * frequency;
frequencyResolution = samplingFrequency / (double)nSamples;
timeStep = one / samplingFrequency;
}
}
Digital Signals
The generation of digital signals involves the simulation of sampling the magnitude of their corresponding analog signals at equally-spaced time points. In order to generate an arbitrary number of successive data points, the signal-generation functions can be implemented as enumerators that maintain their state from one call to the next. The signals to be generated are Sine, Cosine, Square, Sawtooth, Triangle and White noise.
Digital signals are generated by function members of the GeneratingFn class. The data members of this class are as follows:
public SignalParameters parameters;
public List<TimeMagnitude> sineSignalValues, cosineSignalValues,
squareSignalValues, sawtoothSignalValues,
triangleSignalValues, whiteNoiseValues;
public List<double> zeroCrossings;
private SignalPlot sineSignal, cosineSignal, squareSignal,
sawtoothSignal, triangleSignal, whiteNoise;
The constructor creates an instance of the class, initializing the signal parameters, the lists that will contain signal values, the list of zero crossings, and the signal plots:
public GeneratingFn( double _amplitude, double _frequency, double _offset = 0.0,
int _nSamples = 512, int _samplingFactor = 32 )
{
parameters = new SignalParameters( _amplitude, _frequency,
_offset, _nSamples, _samplingFactor );
sineSignalValues = new List<TimeMagnitude>();
cosineSignalValues = new List<TimeMagnitude>();
squareSignalValues = new List<TimeMagnitude>();
sawtoothSignalValues = new List<TimeMagnitude>();
triangleSignalValues = new List<TimeMagnitude>();
whiteNoiseValues = new List<TimeMagnitude>();
sineSignal = new SignalPlot( "sine-signal", SignalShape.sine );
sineSignal.Text = "Sine signal plot";
cosineSignal = new SignalPlot( "cosine-signal", SignalShape.cosine );
cosineSignal.Text = "Cosine signal plot";
squareSignal = new SignalPlot( "square-signal", SignalShape.square,
SignalContinuity.discontinuous );
squareSignal.Text = "Square signal plot";
sawtoothSignal = new SignalPlot( "sawtooth-signal", SignalShape.sawtooth,
SignalContinuity.discontinuous );
sawtoothSignal.Text = "Sawtooth signal plot";
triangleSignal = new SignalPlot( "triangle-signal", SignalShape.triangle );
triangleSignal.Text = "Triangle signal plot";
whiteNoise = new SignalPlot( "white-noise signal", SignalShape.whiteNoise );
whiteNoise.Text = "White noise plot";
}
In some applications, it is convenient to collect the magnitudes from a list of TimeMagnitude elements, which is simply accomplished as follows:
public double[] Magnitudes( List<TimeMagnitude> tmList )
{
double[] mags = null;
if ( tmList != null )
{
int n = tmList.Count;
mags = new double[ n ];
for ( int i = 0; i < n; ++i )
{
mags[ i ] = tmList[ i ].Magnitude;
}
}
return mags;
}
The constructor GeneratingFn and its public function members are called by a driver or user program. This will be illustrated later in this article by means of a test console application. The signal-generating functions are called repeatedly an arbitrary number of times. Each time they are called, the functions create a new TimeMagnitude element, add it to their corresponding list and return the double magnitude of such element.
Sine and Cosine Signals
The following enumerator is used to generate the elements of a Sine signal.
public IEnumerator<double> NextSineSignalValue()
{
double angularFreq = 2.0 * Math.PI * parameters.frequency;
double time = 0.0;
double wt, sinOFwt, magnitude = 0.0;
TimeMagnitude previousTM = null;
zeroCrossings = new List<double>();
while ( true )
{
try
{
wt = angularFreq * time;
sinOFwt = Math.Sin( wt );
magnitude = parameters.offset + ( parameters.amplitude * sinOFwt );
TimeMagnitude tm = new TimeMagnitude( time, magnitude );
sineSignalValues.Add( tm );
CheckZeroCrossing( previousTM, tm );
previousTM = tm.Copy();
}
catch ( Exception exc )
{
MessageBox.Show( exc.Message );
Abort();
}
yield return magnitude;
time += parameters.timeStep;
}
}
The function is defined as an IEnumerator. The first time it is called, it initializes its local variables and then goes into an infinite loop. If everything goes as expected inside the try-catch clause, the sineSignalValues list is updated and function CheckZeroCrossing is called to determine whether the signal has crossed the time axis.
private void CheckZeroCrossing( TimeMagnitude previousTM, TimeMagnitude tm )
{
if ( UtilFn.NearZero( tm.Magnitude ) )
{
zeroCrossings.Add( tm.Time );
}
else if ( previousTM != null && MagnitudeTransition( previousTM, tm ) )
{
zeroCrossings.Add( previousTM.Time + ( ( tm.Time - previousTM.Time ) / 2.0 ) );
}
}
A zero crossing may occur in three possible ways. In the best-case scenario, the signal magnitude may be very close to 0.0. However, due to the problems involved in the exact comparison of double numbers, the following utility code in class UtilFn defined in file Util_Lib.cs is used to compare a double against zero.
private static double fraction = (double)0.333333,
dTolerance = Math.Abs( fraction * (double)0.00001 ),
zero = (double)0.0;
public static bool EQdoubles( double d1, double d2 )
{
d1 = Math.Abs( d1 );
d2 = Math.Abs( d2 );
return Math.Abs( d1 - d2 ) <= dTolerance;
}
public static bool NearZero( double d )
{
return EQdoubles( d, zero );
}
The other two scenarios for a zero crossing to occur are either when the magnitude of the current TimeMagnitude element is below the time axis and the magnitude of previous one is above such axis, or when the magnitude of the previous TimeMagnitude element is below the time axis and the magnitude of the current one is above such axis. These scenarios are checked by the following function:
private bool MagnitudeTransition( TimeMagnitude previousTM, TimeMagnitude currentTM )
{
return ( previousTM.Magnitude > 0.0 && currentTM.Magnitude < 0.0 )
||
( previousTM.Magnitude < 0.0 && currentTM.Magnitude > 0.0 );
}
After checking for a zero crossing, the variable previousTM is updated, the function leaves the try-catch clause and executes yield return magnitude to return the signal value.
The next time the function is called, execution continues after the yield return statement, the time local variable is updated and the infinite loop continues. Observe that, in effect, the implementation of the function as an enumerator and the use of the yield return statement make the function’s local variables behave as the age-old C and C++ static variables. This is quite remarkable since, by design, C# does not support static variables.
If execution ever reaches the catch section of the try-catch clause, an exception has occurred. The function displays a MessageBox with the exception’s message and then calls function Abort to terminate the execution.
private void Abort()
{
if ( System.Windows.Forms.Application.MessageLoop )
{
System.Windows.Forms.Application.Exit();
}
else
{
System.Environment.Exit( 1 );
}
}
The generation of the next Cosine value is accomplished in a similar fashion, by calling Math.Cos instead of Math.Sin and will not be shown here. (Again, the complete code is in the attached ZIP file.)
Square Signals
The generation of a square signal is almost straightforward. The only difficulty is dealing with the vertical discontinuities, which must occur every time an auxiliary time variable t is near half of the signal period (parameters.halfPeriod).
public IEnumerator<double> NextSquareSignalValue()
{
double _amplitude = parameters.amplitude,
magnitude = parameters.offset + _amplitude;
double time = 0.0, t = 0.0;
bool updateZeroCrossings = magnitude > (double)0.0;
zeroCrossings = new List<double>();
while ( true )
{
try
{
TimeMagnitude tm = new TimeMagnitude( time, magnitude );
squareSignalValues.Add( new TimeMagnitude( time, magnitude ) );
}
catch ( Exception exc )
{
MessageBox.Show( exc.Message );
Abort();
}
yield return magnitude;
time += parameters.timeStep;
t += parameters.timeStep;
if ( UtilFn.NearZero( t - parameters.halfPeriod ) )
{
_amplitude = -_amplitude;
t = 0.0;
if ( updateZeroCrossings )
{
zeroCrossings.Add( time );
}
}
magnitude = parameters.offset + _amplitude;
}
}
Aside from dealing with the vertical discontinuities, the enumerator for square signals folllows the same logic as the enumerators for sine and cosine signals.
Sawtooth Signals
A sawtooth signal is generated by repeating a sloped straight line whose equation is:
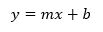
where m is the slope and b is the y-axis ordinate. Aside from the part dealing with the vertical discontinuity, the implementation of the corresponding enumerator is straightforward.
public IEnumerator<double> NextSawtoothSignalValue()
{
double m = 10.0 / parameters.period,
b = -parameters.amplitude;
double time = 0.0, t = 0.0;
double magnitude = 0.0;
TimeMagnitude previousTM, tm;
zeroCrossings = new List<double>();
while ( true )
{
previousTM = tm = null;
try
{
magnitude = parameters.offset + ( m * t + b );
tm = new TimeMagnitude( time, magnitude );
sawtoothSignalValues.Add( tm );
CheckZeroCrossing( previousTM, tm );
previousTM = tm.Copy();
}
catch ( Exception exc )
{
MessageBox.Show( exc.Message );
Abort();
}
yield return magnitude;
if ( UtilFn.NearZero( t - parameters.period ) )
{
t = 0.0;
if ( tm.Magnitude > (double)0.0 )
{
zeroCrossings.Add( time );
}
}
time += parameters.timeStep;
t += parameters.timeStep;
}
}
Observe that the vertical discontinuities of a sawtooth signal occur at multiples of the signal period.
Triangle Signals
A triangle signal can be viewed as two mirrored sloping lines from a sawtooth signal, an ascending line for the fist half of the period and a descending line for the second half of the period.
public IEnumerator<double> NextTriangleSignalValue()
{
double m = 10.0 / parameters.period,
b = -parameters.amplitude;
double time = 0.0, t = 0.0;
double magnitude = 0.0;
int j = 0;
TimeMagnitude previousTM, tm;
tm = previousTM = null;
bool mirror = false;
zeroCrossings = new List<double>();
while ( true )
{
try
{
if ( !mirror )
{
magnitude = parameters.offset + ( m * t + b );
tm = new TimeMagnitude( time, magnitude );
triangleSignalValues.Add( tm );
++j;
}
else
{
if ( j > 0 )
{
magnitude = triangleSignalValues[ --j ].Magnitude;
tm = new TimeMagnitude( time, magnitude );
triangleSignalValues.Add( tm );
}
}
}
catch ( Exception exc )
{
MessageBox.Show( exc.Message );
Abort();
}
CheckZeroCrossing( previousTM, tm );
previousTM = tm.Copy();
yield return magnitude;
if ( UtilFn.NearZero( t - parameters.halfPeriod ) )
{
mirror = true;
}
if ( UtilFn.NearZero( t - parameters.period ) )
{
t = 0.0;
j = 0;
mirror = false;
}
time += parameters.timeStep;
t += parameters.timeStep;
}
}
White Noise Signals
White noise is a random signal. Its data points occur at random according to a value obtained from a random number generator. In order to distribute the data points more or less evenly, two random number generators may be used: one for magnitudes and another for their sign.
public IEnumerator<double> NextWhiteNoiseSignalValue()
{
double magnitude = 0.0, time = 0.0, sign;
Random magRand, signRand;
magRand = new Random();
signRand = new Random();
zeroCrossings = new List<double>();
while ( true )
{
sign = ( signRand.Next( 10 ) > 5 ) ? 1.0 : -1.0;
magnitude = parameters.offset
+ sign * ( magRand.NextDouble() * parameters.amplitude );
whiteNoiseValues.Add( new TimeMagnitude( time, magnitude ) );
yield return magnitude;
time += parameters.timeStep;
}
}
This function initializes the list of zero crossings but never inserts elements into it. The reason is that white noise cannot be considered to correspond to a function such as sine, cosine, square, sawtooth or triangle, whose magnitude values follow a definite trend.
Signal Plots
The GeneratingFn class constructor initializes some private data members with instances of class SignalPlot, which are used to display Windows forms showing the data points of the generated signals. This class is defined in file SignalPlot.cs. There are two enumerations, one to specify the continuity of a signal and one to specify the shape of a signal.
public enum SignalContinuity { continuous, discontinuous };
public enum SignalShape { sine, cosine, square, sawtooth, triangle, whiteNoise };
The data members and the constructor of the class to create an instance of a Windows form to plot a signal are defined as follows:
public partial class SignalPlot : Form
{
private string description;
private SignalShape shape;
private SignalContinuity continuity;
private Bitmap bmp;
private int xAxis_Y,
sigMin_Y,
sigMax_Y;
private Graphics gr;
private Font drawFont;
private StringFormat drawFormat;
private int iScale,
iScaleDIV2;
private double dScale;
private int nextParameter_Y;
public SignalPlot( string _description, SignalShape _shape,
SignalContinuity _continuity = SignalContinuity.continuous )
{
InitializeComponent();
bmp = new Bitmap( pictureBox1.Width, pictureBox1.Height );
pictureBox1.Image = bmp;
gr = Graphics.FromImage( bmp );
gr.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;
gr.InterpolationMode = System.Drawing.Drawing2D.InterpolationMode.HighQualityBicubic;
gr.PixelOffsetMode = System.Drawing.Drawing2D.PixelOffsetMode.HighQuality;
gr.TextRenderingHint = System.Drawing.Text.TextRenderingHint.ClearTypeGridFit;
gr.Clear( Color.Transparent );
drawFont = new System.Drawing.Font( "Calibri", 10,
FontStyle.Regular, GraphicsUnit.Point );
drawFormat = new StringFormat();
description = _description;
shape = _shape;
continuity = _continuity;
xAxis_Y = bmp.Height / 2;
iScale = 10;
iScaleDIV2 = iScale / 2;
dScale = (double)iScale;
}
The constructor of the GeneratingFn class initializes several private data members (sineSignal, cosineSignal, squareSignal, sawtoothSignal, triangleSignal, and whiteNoiseSignal) with instances of class SignalPlot. Those instances can be used to plot the generated signals via the following functions that call function SignalPlot.Plot.
public void PlotSineSignal()
{
sineSignal.Plot( parameters, sineSignalValues );
}
public void PlotCosineSignal()
{
cosineSignal.Plot( parameters, cosineSignalValues );
}
public void PlotSquareSignal()
{
squareSignal.Plot( parameters, squareSignalValues, SignalContinuity.discontinuous );
}
public void PlotSawtoothSignal()
{
sawtoothSignal.Plot
( parameters, sawtoothSignalValues, SignalContinuity.discontinuous );
}
public void PlotTriangleSignal()
{
triangleSignal.Plot( parameters, triangleSignalValues );
}
public void PlotWhiteNoiseSignal()
{
whiteNoiseSignal.Plot( parameters, whiteNoiseValues );
}
The function to plot signals (SignalPlot.Plot) is pretty much straightforward. It takes as arguments the parameters of a signal, the list of time-magnitude points, and the continuity of the signal.
public void Plot( SignalParameters parameters, List<TimeMagnitude> list,
SignalContinuity continuity = SignalContinuity.continuous )
{
int n, m;
if ( list == null || ( n = list.Count ) == 0 )
{
MessageBox.Show(
String.Format( "No {0} values to plot", description ) );
}
else
{
int x, deltaX, currY, nextY;
sigMax_Y = 0;
sigMin_Y = bmp.Height;
Draw_X_axis();
Draw_Y_axis();
drawFormat.FormatFlags = StringFormatFlags.DirectionRightToLeft;
DrawParameters( parameters, shape );
deltaX = this.Width / n;
x = 0;
m = n - 2;
drawFormat.FormatFlags = StringFormatFlags.DirectionVertical;
for ( int i = 0; i < n; ++i )
{
int iScaledMag = ScaledMagnitude( list[ i ], dScale );
currY = xAxis_Y - iScaledMag;
if ( currY > sigMax_Y )
{
sigMax_Y = currY;
}
if ( currY < sigMin_Y )
{
sigMin_Y = currY;
}
if ( x >= bmp.Width )
{
break;
}
bmp.SetPixel( x, currY, Color.Black );
if ( UtilFn.IsDivisible( list[ i ].Time, parameters.period ) )
{
string label = String.Format( "___ {0:0.0000}", list[ i ].Time );
SizeF size = gr.MeasureString( label, drawFont );
gr.DrawString( label, drawFont, Brushes.Red,
new Point( x, bmp.Height - (int)size.Width ),
drawFormat );
}
if ( continuity == SignalContinuity.discontinuous && i <= m )
{
int iP1ScaledMag = ScaledMagnitude( list[ i + 1 ], dScale );
nextY = xAxis_Y - iP1ScaledMag;
if ( x > 0 && ( shape == SignalShape.square ||
shape == SignalShape.sawtooth ) )
{
if ( i < m )
{
CheckVerticalDiscontinuity( x, currY, nextY );
}
else
{
DrawVerticalDiscontinuity( x + deltaX, currY );
}
}
}
x += deltaX;
}
Draw_Y_axisNotches( parameters );
this.ShowDialog();
}
}
The function determines the maximum and minimum values for the Y coordinates, draws the signal parameters, sets pixels for the scaled magnitude data points and draws labels at X (time) coordinates that are divisible by the period of the signal, as determined by calling a utility function in file Util_Lib.cs.
public static bool IsDivisible( double x, double y )
{
return Math.Abs( ( ( Math.Round( x / y ) * y ) - x ) ) <= ( 1.0E-9 * y );
}
The reason for having used (twice) code in file Util_Lib.cs is that the author uses the functions in such a file in other applications. The file contains additional functions that have nothing to do with the generation and plotting of digital signals.
The functions called by function SignalPlot.Plot are pretty much self-explanatory. Most of them (Draw_X_axis, Draw_Y_axis, DrawParameters, ScaledMagnitude, Draw_Y_axisNotches, and DrawNotch) will not be described in the article.
Function DrawDelta_Y_X takes care of drawing the amplitude and time step of a signal. The time step is the reciprocal of the sampling frequency, which is the product of the sampling factor and the signal frequency. These parameters are crucial for the proper processing of digital signals in other applications.
private void DrawDelta_Y_X( SignalParameters parameters )
{
string delta_Y_X_str = String.Format( "deltaY: {0:00.000} V, time step: {1:0.00000} sec",
parameters.amplitude / 5.0, parameters.timeStep );
drawFormat.FormatFlags = StringFormatFlags.DirectionRightToLeft;
SizeF size = gr.MeasureString( delta_Y_X_str, drawFont );
int x = (int)size.Width + 8;
Point point = new Point( x, nextParameter_Y );
gr.DrawString( delta_Y_X_str, drawFont, Brushes.Red, point, drawFormat );
}
Two interesting functions are the ones that draw the vertical discontinuities of square and sawtooth signals. Before reaching the end of a square or sawtooth signal, it is necessary to check whether a discontinuity must be drawn. Furthermore, in the case of a square signal, the discontinuity must be drawn either going up or going down. For a sawtooth signal, the discontinuity always goes down.
private void CheckVerticalDiscontinuity( int x, int currY, int nextY )
{
if ( x >= bmp.Width )
{
return;
}
int discLength = Math.Abs( currY - nextY );
if ( discLength > iScaleDIV2 )
{
int y;
if ( currY < nextY )
{
for ( y = currY; y <= nextY; ++y )
{
bmp.SetPixel( x, y, Color.Black );
}
}
else
{
for ( y = currY; y >= nextY; --y )
{
bmp.SetPixel( x, y, Color.Black );
}
}
}
}
At the end of a square or a sawtooth signal, the discontinuity is drawn unconditionally.
private void DrawVerticalDiscontinuity( int x, int currY )
{
if ( x >= bmp.Width )
{
return;
}
int y;
if ( currY < sigMax_Y )
{
for ( y = currY; y <= sigMax_Y; ++y )
{
bmp.SetPixel( x, y, Color.Black );
}
}
else if ( currY > sigMin_Y )
{
for ( y = sigMin_Y; y <= currY; ++y )
{
bmp.SetPixel( x, y, Color.Black );
}
}
}
Testing the Signal-Generation Library
A simple console application can be written to test the signal-generation library. The code for this application is in file Program.cs in the TestSignalGenLib directory in the attached ZIP file. The Program class defines two private file-related variables to write the output sent to the command-prompt window of the console application. These variables are initialized in the Main function of the application as follows:
fs = new FileStream( @"..\..\_TXT\out.txt", FileMode.Create );
sw = new StreamWriter( fs );
The only public global variable is genFn. The Main function binds this variable to an instance of class GeneratingFn and then defines the enumerators to generate signals.
IEnumerator<double> Sine = genFn.NextSineSignalValue();
IEnumerator<double> Cosine = genFn.NextCosineSignalValue();
IEnumerator<double> Square = genFn.NextSquareSignalValue();
IEnumerator<double> Sawtooth = genFn.NextSawtoothSignalValue();
IEnumerator<double> Triangle = genFn.NextTriangleSignalValue();
IEnumerator<double> WhiteNoise = genFn.NextWhiteNoiseSignalValue();
All the signal generators are called a fixed number of times to enumerate and display signal values in the command-prompt window. Then, the time step and the zero crossings are displayed. Finally, the signal values are plotted in a Windows Form. For example, the following code corresponds to the case of a Sine signal.
int n = 512;
string signalName;
signalName = "Sine";
EnumerateValues( signalName, Sine, genFn.sineSignalValues, n );
DisplayTimeStepAndZeroCrossings( genFn, signalName );
genFn.PlotSineSignal();
At the end of the execution, the file @"..\..\_TXT\out.txt" contains all the text output that was sent to the command-prompt window of the console application. For brevity’s sake, only the first and the last periods of the signal are shown here. For ease of reference, the TimeMagnitude data points and the zero crossings are numbered.
Sine Signal Values
0 0.0000 0.0000 1 0.0003 0.9755 2 0.0006 1.9134 3 0.0009 2.7779
4 0.0013 3.5355 5 0.0016 4.1573 6 0.0019 4.6194 7 0.0022 4.9039
8 0.0025 5.0000 9 0.0028 4.9039 10 0.0031 4.6194 11 0.0034 4.1573
12 0.0038 3.5355 13 0.0041 2.7779 14 0.0044 1.9134 15 0.0047 0.9755
16 0.0050 0.0000
. . .
496 0.1550 0.0000 497 0.1553 -0.9755 498 0.1556 -1.9134 499 0.1559 -2.7779
500 0.1562 -3.5355 501 0.1566 -4.1573 502 0.1569 -4.6194 503 0.1572 -4.9039
504 0.1575 -5.0000 505 0.1578 -4.9039 506 0.1581 -4.6194 507 0.1584 -4.1573
508 0.1587 -3.5355 509 0.1591 -2.7779 510 0.1594 -1.9134 511 0.1597 -0.9755
Time step set by GeneratingFn constructor: 0.00031
Zero crossings found by GeneratingFn.NextSineSignalValue:
0 0.0000 1 0.0050 2 0.0052 3 0.0100 4 0.0150 5 0.0200 6 0.0250
7 0.0300 8 0.0350 9 0.0400 10 0.0450 11 0.0500 12 0.0550 13 0.0600
14 0.0650 15 0.0652 16 0.0700 17 0.0702 18 0.0750 19 0.0752 20 0.0800
21 0.0802 22 0.0850 23 0.0852 24 0.0900 25 0.0902 26 0.0950 27 0.0952
28 0.1000 29 0.1002 30 0.1050 31 0.1052 32 0.1100 33 0.1102 34 0.1150
35 0.1152 36 0.1200 37 0.1202 38 0.1250 39 0.1252 40 0.1300 41 0.1302
42 0.1350 43 0.1352 44 0.1400 45 0.1402 46 0.1450 47 0.1452 48 0.1500
49 0.1502 50 0.1550 51 0.1552
After displaying the signal values and the zero crossings in the command-prompt window, the application displays the signal plot as shown in the following figure:

The form is displayed in modal mode (by calling Form.ShowDialog in function SignalGenLib.Plot). As a second example, the following figure shows the plot of a 500-Hz sine signal. The zero crossings are listed under the figure:

Zero crossings found by GeneratingFn.NextSineSignalValue:
0 0.0000 1 0.0010 2 0.0020 3 0.0030 4 0.0040 5 0.0050 6 0.0060
7 0.0070 8 0.0080 9 0.0090 10 0.0100 11 0.0110 12 0.0120 13 0.0130
14 0.0140 15 0.0150 16 0.0160 17 0.0170 18 0.0180 19 0.0190 20 0.0200
21 0.0210 22 0.0220 23 0.0230 24 0.0240 25 0.0250 26 0.0260 27 0.0270
28 0.0280 29 0.0290 30 0.0300 31 0.0310
Observe that even though the 100 Hz and the 500 Hz sine signals look identical, they are not because the time-axis marks have different values. Furthermore, due to their different frequencies, the first signal crosses the time axis 52 times, while the second one crosses the axis 32 times.
When a Windows Form is closed by clicking on its upper-right corner cross, the program runs similar code to generate plots of Cosine, Square, Sawtooth, Triangle and White noise signals with the same parameters used to generate the Sine signal. Each time a signal plot is displayed, it must be closed to generate and display the next one. The following two figures show the plots for the Square and White noise signals.


The command-prompt window indicates that there are no zero crossings in the case of White noise. This is because white noise is not like all the other discrete signals, for which adjacent points follow a regular trend.
As an additional example, the following figure shows a 100Hz Triangle signal having an amplitude of 6 volts and a DC offset of 2.5 volts, which is generated by the code:
genFn = new GeneratingFn( 6.0, 100.0, 2.5 );
IEnumerator<double> Triangle = genFn.NextTriangleSignalValue();
signalName = "Triangle";
EnumerateValues( signalName, Triangle, genFn.triangleSignalValues, n );
DisplayTimeStepAndZeroCrossings( genFn, signalName );
genFn.PlotTriangleSignal();

Using the Code
The attached ZIP file contains eight files in three directories. The Util_Lib directory contains file UtilFn.cs. The SignalGenLib directory contains files GeneratingFn.cs, SignalParameters.cs, SignalPlot.cs, SignalPlot.Designer.cs, SignalPlot.resx and TimeMagnitude.cs. The TestSignalGenLib directory contains file Program.cs.
Create a directory “Generation of Digital Signals”. In Visual Studio, click on “File”, select “New”, and click on “Project”. Select “Class Library”, specify the directory created as the “Location”, and the “Name” as “Util_Lib”. In the Solution Explorer pane, right click on "Class1.cs", select "Rename" and change the class name to "UtilFn.cs". Copy the code from file “UtilFn.cs” in the attached ZIP file to the “UtilFn.cs” file created. Click on "Build" and then on "Build Solution". The build should succeed. Click on "File" and then on "Close Solution".
Repeat the previous steps to create a library named “SignalGenLib”. In the Solution Explorer pane, right click on "Class1.cs", select "Rename" and change the class name to "GeneratingFn.cs". Right-click on "References", select "Add Reference", click on the ".NET" tab, select "System.Windows.Forms" and click on "OK"; do the same to add a reference to "System.Drawing". Right-click on "References", select "Add Reference", click on the "Browse" tab, navigate to the directory “Util_Lib\bin\Debug”, select "Util_Lib.dll" and click on "OK". Replace the entire contents of the "GeneratingFn.cs" file just created with the contents of the attached "GeneratingFn.cs" file. Select "File" and click on "Save All".
Copy the files "SignalParameters.cs", "SignalPlot.cs", "SignalPlot.Designer.cs", "SignalPlot.resx" and "TimeMagnitude.cs" to the "SignalGenLib" directory. For each of the copied files, in the Solution Explorer pane, right click on "SignalGenLib", select, "Add", click on "Existing Item", select the file to be added and click on "Add". The Error List pane should indicate 0 Errors, 0 Warnings and 0 Messages. Click on the "Build" tab and then on "Build Solution". The build should succeed. Click on "File" and then on "Close Solution".
Click on “File”, select “New”, and click on “Project”, select “Console Application”, with name “TestSignalGenLib”. In the Solution Explorer, right-click on "References", click on "Add Reference", click on the "Browse" tab, navigate to the directory “SignalGenLib\bin\Debug”, select "SignalGenLib.dll" and click on "OK”. Click on “File” and then on “Save All”. Add a reference to “SignalGenLib.dll”. Replace the entire contents of the file with the entire contents of the attached "Program.cs" file. Click on "Build" and then on "Build Solution". The build should succeed. Create a directory named "_TXT" under the "TestSignalGenLib" directory. Click on "Debug" and then on "Start Without Debugging". The console application should generate signal values and display a plot for each of the signals. Close the current Windows-form plot to generate the values of the next signal and display its plot. After closing the White noise plot, press any key to exit the console application.
Conclusion
This article has dealt with the design, implementation and testing of a C# library to generate and display some common digital signals. The signal-generation functions were implemented as enumerators which, by the use of yield return, in effect maintain the state of their local variables between successive calls. The library will be used again to test the implementation of a digital Biquad Bandpass Filter. The results of such a test will be reported in a forthcoming article.
History
- 2nd March, 2022: Initial version
