The code includes five classes in order to evaluate a string of a real, complex or polynomial math expression, perhaps reducing the expression to one real or complex number or an equivalent polynomial. The math expression may or may not include variables.


Introduction
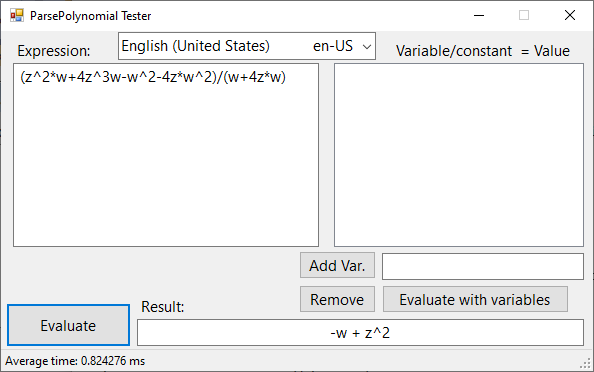
In many situations, there may be a string containing a math expression, such as "1+2*5", "(3+i)(3-i)" or "(z^2*w+4z^3w-w^2-4z*w^2)/(w+4z*w)", and there is the need to do the math and calculate the result. Maybe we need to calculate the result for different variables values and the result can be another polynomial. In those cases, the polynomials' parser presented here may help.
Background
The classes here are a small part -but improved- of my all free and downloadable CAS calculator. One of the goals is that these classes do not rely on other 'external' classes as happens in the CAS calculator.
The Seven Classes
-
Class 'Msg10' just contains a few messages to handle possible errors.
- Class '
G10' holds global members like Regex patterns. -
Class 'Rational' gives a bit more of accuracy in the operations.
-
Class 'Complex' does the complex math.
-
Class 'Polynomial' operates polynomials.
- Class '
Roots' finds polynomials' roots and factors. -
Class 'parsePolynomial' is in charge of dividing the input string into tokens and call accordingly to Roots, Polynomial or Msg10 classes. Roots depends on Polynomial class which, in turn, depends on Complex and Complex on Rational. The 'tokenizing' job is done by a Regex pattern.
Tokens
The tokens groups are:
numbers <num>
operators <op>
logical operators <lop>
functions <fn>
functions <vfn> functions retreiving a complex or polynomial array
constants <cnt>
variables <var>
any other character <any>
besides end of tokens <end> formed by an escape character Chr(27).
The pattern looks like:
(?s)(?<num>((\d{1,3}((\,\d{3})+(?!\d))(\.[0-9]+)?)|[\.\d]+)([eE](\s*)[-+]?[0-9]+)?)(?-s)|
(?<op>[-+*/\^])|
(?<lop>nand|mod|and|nor|xor|not|or|%|!)(?![a-zA-Z_]+)|
(?i)(?<fn>logtwo|logten|acosh|acoth|acsch|asech|asinh|atanh|floor|round|norm|conj|
coth|csch|sech|acos|acot|acsc|asec|asin|atan|cosh|sign|sinh|sqrt|tanh|abs|cos|cot|
csc|exp|log|sec|sin|sqr|tan|ln|re|im(?-i))(?![a-zA-Z_]+)|
(?i)(?<vfn>roots|(?<fct>factorize|factors|factor)(?-i))(?![a-zA-Z_]+)|
(?<cnt>e|(?i)pi(?-i))(?![a-zA-Z_]+)|
\(|\)|
(?<vars>\w)+|(?<end>\e)+|
(?<any>[^\s←\,\.])+|(?<any>\,|\.)+
The trailing '(?![a-zA-Z_]+)' in, for example, <cnt> allows to use variables like 'epsilon' or 'cosA' without interfering with constants, logical operators and functions.
Function roots returns an array of complex numbers containg the roots of the input polynomial. Function factor returns an array of the input polynomial's factors. The input can also be in the form (numerator polynomial)/(denominator polynomial).
Using the Code
The are two possible ways of instantiation:
Dim eP As New ParsePolynomial
eP.CultureInfo = New Globalization.CultureInfo("fr-FR")
...
Dim eP As New ParsePolynomial(New Globalization.CultureInfo("es-AR"))
...
By default, CultureInfo is set to "en-US".
Evaluation is done by calling one of the two Evaluate() methods.
First method:
Dim poly As Polynomial = eP.Evaluate("(x-1)*(x+1)")
...
First method with variables, set in a Dictionary(Of String, Polynomial):
Dim eP As New ParsePolynomial
eP.vars.Add("x", New Polynomial(Complex.one))
Dim polyA As New Polynomial("a", 2)
polyA += New Polynomial(-1.0)
eP.vars.Add("y", polyA)
Dim cplx As Complex = eP.Evaluate("x*(y-i*5)")
...
Once the string has been parsed, it is possible to call the overloaded second method:
eP.vars.Item("x") = New Polynomial(3)
Dim polyC As Polynomial = eP.Evaluate(eP.vars)
...
Variables names start with a letter or underscore (_), can contain letters, numbers or underscore and can be any length.
Of course, you may call directly to the Polynomial class, if you don't need the parser.
The Output
The output can be just one Polynomial, a Complex() array , or Polynomial() array :
Dim t1 As Int64 = Now.Ticks
Dim p As Polynomial = eP.Evaluate(TBExpression.Text)
Dim t2 As New TimeSpan(Now.Ticks - t1)
If eP.vPoly.Length Then
Dim s1 As String = ""
For i As Int32 = 0 To eP.vPoly.Length - 1
If eP.vPoly(i) IsNot Nothing Then
s1 += eP.vPoly(i).ToStringPolynomial(eP.Decimals, eP.Imaginary, eP.CultureInfo) + "</br>"
Else
s1 += "-------------------</br>"
End If
Next
NavigateToString(s1)
ElseIf eP.vRoots.Length Then
Dim s1 As String = ""
For i As Int32 = 0 To eP.vRoots.Length - 1
s1 += eP.vRoots(i).ToStringComplex(eP.Decimals, eP.Imaginary, eP.CultureInfo) + "</br>"
Next
NavigateToString(s1)
Else
NavigateToString(p.ToStringPolynomial(eP.Decimals, eP.Imaginary, eP.CultureInfo))
End If
When calling eP.Evaluate("factor(numerator)/(denominator)") the return will be in eP.vPoly() and a null element will separate factors from the numerator and the denominator.
You may call Polynomial.ToString() or ToStringPolynomial(Optional numDecimals As Int32 = 15, Optional sImg As String = "i", Optional cultureInfo As Globalization.CultureInfo = Nothing) As String:
...
polyC.ToStringPolynomial(4, eP.Imaginary, eP.CultureInfo)
...


Detail Version
The detail version will show operation steps by prepending the word 'detail'.

Basic Principles
The parsing method is a recursive-descent parsing: Parsing Expressions by Recursive Descent.
Evaluation method E calls T for any addition or subtraction, but T calls first F for any multiplication or subtraction, and F calls first P for any power possible power operation. P calls first v to get next token. If there is a "(" token, v calls recursively to T.
E --> T {( "+" | "-" ) T}
T --> F {( "*" | "/" ) F}
F --> P ["^" F]
P --> v | "(" E ")" | "-" T
Step by Step Walk-throughs
Algorithm presented here englobes T and F in a single method. Besides, method v operates any possible function like cos(), csc(), mod and so on.
While writing this article, I found some glitches. If you find any further error, please let me know.
History
- 3rd April, 2022: Initial version
