How to use multi indexing in Pandas process multi dimensional data, with practical use cases such as monitoring sports performance data and rises in earth surface temperatures.
Introduction
Pandas is a widely used data manipulation library in Python that offers extensive capabilities for handling various types of data. One of its notable features is the ability to work with MultiIndexes, also known as hierarchical indexes. In this blog post, we will delve into the concept of MultiIndexes and explore how they can be leveraged to tackle complex, multidimensional datasets.
Understanding MultiIndexes: Analyzing Sports Performance Data
A MultiIndex is a Pandas data structure that allows indexing and accessing data across multiple dimensions or levels. It enables the creation of hierarchical structures for rows and columns, providing a flexible way to organize and analyze data. To illustrate this, let's consider a scenario where you are a personal trainer or coach monitoring the health parameters of your athletes during their sports activities. You want to track various parameters such as heart rate, running pace, and cadence over a specific time interval.
Synthetic Health Performance Data
To work with this type of data, let's begin by writing Python code that simulates health performance data, specifically heart rates and running cadences:
from __future__ import annotations
from datetime import datetime, timedelta
import numpy as np
import pandas as pd
start = datetime(2023, 6, 8, 14)
end = start + timedelta(hours=1, minutes=40)
timestamps = pd.date_range(start, end, freq=timedelta(minutes=1), inclusive='left')
def get_heart_rate(begin_hr: int, end_hr: int, break_point: int) -> pd.Series[float]:
noise = np.random.normal(loc=0.0, scale=3, size=100)
heart_rate = np.concatenate((np.linspace(begin_hr, end_hr, num=break_point),
[end_hr] * (100 - break_point))) + noise
return pd.Series(data=heart_rate, index=timestamps)
def get_cadence(mean_cadence: int) -> pd.Series[float]:
noise = np.random.normal(loc=0.0, scale=1, size=100)
cadence = pd.Series(data=[mean_cadence] * 100 + noise, index=timestamps)
cadence[::3] = np.NAN
cadence[1::3] = np.NAN
return cadence.ffill().fillna(mean_cadence)
The code snippet provided showcases the generation of synthetic data for heart rate and cadence during a sports activity. It begins by importing the necessary modules such as datetime, numpy, and pandas.
The duration of the sports activity is defined as 100 minutes, and the **pd.date_range** function is utilized to generate a series of timestamps at one-minute intervals to cover this period.
The get_heart_rate function generates synthetic heart rate data, assuming a linear increase in heart rate up to a certain level, followed by a constant level for the remainder of the activity. Gaussian noise is introduced to add variability to the heart rate data, making it more realistic.
Similarly, the get_cadence function generates synthetic cadence data, assuming a relatively constant cadence throughout the activity. Gaussian noise is added to create variability in the cadence values, with the noise values being updated every three minutes instead of every minute, reflecting the stability of cadence compared to heart rates.
With the data generation functions in place, it is now possible to create synthetic data for two athletes, Bob and Alice:
bob_hr = get_heart_rate(begin_hr=110, end_hr=160, break_point=20)
alice_hr = get_heart_rate(begin_hr=90, end_hr=140, break_point=50)
bob_cadence = get_cadence(mean_cadence=175)
alice_cadence = get_cadence(mean_cadence=165)
At this point, we have the heart rates and cadences of Bob and Alice. Let's plot them using matplotlib to get some more insight into the data:
from __future__ import annotations
import matplotlib.dates as mdates
import matplotlib.pyplot as plt
date_formatter = mdates.DateFormatter('%H:%M:%S')
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(111)
ax.xaxis.set_major_formatter(date_formatter)
ax.plot(bob_hr, color="red", label="Heart Rate Bob", marker=".")
ax.plot(alice_hr, color="red", label="Heart Rate Alice", marker="v")
ax.grid()
ax.legend()
ax.set_ylabel("Heart Rate [BPM]")
ax.set_xlabel("Time")
ax_cadence = ax.twinx()
ax_cadence.plot(bob_cadence, color="purple",
label="Cadence Bob", marker=".", alpha=0.5)
ax_cadence.plot(alice_cadence, color="purple",
label="Cadence Alice", marker="v", alpha=0.5)
ax_cadence.legend()
ax_cadence.set_ylabel("Cadence [SPM]")
ax_cadence.set_ylim(158, 180)
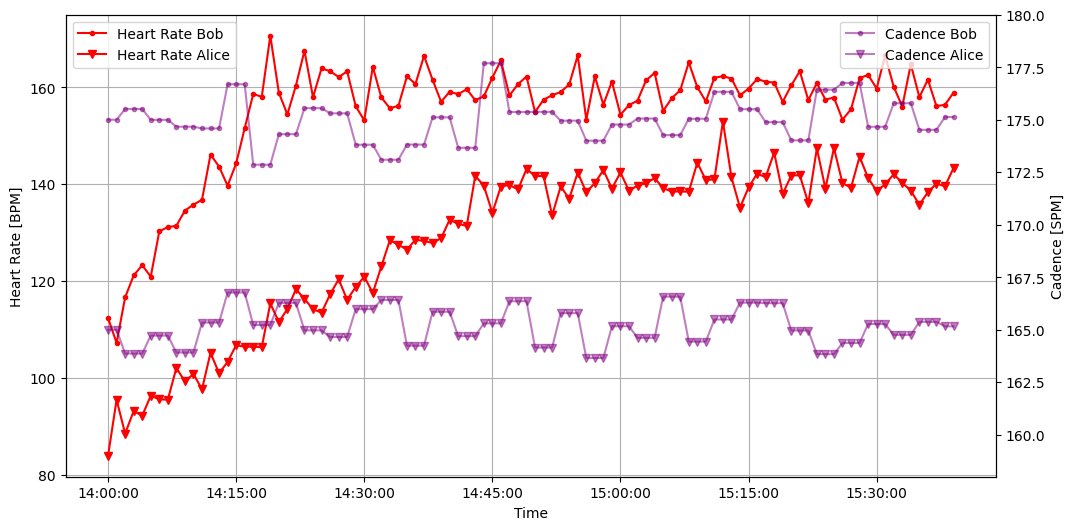
Great! The initial analysis of the data provides interesting observations. We can easily distinguish the differences between Bob and Alice in terms of their maximum heart rate and the rate at which it increases. Additionally, Bob's cadence appears to be notably higher than Alice's.
Using Dataframes for Scalability
However, as you might have already noticed, the current approach of using separate variables (bob_hr, alice_hr, bob_cadence, and alice_cadence) for each health parameter and athlete is not scalable. In real-world scenarios with a larger number of athletes and health parameters, this approach quickly becomes impractical and cumbersome.
To address this issue, we can leverage the power of pandas by utilizing a pandas DataFrame to represent the data for multiple athletes and health parameters. By organizing the data in a tabular format, we can easily manage and analyze multiple variables simultaneously.
Each row of the DataFrame can correspond to a specific timestamp, and each column can represent a health parameter for a particular athlete. This structure allows for efficient storage and manipulation of multidimensional data.
By using a DataFrame, we can eliminate the need for separate variables and store all the data in a single object. This enhances code clarity, simplifies data handling, and provides a more intuitive representation of the overall dataset.
bob_df = pd.concat([bob_hr.rename("heart_rate"),
bob_cadence.rename("cadence")], axis="columns")
This is what the Dataframe for Bob’s health data looks like:
| | heart_rate | cadence |
2023-06-08 14:00:00 | 112.359 | 175 |
2023-06-08 14:01:00 | 107.204 | 175 |
2023-06-08 14:02:00 | 116.617 | 175.513 |
2023-06-08 14:03:00 | 121.151 | 175.513 |
2023-06-08 14:04:00 | 123.27 | 175.513 |
2023-06-08 14:05:00 | 120.901 | 174.995 |
2023-06-08 14:06:00 | 130.24 | 174.995 |
2023-06-08 14:07:00 | 131.15 | 174.995 |
2023-06-08 14:08:00 | 131.402 | 174.669 |
Introducing Hierarchical Dataframes
The last dataframe looks better already! But now, we still have to create a new dataframe for each athlete. This is where pandas MultiIndex can help. Let's take a look at how we can elegantly merge the data of multiple athletes and health parameters into one dataframe:
from itertools import product
bob_df = bob_hr.to_frame("value")
bob_df["athlete"] = "Bob"
bob_df["parameter"] = "heart_rate"
values = {
"Bob": {
"heart_rate": bob_hr,
"cadence": bob_cadence,
},
"Alice": {
"heart_rate": alice_hr,
"cadence": alice_cadence
}
}
sub_dataframes: list[pd.DataFrame] = []
for athlete, parameter in product(["Bob", "Alice"], ["heart_rate", "cadence"]):
sub_df = values[athlete][parameter].to_frame("values")
sub_df["athlete"] = athlete
sub_df["parameter"] = parameter
sub_dataframes.append(sub_df)
df = pd.concat(sub_dataframes).set_index(["athlete", "parameter"], append=True)
df.index = df.index.set_names(["timestamps", "athlete", "parameter"])
This code processes heart rate and cadence data for athletes, Bob and Alice. It performs the following steps:
- Create a
DataFrame for Bob's heart rate data and add metadata columns for athlete and parameter. - Define a dictionary that stores heart rate and cadence data for Bob and Alice.
- Generate combinations of athletes and parameters (Bob/Alice and heart_rate/cadence).
- For each combination, create a sub-dataframe with the corresponding data and metadata columns.
- Concatenate all sub-dataframes into a single dataframe.
- Set the index to include levels for timestamps, athlete, and parameter. This is where the actual
MultiIndex is created
This is what the hierarchical dataframe df looks like:
| | values |
(Timestamp('2023-06-08 14:00:00'), 'Bob', 'heart_rate') | 112.359 |
(Timestamp('2023-06-08 14:01:00'), 'Bob', 'heart_rate') | 107.204 |
(Timestamp('2023-06-08 14:02:00'), 'Bob', 'heart_rate') | 116.617 |
(Timestamp('2023-06-08 14:03:00'), 'Bob', 'heart_rate') | 121.151 |
(Timestamp('2023-06-08 14:04:00'), 'Bob', 'heart_rate') | 123.27 |
(Timestamp('2023-06-08 14:05:00'), 'Bob', 'heart_rate') | 120.901 |
(Timestamp('2023-06-08 14:06:00'), 'Bob', 'heart_rate') | 130.24 |
(Timestamp('2023-06-08 14:07:00'), 'Bob', 'heart_rate') | 131.15 |
(Timestamp('2023-06-08 14:08:00'), 'Bob', 'heart_rate') | 131.402 |
At this point, we have got ourselves a single dataframe that holds all information for an arbitrary amount of athletes and health parameters. We can now easily use the .xs method to query the hierarchical dataframe:
df.xs("Bob", level="athlete")
| | values |
(Timestamp('2023-06-08 14:00:00'), 'heart_rate') | 112.359 |
(Timestamp('2023-06-08 14:01:00'), 'heart_rate') | 107.204 |
(Timestamp('2023-06-08 14:02:00'), 'heart_rate') | 116.617 |
(Timestamp('2023-06-08 14:03:00'), 'heart_rate') | 121.151 |
(Timestamp('2023-06-08 14:04:00'), 'heart_rate') | 123.27 |
df.xs("heart_rate", level="parameter") *
| | values |
(Timestamp('2023-06-08 14:00:00'), 'Bob') | 112.359 |
(Timestamp('2023-06-08 14:01:00'), 'Bob') | 107.204 |
(Timestamp('2023-06-08 14:02:00'), 'Bob') | 116.617 |
(Timestamp('2023-06-08 14:03:00'), 'Bob') | 121.151 |
(Timestamp('2023-06-08 14:04:00'), 'Bob') | 123.27 |
df.xs("Bob", level="athlete").xs
("heart_rate", level="parameter")
| timestamps | values |
2023-06-08 14:00:00 | 112.359 |
2023-06-08 14:01:00 | 107.204 |
2023-06-08 14:02:00 | 116.617 |
2023-06-08 14:03:00 | 121.151 |
2023-06-08 14:04:00 | 123.27 |
Use Case: Earth Temperature Changes
To demonstrate the power of hierarchical dataframes, let's explore a real-world and complex use case: analyzing the changes in Earth's surface temperatures over the last decades. For this task, we'll utilize a dataset available on Kaggle, which summarizes the Global Surface Temperature Change data distributed by the National Aeronautics and Space Administration Goddard Institute for Space Studies (NASA-GISS).
Inspect and Transform Original Data
Let's begin by reading and inspecting the data. This step is crucial to gain a better understanding of the dataset's structure and contents before delving into the analysis. Here's how we can accomplish that using pandas:
from pathlib import Path
file_path = Path() / "data" / "Environment_Temperature_change_E_All_Data_NOFLAG.csv"
df = pd.read_csv(file_path , encoding='cp1252')
df.describe()

Click on image for full size
From this initial inspection, it becomes evident that the data is organized in a single dataframe, with separate rows for different months and countries. However, the values for different years are spread across several columns in the dataframe, labeled with the prefix 'Y'. This format makes it challenging to read and visualize the data effectively. To address this issue, we will transform the data into a more structured and hierarchical dataframe format, enabling us to query and visualize the data more conveniently.
from dataclasses import dataclass, field
from datetime import date
from pydantic import BaseModel
MONTHS = {
"January": 1,
"February": 2,
"March": 3,
"April": 4,
"May": 5,
"June": 6,
"July": 7,
"August": 8,
"September": 9,
"October": 10,
"November": 11,
"December": 12
}
class GistempDataElement(BaseModel):
area: str
timestamp: date
value: float
@dataclass
class GistempTransformer:
temperature_changes: list[GistempDataElement] = field(default_factory=list)
standard_deviations: list[GistempDataElement] = field(default_factory=list)
def _process_row(self, row) -> None:
relevant_elements = ["Temperature change", "Standard Deviation"]
if (element := row["Element"]) not in relevant_elements or
(month := MONTHS.get(row["Months"])) is None:
return None
for year, value in row.filter(regex="Y.*").items():
new_element = GistempDataElement(
timestamp=date(year=int(year.replace("Y", "")), month=month, day=1),
area=row["Area"],
value=value
)
if element == "Temperature change":
self.temperature_changes.append(new_element)
else:
self.standard_deviations.append(new_element)
@property
def df(self) -> pd.DataFrame:
temp_changes_df = pd.DataFrame.from_records([elem.dict()
for elem in self.temperature_changes])
temp_changes = temp_changes_df.set_index
(["timestamp", "area"]).rename(columns={"value": "temp_change"})
std_deviations_df = pd.DataFrame.from_records([elem.dict()
for elem in self.standard_deviations])
std_deviations = std_deviations_df.set_index
(["timestamp", "area"]).rename(columns={"value": "std_deviation"})
return pd.concat([temp_changes, std_deviations], axis="columns")
def process(self):
environment_data = Path() / "data" /
"Environment_Temperature_change_E_All_Data_NOFLAG.csv"
df = pd.read_csv(environment_data, encoding='cp1252')
df.apply(self._process_row, axis="columns")
This code introduces the GistempTransformer class, which demonstrates the processing of temperature data from a CSV file and the creation of a hierarchical DataFrame containing temperature changes and standard deviations.
The GistempTransformer class, defined as a dataclass, includes two lists, temperature_changes and standard_deviations, to store the processed data elements. The _process_row method is responsible for handling each row of the input DataFrame. It checks for relevant elements, such as "Temperature change" and "Standard Deviation," extracts the month from the Months column, and creates instances of the GistempDataElement class. These instances are then appended to the appropriate lists based on the element type.
The df property returns a DataFrame by combining the temperature_changes and standard_deviations lists. This hierarchical DataFrame has a MultiIndex with levels representing the timestamp and area, providing a structured organization of the data.
transformer = GistempTransformer()
transformer.process()
df = transformer.df
| | temp_change | std_deviation |
(datetime.date(1961, 1, 1), 'Afghanistan') | 0.777 | 1.95 |
(datetime.date(1962, 1, 1), 'Afghanistan') | 0.062 | 1.95 |
(datetime.date(1963, 1, 1), 'Afghanistan') | 2.744 | 1.95 |
(datetime.date(1964, 1, 1), 'Afghanistan') | -5.232 | 1.95 |
(datetime.date(1965, 1, 1), 'Afghanistan') | 1.868 | 1.95 |
Analyzing Climate Data
Now that we have consolidated all the relevant data into a single dataframe, we can proceed with inspecting and visualizing the data. Our focus is on examining the linear regression lines for each area, as they provide insights into the overall trend of temperature changes over the past decades. To facilitate this visualization, we will create a function that plots the temperature changes along with their corresponding regression lines.
def plot_temperature_changes(areas: list[str]) -> None:
fig = plt.figure(figsize=(12, 6))
ax1 = fig.add_subplot(211)
ax2 = fig.add_subplot(212)
for area in areas:
df_country = df[df.index.get_level_values("area") == area].reset_index()
dates = df_country["timestamp"].map(datetime.toordinal)
gradient, offset = np.polyfit(dates, df_country.temp_change, deg=1)
ax1.scatter(df_country.timestamp, df_country.temp_change, label=area, s=5)
ax2.plot(df_country.timestamp, gradient * dates + offset, label=area)
ax1.grid()
ax2.grid()
ax2.legend()
ax2.set_ylabel("Regression Lines [°C]")
ax1.set_ylabel("Temperature change [°C]")
In this function, we are using the **get_level_values** method on a pandas MultiIndex to efficiently query the data in our hierarchical Dataframe on different levels. Let's use this function to visualize temperature changes in the different continents:
plot_temperature_changes
(["Africa", "Antarctica", "Americas", "Asia", "Europe", "Oceania"])

From this plot, we can draw several key conclusions:
- The regression lines for all continents have a positive gradient, indicating a global trend of increasing Earth surface temperatures.
- The regression line for Europe is notably steeper compared to other continents, implying that the temperature increase in Europe has been more pronounced. This finding aligns with observations of accelerated warming in Europe compared to other regions.
- The specific factors contributing to the higher temperature increase in Europe compared to Antarctica are complex and require detailed scientific research. However, one contributing factor may be the influence of ocean currents. Europe is influenced by warm ocean currents, such as the Gulf Stream, which transport heat from the tropics towards the region. These currents play a role in moderating temperatures and can contribute to the relatively higher warming observed in Europe. In contrast, Antarctica is surrounded by cold ocean currents, and its climate is heavily influenced by the Southern Ocean and the Antarctic Circumpolar Current, which act as barriers to the incursion of warmer waters, thereby limiting the warming effect.
Now, let's focus our analysis on Europe itself by examining temperature changes in different regions within Europe. We can achieve this by creating individual plots for each European region:
plot_temperature_changes
(["Southern Europe", "Eastern Europe", "Northern Europe", "Western Europe"])

From the plotted temperature changes in different regions of Europe, we observe that the overall temperature rises across the European continent are quite similar. While there may be slight variations in the steepness of the regression lines between regions, such as Eastern Europe having a slightly steeper line compared to Southern Europe, no significant differences can be observed among the regions.
Ten Countries Most and Less Affected by Climate Change
Now, let's shift our focus to identifying the top 10 countries that have experienced the highest average temperature increase since the year 2000. Here's an example of how we can retrieve the list of countries:
df[df.index.get_level_values(level="timestamp") >
date(2000, 1, 1)].groupby("area").mean().sort_values
(by="temp_change",ascending=False).head(10)
| area | temp_change | std_deviation |
Svalbard and Jan Mayen Islands | 2.61541 | 2.48572 |
Estonia | 1.69048 | nan |
Kuwait | 1.6825 | 1.12843 |
Belarus | 1.66113 | nan |
Finland | 1.65906 | 2.15634 |
Slovenia | 1.6555 | nan |
Russian Federation | 1.64507 | nan |
Bahrain | 1.64209 | 0.937431 |
Eastern Europe | 1.62868 | 0.970377 |
Austria | 1.62721 | 1.56392 |
To extract the top 10 countries with the highest average temperature increase since the year 2000, we perform the following steps:
- Filter the
dataframe to include only rows where the year is greater than or equal to 2000 using df.index.get_level_values(level='timestamp') >= date(2000, 1, 1). - Group the data by the '
Area' (country) using .groupby('area'). - Calculate the mean temperature change for each country using
.mean(). - Select the top 10 countries with the largest mean temperature change using
**.sort_values(by="temp_change",ascending=True).head(10)**.
This result aligns with our previous observations, confirming that Europe experienced the highest rise in temperature compared to other continents.
Continuing with our analysis, let's now explore the ten countries that are least affected by the rise in temperature. We can utilize the same method as before to extract this information. Here's an example of how we can retrieve the list of countries:
df[df.index.get_level_values(level="timestamp") > date(2000, 1, 1)].groupby
("area").mean().sort_values(by="temp_change",ascending=True).head(10)
| area | temp_change | std_deviation |
Pitcairn Islands | 0.157284 | 0.713095 |
Marshall Islands | 0.178335 | nan |
South Georgia and the South Sandwich Islands | 0.252101 | 1.11 |
Micronesia (Federated States of) | 0.291996 | nan |
Chile | 0.297607 | 0.534071 |
Wake Island | 0.306269 | nan |
Norfolk Island | 0.410659 | 0.594073 |
Argentina | 0.488159 | 0.91559 |
Zimbabwe | 0.493519 | 0.764067 |
Antarctica | 0.527987 | 1.55841 |
We observe that the majority of countries in this list are small, remote islands located in the southern hemisphere. This finding further supports our previous conclusions that southern continents, particularly Antarctica, are less affected by climate change compared to other regions.
Temperature Changes during Summer and Winter
Now, let's delve into more complex queries using the hierarchical dataframe. In this specific use case, our focus is on analyzing temperature changes during winters and summers. For the purpose of this analysis, we define winters as the months of December, January, and February, while summers encompass June, July, and August. By leveraging the power of pandas and the hierarchical dataframe, we can easily visualize the temperature changes during these seasons in Europe. Here's an example code snippet to accomplish that:
all_winters = df[df.index.get_level_values(level="timestamp").map
(lambda x: x.month in [12, 1, 2])]
all_summers = df[df.index.get_level_values(level="timestamp").map
(lambda x: x.month in [6, 7, 8])]
winters_europe = all_winters.xs("Europe", level="area").sort_index()
summers_europe = all_summers.xs("Europe", level="area").sort_index()
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(111)
ax.plot(winters_europe.index, winters_europe.temp_change,
label="Winters", marker="o", markersize=4)
ax.plot(summers_europe.index, summers_europe.temp_change,
label="Summers", marker='o', markersize=4)
ax.grid()
ax.legend()
ax.set_ylabel("Temperature Change [°C]")

From this figure, we can observe that temperature changes during the winters exhibit greater volatility compared to temperature changes during the summers. To quantify this difference, let's calculate the standard deviation of the temperature changes for both seasons:
pd.concat([winters_europe.std().rename("winters"),
summers_europe.std().rename("summers")], axis="columns")
| | winters | summers |
temp_change | 1.82008 | 0.696666 |
Conclusion
In conclusion, mastering MultiIndexes in Pandas provides a powerful tool for handling complex data analysis tasks. By leveraging MultiIndexes, users can efficiently organize and analyze multidimensional datasets in a flexible and intuitive manner. The ability to work with hierarchical structures for rows and columns enhances code clarity, simplifies data handling, and enables simultaneous analysis of multiple variables. Whether it's tracking health parameters of athletes or analyzing Earth's temperature changes over time, understanding and utilizing MultiIndexes in Pandas unlocks the full potential of the library for handling complex data scenarios.
You can find all code included in this post here: https://github.com/GlennViroux/pandas-multi-index-blog.
