BigDecimal in C#

• Download source code - 19.3 KB

Before Starting

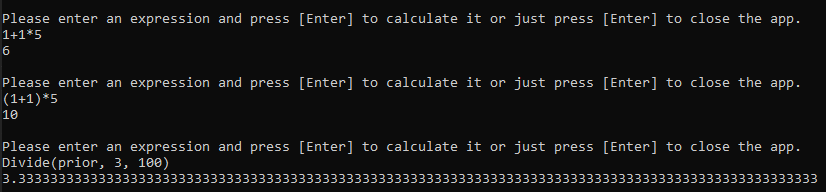
As you can see, the priority of the expressions, including the parentheses, is respected and, if we need, we can ask for 100 decimal places (even more if needed). Now, let's go to the actual article.

Introduction

C# (and .NET in general) right now don't come with a BigDecimal class. They only provide us with a BigInteger class.

It's funny that, to me, the only real difference between a BigInteger and a BigDecimal is the fact that the big decimal has a decimal separator (the dot, in American Standard) to divide integer numbers from the fractional/float numbers.

So, that's what I wanted to do: Have a class that stores any number as a BigInteger, and that also has another field (which I also made of a BigInteger) to tell where exactly the separator goes.

Maybe making the separator use a BigInteger is too much and an int or long will suffice, yet, I wanted to cover the maximum area possible.

How the Class Works

This is where the fun begins. When reading many articles on the internet, I saw that I need to divide things in 3 or more parts. I decided to start things simple: One integer number (that can be very big, that's why I used a BigInteger) and another number to tell where the dot (decimal separator) goes.

If the separator is at position 0 from end, that means the number is an integer number. If the separator is at the exact number of digits the number has, this means the number starts just after the "0." - that is 57 with a decimal separator at 2 from the end, becomes 0.57.

In fact, in my first implementation, I didn't allow the separator to go beyond the number of digits on the integer number, but that was not allowing me to generate numbers like 0.01. In this case, the integer number is 1, but the floating point position is 2, which is more digits than the number actually has (this is fixed/allowed now).

The Constructors

There are two main constructors for the class. One of them just receives a BigInteger. It assumes there is no floating point (or that it is at position 0 from the end) and calls the other constructor.

Then, there's a second constructor, which receives the full number as a BigInteger, and also a value telling where the decimal separator is, counting from the last position. So, it doesn't matter if the number is 123 or 1000... a 2 as the second argument means we will have two digits after the dot. So, 1.23 and 10.00 respectively... but, well... any zeroes at the left (before the decimal separator) or at the right, after the decimal separator, are eliminated, so the numbers will become, respectively, 1.23 and 10.

Maybe this isn't really necessary, but I started writing my code with an unsigned type... so, instead of storing positive and negative BigIntegers, I always store them as positive values, and just set a flag that the number is negative, if that's the case.

The First Operator... operator +

The first operator I decided to implement was the operator + (addition).

The first thought I had was: I need to make the numbers compatible.

The class stores just the integers, but with possible different values for where the dot separator appears. So, the values we see as 101 and 1.01 are both stored as 101, but one of them with the dot separator at 0, while the other with the dot separator at 2.

So, my solution was to get the separator with the greatest value (in this case, 2) and adapt all numbers to use that separator.

That means 101 with separator at 0 would become 10100 with separator at 2, while 101 with separator at 2 would remain exactly the same.

Now, it is just a matter of adding them up (10100 + 101 = 10201) and use the highest separator index, turning the number into 102.01.

The entire code looks like this:

public static BigDecimal operator + (BigDecimal a, BigDecimal b)
{
  var digitFromEnd0 = a._decimalIndexFromEnd;
  var digitFromEnd1 = b._decimalIndexFromEnd;

  var maxIndex = BigInteger.Max(digitFromEnd0, digitFromEnd1);
  var intA = _MakeItHaveThisAmountOfFloatDigits(a, maxIndex);
  var intB = _MakeItHaveThisAmountOfFloatDigits(b, maxIndex);

  if (a._isNegative)
    intA = -intA;

  if (b._isNegative)
    intB = -intB;

  var sum = intA + intB;
  return new BigDecimal(sum, maxIndex);
}

The method _MakeItHaveThisAmountOfFloatDigits will return the input number if the number of digits is the same, or will add some zeroes to the right until the right number of digits is reached.

It looks like this:

private static BigInteger _MakeItHaveThisAmountOfFloatDigits
(
  BigDecimal value,
  BigInteger numberOfFloatDigits
)
{
  if (value._decimalIndexFromEnd == numberOfFloatDigits)
    return value._value;  // Already right size. Do nothing.

  var diff = numberOfFloatDigits - value._decimalIndexFromEnd;
  var multiplier = new BigInteger(1);
  for (var i=0; i<diff; i++)
    multiplier *= 10;

  var intPart = value._value * multiplier;
  return intPart;
}

Other Operators

operator - (subtract)

The subtract operator is very similar to the add operator. I first make both numbers have the same number of digits... that is, the one with most digits to the right of the dot separator needs to be multiplied by 10 the right amount of times, then I do the subtraction.

When constructing a new number, as the constructor takes care of removing any trailing 0s on the right side of the dot separator, everything works fine.

Here is the entire code for the operator -:

public static BigDecimal operator - (BigDecimal a, BigDecimal b)
{
  var digitFromEnd0 = a._decimalIndexFromEnd;
  var digitFromEnd1 = b._decimalIndexFromEnd;

  var maxIndex = BigInteger.Max(digitFromEnd0, digitFromEnd1);
  var intA = _MakeItHaveThisAmountOfFloatDigits(a, maxIndex);
  var intB = _MakeItHaveThisAmountOfFloatDigits(b, maxIndex);

  if (a._isNegative)
    intA = -intA;

  if (b._isNegative)
    intB = -intB;

  var subtraction = intA - intB;
  return new BigDecimal(subtraction, maxIndex);
}

Multiplication (operator *)

I thought the multiplication would be a really tough one to implement... but it turns out it was simpler to implement than addition and subtraction.

I just multiply the integer representation of both values, and then I add the values of their "index from end" values of the dot/decimal separators. And I create a new value with that. That's all.

The code looks like this:

public static BigDecimal operator * (BigDecimal a, BigDecimal b)
{
  var digitFromEnd0 = a._decimalIndexFromEnd;
  var digitFromEnd1 = b._decimalIndexFromEnd;

  var intA = a._value;
  var intB = b._value;

  // It doesn't matter who is negative... as long as one is negative and the
  // other is not, we must make the result negative.
  bool isResultNegative = (a._isNegative != b._isNegative);
  var sum = a._value * b._value;
  if (isResultNegative)
    sum = -sum;

  var indexFromEnd = a._decimalIndexFromEnd + b._decimalIndexFromEnd;

  return new BigDecimal(sum, indexFromEnd);
}

Division (operator / and Divide Method)

Division is more complicated and I will not explain it here. By default, the operator / will call the Divide method passing 8 as the number of digits after the decimal separator.

You can, in theory, pass any number you want, but I noticed that after 1 thousand, the code becomes extremely slow... so, try not to go that far except if you really, really need to.

The example app uses 100 digits by default. It just does division of two numbers (that needs to use the . [dot] as decimal separator, you cannot use a different one independently of your computer region/settings) and you can see it supports really large numbers that fail with .NET provided decimal, numbers like 4328947293473294729347329847329432 for the divisor and 23423432432432432423423 for the divider will mess up with decimal, but BigDecimal will deal with those numbers with no issues.

What Else?

I implemented the method Power. I am still unsure if I should name it Pow and make it static, or if I keep it as Power and as an instance method. In fact, I am inclined to say that I want to make Divide become an instance method instead of keeping it as a static one.

In any case, I wrote many unit tests, and yet found some errors the tests didn't cover (so, then, I wrote some more tests to prove the issue... and then to prove the fix).

Consider the code still under development, but in particular for additions and subtractions, it should work quite well.

Different from BigInteger, this class will not limit the size of the string it will generate when calling ToString() so, if you use really big numbers, be aware that you might slow down or even crash your debugger by looking at the values stored in BigDecimals.

Well... that's all for now. If you want, download the sample and see if it works well for you. I hope it is useful for lots of people out there. And use the forum here to report any bugs you might find.

One Extra Detail

I made this class return 1 if you divide 0 by 0. This is to be compatible with the simplification done in formulas, where x/x is always one. If x is 0 and you don't do the simplification, 0/0 will throw in most cases. Well, in this class, it will match perfectly and will return 1. That's not a bug. That's really a trait of the class.

Conclusion?

You tell me. To me, it is already helping solve issues I had with decimals and the like when dealing with really large numbers where BigInteger was not appropriate.

BigRational

If you got the latest version of the download sample, you probably noticed that there's also a BigRational class. The idea of this class is very simple, but the implementation might not be as clear as it should be.

To avoid precision errors when we keep multiplying, dividing, then multiplying, then dividing (and so on), what the BigRational class does is that it keep multiplying the numerator when doing real multiplications and multiplying the denominator when we divide. It will only do a real division when we ask to convert the value of the BigRational to a BigDecimal.

That's the only moment that it might lose some precision, but assuming we might have done hundreds of multiplications and divisions before calling AsBigDecimal, we will have avoided hundreds of precision losses.

The Add and Subtract methods might be a little confusing, as they actually get their value multiplied by the denominator... that's what actually makes them work as expected, because they could only be added directly if we had already done the division (or when the denominator is 1).

Also, to avoid the values to just grow, all operations (Add, Subtract, Multiply and Divide) will call a method to "compress" the numbers. For example, if both the numerator and the denominator are even numbers, we can divide both by 2. This means both numbers get smaller, but the ratio they represent stays the same. So, don't be surprised if you store 100 and 50 but, in practice, the class stores 2 and 1.

Different from BigDecimal, this one is a class. I wanted to make it a struct but I needed the denominator to start with 1 and C# will naturally allow a "default" struct to be created (with zeros) and, instead of trying to deal with a denominator of 0, I decided to make the BigRational an actual class. If I get enough requests I might change my mind on that decision.

Well... I hope you enjoy both classes.

History

• 9^th August, 2023: Renamed some floatDecimalCount to floatDigitCount. In a Decimal class, all digits are expected to be decimals anyway. Also fixed Remainder/Mod test and comparison between positive and negative decimals;
• 8^th August, 2023: Added an updated version of MathParser to the sample app. So now users can write their own expressions instead of just dealing with divisions. The expressions support the basics like + - * / % and also a variable 'prior' to get the value from last execution as well as Divide and Power methods that allow setting the decimal precision;
• 7^th August, 2023: Implemented Power on my own, using BigInteger and with a binary/divide and conquer optimization;
• 5^th August, 2023: Renamed "nominator" to "numerator". Denominator stays the same;
• 5^th August, 2023: Added explanation of BigRational and made it support negative Power/exponent;
• 4^th August, 2023: Initial version.