Normals are unit vectors that are used widely for realtime 3D rendering but consist of 3 float (96bit) and often, there is no need to use high precision.
Introduction
While writing my C# code for a rendering tool using Directx library, I had the need to reduce the size of the normal vectors. I realized that the size of the data to be sent to the GPU and/or the file storage for a simple mesh geometry, increased excessively as the number of vertices increased.
The Normal is often used in 3D graphic to determine a surface's orientation, it consists of a 3xfloat vector with unit length so the values of x y z are in the [-1.0, 1.0] range.
Googling I found several methods but the one that seemed most effective to me is a spherical distribution of the vectors as described in this article:
I'll leave the article reading for any further information.
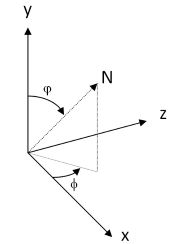
Polar Coordinates in Directx Coordinate System
Since the aim is to use the Directx library, it is necessary to define some basic math for left-handed coordinate system.
public struct Vector3f
{
public float x, y, z;
public float Normalize()
{
var length = (float)Math.Sqrt(x * x + y * y + z * z);
var l = length > float.Epsilon ? 1f / length : 0;
x *= l;
y *= l;
z *= l;
return length;
}
}
Convert a polar vector to unit vector and vice-versa. In the cartesian to spherical, we must consider that we work only with normal vectors and we must be sure that there are no divisions by zero.
public static Vector3f SphericalToCartesian(float r, float theta, float phi)
{
return new Vector3f(
r * Math.Cos(theta) * Math.Sin(phi),
r * Math.Cos(phi),
r * Math.Sin(theta) * Math.Sin(phi));
}
public static (float r, float theta, float phi) CartesianToSpherical(Vector3f cartesian)
{
float r = cartesian.Normalize();
float theta = (float)Math.Atan2(cartesian.z, cartesian.x);
float phi = (float)Math.Acos(cartesian.y);
return (r, theta, phi);
}
Unit Vector Quantization
To reduce the complexity, I decided to simplify the problem for positive Cartesian coordinates only, storing the sign of the normal in the first 3 bits (we are working in little endian).
ushort value = 0;
if (normal.x < 0) { value |= 1 << 15; normal.x *= -1; }
if (normal.y < 0) { value |= 1 << 14; normal.y *= -1; }
if (normal.z < 0) { value |= 1 << 13; normal.z *= -1; }
In this way, the phi and theta angles lies in [0, π/2] range. To quantize the angles, you can simply select a subdivision of your choice, for example, for N subdivisions, we would get:
d_phi = π/2 / N
d_theta = π/2 / N
so the angles can be represented by an index i and j where:
phi = d_phi * i
theta = d_theta * j
with i and j in [0,N] range
However, as written in the article, we will obtain a high density towards the Y pole. To improve the homogeneity of the distribution of the quantized vectors, I have chosen to vary the theta angle respect to phi. Considering that for phi=0, we have a division by zero, but any angle of theta is admissible, we will write:
float phi = i * d_phi;
float theta = i > 0 ? (j/i * π/2) : 0;
Now the problem is to store these two indices i and j in a 13-bit number, because 3-bit are reserved for the sign.
Table [i,j]
If we construct a table with rows i, columns j and a progressive number for this sequence:
int n = 0;
for (byte i = 0; i <= N; i++)
for (int j = 0; j <= i; j++)
i_tab[n++] = i;

We have a simple sequence, see also https://en.wikipedia.org/wiki/Triangular_number.
Using the formula n = (i+3)*i/2 ( or n=(i+1)*i/2+i ), we can calculate the maximum number of points on the quarter sphere used to quantize the normal vectors.
With N=126 subdivision for both i and j, the table generates 8128 points, and luckily with a 13bit number, we can encode a number from 0 to 8191.
Encoding
static int sum(int i) => (i + 1) * i / 2;
public static ushort Encode(Vector3f normal)
{
ushort value = 0;
if (normal.x < 0) { value |= 1 << 15; normal.x *= -1; }
if (normal.y < 0) { value |= 1 << 14; normal.y *= -1; }
if (normal.z < 0) { value |= 1 << 13; normal.z *= -1; }
Mathelp.CartesianToSpherical(normal, out _, out float theta, out float phi);
int i = (int)Math.Round(phi / d_phi);
int j = (int)Math.Round(theta * i * 2 / PI);
int n = sum(i) + j;
#if DEBUG
if (n > MAX || n < 0) throw new Exception("Fail");
#endif
value |= (ushort)n;
return value;
}
Decoding
To reverse the calculation, we first need to get the i and j indices back from the 13bit value. We can use two methods:
- Using the precalculated table but require to store a byte[8128] table:
int i = i_tab[value];
int j = value - sum(i);
- Using the
inverse function. These formulas can be used for example in a HLSL Shader code. Currently, the sqrt function doesn't impact performance at all (comparing to older graphics architectures). However, they must be checked for each value because it is possible that the precision of the floats can give different values.
static void inverse(int n, out int i, out int j)
{
i = (int)(Math.Sqrt(1 + 8 * n) - 1) / 2;
j = n - sum(i);
}
static void inverse_aprox1(int n, out int i, out int j)
{
i = (int)(Math.Sqrt(n) * rad2);
j = n - sum(i);
if (j < 0) { j += i; i--; }
}
static void inverse_aprox2(int n, out int i, out int j)
{
i = (int)(Math.Exp(0.5 * Math.Log(n)) * rad2);
j = n - sum(i);
if (j < 0) { j += i; i--; }
}
HLSL shader code
tested with directx11, but I don't know now to measure the performance
float3 DecodeUnitVector16(min16uint encode)
{
int n = encode & 0x1FFF;
int i = (sqrt(1 + 8 * n) - 1) / 2;
int j = n - (i + 1) * i / 2;
float phi = i * 1.5707963267 / 126;
float theta = i > 0 ? j * 1.5707963267 / i : 0;
float3 normal = float3(cos(theta) * sin(phi),cos(phi),sin(theta) * sin(phi));
if ((encode & 0x8000) != 0) normal.x *= -1;
if ((encode & 0x4000) != 0) normal.y *= -1;
if ((encode & 0x2000) != 0) normal.z *= -1;
return normal;
}
Result
If we create all possible values with this code, we obtain a dense and homogeneous distribution of unit vectors, for a total of 65.024 possible points, as shown in the image.
for (int sign = 0; sign < 8; sign++)
for (int n = 0; n <= 8127; n++)
{
int code = n | sign << 13;
Vertices.Add(Decode((ushort)code));
}
Any comments or suggestions to improve the code are welcome.

Extension to 24bit
In the source code, I added the 24bit extension, which N=2046 generates 2.096.128 points for one quarter of sphere, so a total of 16.769.024 possible normals.
The extension to 32bit doesn't make sense also because I encounter memory overflow errors.
Performance
The bottleneck is due to the trigonometric functions. A doubling of the speed is obtained by replacing the standard functions with approximations (which are under testing):
static float Sin(float r)
{
float n = (Mathelp.PI - r)*r * 4;
return n * 4 / (5 * Mathelp.PI * Mathelp.PI - n);
}
static float Cos(float r)
{
return (Mathelp.PI2 - 4 * r * r) / (Mathelp.PI2 + r * r);
}
static float AcosTR(float x)
{
return (float)(8 / 3.0 * Math.Sqrt(2 - Math.Sqrt(2 + 2 * x)) - 1 / 3.0 *
Math.Sqrt(2 - 2 * x));
}
static float AcosSL(float x)
{
var z = Math.Abs(x);
z = (float)((-0.168577f * z + 1.56723f) * Math.Sqrt(1 - z));
return x < 0 ? z + Mathelp.PI : -z;
}
History
- 22nd August, 2023: Initial version
