We'll be doing a deep dive from concepts to implementation in terms of how finite automata works, with help from my Visual FA solution.
Introduction
This is yet another attempt at Visual FA. My first attempt suffered from performance problems that were hidden by flaws in the benchmark code. To fix the issue required a total rewrite, everything from the runtime logic to the generator and compiler. Let's take a moment to feel sorry for me. =) Or shame me, as is your preference. Whatever works.
In any case, there is a lot of ground to cover so I'm breaking this into a multipart series and starting from the beginning, even if it means we're covering territory in previous articles.
We'll be using Visual FA to do everything here, so all of the article's content is with an eye toward this engine. When comparing other engines, such as Microsoft's that will be noted.
Article list
Prerequisites
- You'll need a recent copy of Visual Studio.
- You'll need Graphviz installed and in your PATH.
- You'll need to accept the fact that there are a couple of executables included in the root folder of this project that are necessary for building - deslang.exe and csbrick.exe - hit the search box in CodeProject - there's articles for each here, and there's code on github too, for both - see the README.md in this solution for links to them. They're harmless and necessary. This project can't do half the neat stuff it does without some fancy footwork during the build.
What is Visual FA?
In short, Visual FA is basically a regex engine. That's simplifying it a lot and it will probably just lead to more questions. The long answer is it is a finite automata simulator, code generator and compiler for matching patterns in Unicode streams.
Microsoft Already Provides Regex! What Gives?
True, Microsoft offers a snazzy backtracking engine that can compile and generate code. What it can't do is tokenize text, at least not without some serious compromises, hacks, and performance penalties. It also trades away speed for features. What sets Visual FA apart is that it is a minimalist engine with no backtracking, anchors, or any other fluff that may get in the way of raw performance, plus it has lexing/tokenizing capabilities.
So primarily, if you need to lex/tokenize, you'll need to use an engine other than Microsoft's. Visual FA fits the bill. Secondarily, if you don't need fancy features, and you want a bit more performance, this library is also a viable candidate, being up to 3 times faster in some cases.
And finally, Microsoft's engine can't show you all of its guts, and generate pretty graphs. All of the images in this article were generated using Visual FA, with the help of Graphviz.
This article is primarily an exploration of concepts peppered with a quick start guide on using Visual FA to do fundamental operations.
Regex Crash Course
You don't need to be a regex expert to enjoy this article, but having some fundamentals down is really helpful. Visual FA's syntax is minimalist and relatively simple. Furthermore, we won't cover everything Visual FA supports here, because it's not entirely necessary.
Regular Operators:
- Concatenation (implicit):
ABC - matches "ABC" - Alternation
|: ABC|DEF - matches either "ABC" or "DEF" - Character set:
[A-C] - matches either "A", "B" or "C" - Not character set:
[^A-C] - matches any character other than "A", "B" or "C" - Optional
?: A? - matches either "A" or "" - Repeat zero or more
*: A* matches "A" or "" or "AAAAAAAA" - Repeat one or more
+: A+ matches "A" or "AAAAAAAA" - Repeat([min],[max])
{,}: A{2,} matches "AA" or "AAA" or "AAAAAAA" () - precedence overriding (aka (?:) ): (ABC)? - Matches "ABC". Note that Visual FA does not sub-capture.
With Visual FA, you can parse an expression into an Abstract Syntax Tree (AST) or directly into a state machine:
using VisualFA;
FA fa = FA.Parse("foo|bar");
RegexExpression exp = RegexExpression.Parse("foo|bar");
fa = exp.ToFA();
Understanding Finite Automata
Actually, that's a bit of an overstatement of scope - we'll be looking at two specific kinds of finite automata used for matching patterns in a flat stream (series of elements, but no hierarchies of elements): NFAs and DFAs.
These stand for Non-deterministic Finite Automata and Deterministic Finite Automata respectively, and they are two kinds of finite state machine.
A Confusing Rabbit Hole of Terms
The terminology is playing a little loose there, as these two types are more specific types of state machines than their names would otherwise imply. All finite automata machines - that is, all state machines are either deterministic or non-deterministic, even including push down automata and other types of state machines we won't be exploring here. That said, when you see NFA and DFA in the mathematical sense, you can usually assume we mean the two types of machines we'll be covering here.
If instead, you see NFA and DFA being used to describe a category of regular expression engine, that's a little bit different, although just to be difficult, they come from the same origins. Visual FA can handily deal with NFA state machines, but its regular expression engine is strictly the DFA type. Microsoft's Regex engine is by contrast, an NFA type. DFA regular expression engines typically build NFA machines out of expressions and then transform those into DFA machines to do the actual matching. Visual FA is no exception. It does however, complicate things because it can run a match using an NFA machine without first converting it to a DFA. Even in this case though, it is essentially acting on that machine as though it will be turned into a DFA. Microsoft's engine by contrast, has things on their NFA states that cannot be transformed into a DFA. Visual FA does not. In effect, Visual FA's NFAs are just future DFAs in waiting. If you don't understand all of this yet that's fine, but maybe revisit it later if you start to question the terminology used as you read further.
Some Basics - Finding One's Way Around
The set of all states reachable from a state directly or indirectly via transitions - including itself, is known as the closure of a state.
This is important because in Visual FA, your "handle" for the entire state machine is always the root state (known as q0 canonically but you can call it what you like). The closure of q0 is always the entire machine. Review this material after you look through the very next section, because it has pretty pictures, and they really help here.
Essentially, you can build or parse a state machine into existence, and what you get from one of those builder or parse functions is the root of what it built:
FA myMachine = FA.Parse("foo|bar");
Here, myMachine is actually q0, which we'll see below, under the very next section.
myMachine has a total of 6 states, including itself.
List<FA> closure = new List<FA>();
myMachine.FillClosure(closure);
Console.WriteLine("myMachine has {0} states.",myMachine.Count);
Debug.Assert(myMachine==closure[0]);
That's kind of longhand way to perform a closure. There's a shorter way to call it:
IList<FA> closure = myMachine.FillClosure();
The first form allows you to recycle list instances which is important for doing set heavy operations. That's why Visual FA uses FillXXXX() methods instead of always returning new lists. FillClosure() is expected to be called frequently, so it is orchestrated accordingly.
Understanding How DFAs Work
We'll start with DFAs since they are the simplest type of machine to understand. All finite state machines are directed graphs of states with transitions to other states on particular inputs:
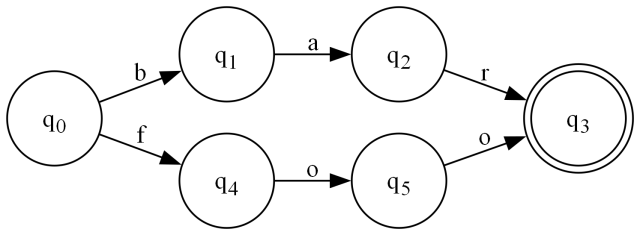
This is a DFA state machine matching the text "foo" or the text "bar" (foo|bar).
- We always start at q0.
- We can only move in the direction indicated by the arrows.
- On each state q, we examine the current codepoint* under the cursor, and the list of outgoing arrows. If there is an arrow with the input codepoint on it, we must follow that arrow and advance the cursor by moving to the next codepoint.
- If there are no matching outgoing transitions from 3, then we must evaluate the current state that we're on now. If it's a double circled state, that means we can return the input we've gathered so far as a match. If it's not a double circled state, then there was no match.
* codepoint indicates the UTF-32 Unicode codepoint under the cursor that we're examining. For most situations, this is effectively your current character. The exception is in the case of UTF-16 surrogate characters, which will be resolved to a single UTF-32 codepoint for evaluation in the machine. We don't deal with surrogates at this level, so there's nothing to complicate it.
You can use the FSM Explorer application included with this solution to produce and visually step through a regular expression with some input text.
Enter the NFAs
Typically, every DFA starts out life as an NFA*. The reason is that NFAs are far easier to construct programmatically through parsing or composition of several machines (we'll cover that). We don't keep them as NFAs because NFA graphs are more complicated than DFA graphs for a computer to traverse.
* The latest bits at GitHub will produce DFAs from simple expressions directly from the parse. This isn't always true, but it will when it doesn't have to do anything to transform the state machine. You can determine if an entire machine is deterministic by using the IsDfa() method.
The primary difference between an NFA and a DFA is that an NFA adds the ability to be in more than one state at once.
This can happen in one of two ways:
- There exists more than one outgoing arrow from a state with the same codepoint but branching to different destination states. This is the case with a "compact" NFA, which we'll cover.
- There is the presence of an epsilon transition. These are unlabeled arrows that can be moved on without advancing the input. Every epsilon transition must be followed as soon as it is encountered but it does not transition you away from your current state, leading to situations where you can be in more than one state. This is the case with the "expanded" NFA machines.
Here is effectively the same machine as the above, but represented as an expanded NFA.

The gray dashed arrows are epsilon transitions as explained in #2 from the above list. Note that you always follow every epsilon transition you encounter immediately. That means as soon as you are in q0, you are also in q1 and q6 as well.
Here are the rules for walking NFAs. They are nearly the same as the DFA rules, just accounting for epsilon transitions and multiple states:
- We always start at q0
- For each state we are in, we always immediately follow every epsilon and add its destination to the list of states we're currently in. Another way to put this is we take the epsilon closure of our current states. (The set of all states reachable from some states along only epsilon transitions is called the epsilon closure.)
- We can only move in the direction indicated by the arrows.
- For each current state in our set of current states, we examine the current codepoint* under the cursor, and the list of outgoing arrows. If there is an arrow with the input codepoint on it, we must follow each matching arrow (there may be more than one) and advance the cursor by moving to the next codepoint.
- If there are no matching outgoing transitions from 3, then we must drop that state from our next states list.
- If we have no possible next states from our current states, then we evaluate the current states that we're in now. If any are double circled states, that means we can return the input we've gathered so far as a match. If none are double circled states, then there was no match.
A state in a state machine is represented by the VisualFA.FA instance, regardless of whether the machine is a DFA or an NFA.
Let's revisit this machine in code:

using VisualFA;
FA q0 = FA.Parse("foo|bar",0,false);
IList<FA> closure = q0.FillClosure();
IList<FA> epsilonClosure = FA.FillEpsilonClosure(new FA[] { q0 });
Composing NFA Machines using Thompson's Construction Algorithm
Thompson's construction algorithm is a well known (among FA nerds, that is) algorithm for converting regular expression operators into NFAs. The idea is that each operation has a well known construction for building it, and then you compose those together like Legos to build your final expression.
Let's start with arguably, the simplest - a literal - ABC: (This is technically 3 literals concatenated in regex parlance, but it's nice for reasons to treat a literal string as a first class entity.)

FA ABC = FA.Literal("ABC");
And for our second more or less "atomic" construct, a set [ABC]:

FA AthroughC = FA.Set(new FARange[] {new FARange('A','C')});
Now for simple concatenation, ABC(DEF):

FA ABC = FA.Literal("ABC");
FA DEF = FA.Literal("DEF");
FA ABC_DEF = FA.Concat(new FA[] { ABC, DEF });
Next, a little alternation ABC|DEF:

FA ABC = FA.Literal("ABC");
FA DEF = FA.Literal("DEF");
FA ABCorDEF = FA.Or(new FA[] { ABC, DEF });
Next, an optional match (ABC)?:

FA ABC = FA.Literal("ABC");
FA ABCopt = FA.Optional(ABC);
Finally some repetition/looping: (ABC)+:

FA ABC = FA.Literal("ABC");
FA ABCloop = FA.Repeat(ABC,1,0);
We can compose everything by treating every expression as its own machine, and then composing those machines together. The above graphs are fundamental machines that all other machines can be built out of. Such is the advantage of using NFAs at this stage. DFAs cannot be readily composed.
Speaking of which:
From NFA to DFA - The Power of Powerset Construction
Powerset construction, or subset construction depending on who you ask is basically the process of creating a new DFA that matches the same input as a given NFA. It has been proven mathematically that this is possible for any NFA that follows the rules in this article. The trick is finding it. The primary idea is each and every combination of states you can possibly be in in an NFA represents a single state in the new DFA, with its transitions merged into that single state.
This doesn't always work, because with an NFA, you can transition to more than one state on any given input. What the powerset construction does to account for that, is bubble the conflict further down the path - such that it tries to disambiguate further down the line.
Here's a pair of figures that we'll go over. This is a machine that determines whether the input is a line comment or the beginning of a block comment:

The top machine is an NFA in compact form. The bottom machine is the equivalent DFA (not minimized - q4 could potentially be eliminated and rolled into q3).
The bottom graph has { } sets below each state label. These sets are the set of states from the NFA that yielded the state in the DFA. For example, q0 in the DFA was simply q0 in the NFA. However, transitioning from q0 on / in the NFA brings us to two different states, q1 and q3 both. q1 in our DFA reflects that.
Notice how the DFA transformation bubbled the disjunction/divergence on / further down the path, from q0 to q1 in the DFA on * vs. / instead. That's what I was trying to get at earlier about dealing with ambiguities. The construction algorithm assumes that if you traverse far enough eventually, there will be some kind of differentiating input. When that's not the case, one expression blindly pushes the other aside and effectively shadows it.
FA nfa = FA.Parse(@"(\/\/[^\r\n]*)|(\/\*)");
FA dfa = nfa.ToDfa();
FA min_dfa = nfa.ToMinimizedDfa();
Wait, What the Heck is Lexing?
I've mentioned lexing and tokenization more than once. To tokenize a document means to take the text therein and break it into a series of tokens, each token representing a position, the value that was matched, and a symbolic matched expression (or an error symbol if no expression was matched). This is often used by parsers to parse structured text.
Since Microsoft's parser can't do this, you may not be familiar with that usage for regular expressions, but it is as bread and butter for regex as matching text in strings is.
In order to work, your state machine needs to be composed of multiple expressions. Each expression has an associated symbol it is tagged with. Visual FA calls this the accept symbol. As you retrieve matches over inputs, a match is reported with the associated accept symbol for the expression that matched the text at the reported position. Every portion of the document is returned, including sections that weren't matched. They will be reported with an accept symbol of -1.
All of this engine's searching facilities report all of the text - even unmatched portions. That makes it significantly different than Microsoft's offering, and usable in more scenarios. If you want it to work like Microsoft's, you simply need to ignore FAMatch instances whose IsSuccess property is false or whose SymbolId property is less than zero.
Here's an example of what a lexer might look like (presented in DFA form):

Note the special dashed transition outgoing from q10. This is not an epsilon transition - those are gray and have no label on them - this is a lazy match simulation transition to a "block end". We'll cover block ends and the need for them next.
"Block Ends" - A Relatively Simple Solution to a Sticky Problem
DFA machines cannot lazy match. Well, there is one person that claims to have figured it out, and has provided an implementation, but I fear it explodes the state table size if I understand it properly, and I'm not sure that I do. In any case, DFA machines always consume input until they have nowhere left they can move, even if a shorter string would have yielded a valid match. This is called greedy matching.
Sometimes it's not what you need. In particular, those times tend to be cases where you need to match multicharacter ending conditions to arbitrary text, like finding the end of HTML/SGML/XML comments and CDATA sections, or finding the end of C style block /* */ comments as we've done. To do so requires lazy matching. It requires telling the engine to stop being so greedy! However, we cannot communicate that to the engine without breaking the math of the NFA to DFA transformation.
Here's what we do instead: As alluded to before, each expression has a non-negative integer accept symbol associated with it.
Each accept symbol meanwhile potentially has another expression/state machine associated with it known as a "block end". If it has one, then when the initial expression is matched, the matcher will keep consuming input up until and including the point where the block end expression is matched.
Despite only allowing one per expression, and only allowing for accepting any and all characters through the final match, this still covers probably 80% of the use case for lazy matching without requiring a fundamental change in how any of the mechanics of the engine work.
With Visual FA, you specify your block ends at the time of execution for the runtime engine, at compile time when using the compiled matchers, and at generation time when using generated matchers. They are always specified as an array where the index into the array corresponds to the accept symbol associated with that block end. The array can be null, and does not need to be the entire size necessary to hold the maximum accept symbol - only the maximum accept symbol with a block end attached to it.
FA commentBlock = FA.Parse(@"\/\*", 0);
FA commentBlockEnd = FA.Parse(@"\*\/");
foreach(FAMatch match in commentBlock.Run("foo /*bar*/ baz",
new FA[] { commentBlockEnd}))
{
Console.WriteLine("{0}:{1} at {2}",
match.SymbolId,
match.Value,
match.Position);
}
This will print the following to the console:
-1:foo at 0
0:/*bar*/ at 4
-1: baz at 11
As mentioned, the runners will always return the entire text. If you only want the bits that matched, check each FAMatch instance for IsSuccess.
How a DFA Executes
Let's walk through the execution of a DFA as though it was C# code:
int cp;
int len;
int p;
int l;
int c;
cp = -1;
len = 0;
if ((this.position == -1)) {
this.position = 0;
}
p = this.position;
l = this.line;
c = this.column;
this.Advance(s, ref cp, ref len, true);
q0:
if ((cp == 47)) {
this.Advance(s, ref cp, ref len, false);
goto q1;
}
goto errorout;
q1:
if ((cp == 42)) {
this.Advance(s, ref cp, ref len, false);
goto q2;
}
goto errorout;
q2:
return _BlockEnd0(s, cp, len, p, l, c);
errorout:
if (((cp == -1)
|| (cp == 47))) {
if ((len == 0)) {
return FAMatch.Create(-2, null, 0, 0, 0);
}
return FAMatch.Create(-1,
s.Slice(p, len).ToString(),
p,
l,
c);
}
this.Advance(s, ref cp, ref len, false);
goto errorout;
The basic idea is to always have a current input you're looking at. This might require a corner case on the first input depending on what your source input API looks like. Once you do:
- Store the current location
- For each state in the machine
- Check the transitions for any match
- When matched, capture the current input and advance the cursor, plus jump to the next state
- If not accepting, error
- If accepting, either return the current match, or proceed to the associated block end function if there is one.
- On error, we look to see if the current input matches anything from q0. If not, we capture it. If so, we return what we have so far as an error "match". If we didn't match anything, and we haven't captured anything, report an actual end of input.
In the block end, things are slightly simpler:
q0:
if ((cp == 42)) {
this.Advance(s, ref cp, ref len, false);
goto q1;
}
goto errorout;
q1:
if ((cp == 47)) {
this.Advance(s, ref cp, ref len, false);
goto q2;
}
goto errorout;
q2:
return FAMatch.Create(0,
s.Slice(position, len).ToString(),
position,
line,
column);
errorout:
if ((cp == -1)) {
return FAMatch.Create(-1,
s.Slice(position, len).ToString(),
position,
line,
column);
}
this.Advance(s, ref cp, ref len, false);
goto q0;
What's Next?
Next, we will cover the API mechanics in more detail, as well as how that works, followed by compilation and code generation. You can find it here.
Enjoy.
History
- 15th January, 2024 - Initial submission
