A discussion about recursive algorithms in general that concentrates on the Minimax algorithm in particular and its application in a game of Tic Tac Toe.
Introduction
The concept of recursion, where a method calls another instance of itself, can be somewhat difficult to understand because it requires, to some extent, 3D thinking. There is a need to consider both the input and output parameters and the depth of the recursive calls. So it may be helpful to consider a simple example before delving into the more complex Minimax algorithm
Recursive Algorithms
Recursive algorithms are functions that call another instance of the same function within itself. They all have certain characteristics in common that are best shown by a simple example. Here’s a recursive method that calculates x raised to the power of n
public int XPowerN( int x, int n)
{
if (n==0 )
{
return 1;
}
int nMinusOneResult=XPowerN( x, n-1 );
return nMinusOneResult * x;
}
The method has to be able to output a result that’s generated internally without making a recursive call, otherwise a coding black hole will be created from which there is no return. In this case the method escapes from itself when n=0 and it returns a value of 1. For other values of n the method depends upon the work done incrementally by other calls to the same method. In this example the method needs the result from a recursive call with n-1 as a parameter, then it simply multiplies x by the value returned. A call with n=4 will involve 4 recursions; the 4 calls are stored on the stack and form a first in last out queue. So the first method call to complete is when n=o. The final result is built up incrementally as each call to the method completes. It’s this incremental approach that tends to cause problems so it's important to maintain a good degree of separation between the parent method and any child recursive calls. Creating new instances of reference types before using them as parameters is preferable to giving every call the same object instances and hoping that they don't get too mangled in the process.
Minimax
Minimax is a recursive algorithm that’s often used in game play to select the best move that a player can make. It does this by building a move look-ahead tree where every relevant move and subsequent move is explored over multiple plays, then it returns the best move found. There is an optimisation named Alpha-beta pruning that’s used to prevent moves from being explored that cannot possibly return a better result than a move that has already been discovered. The game used here as an example is Tic-Tac-Toe its board is a 3x3 matrix of squares and each move by one of two players results in one square being occupied by that player’s marker. One player uses X as a marker and the other an O. The winner is the first to put 3 of their marks in a single row, column or diagonal. The result is always a draw if both players play optimally. Here is a diagram showing the path that the algorithm takes when building and traversing the look-ahead tree. The game in this example starts from when there are only 3 moves left to play and it’s Max’s (X) turn to move. The scoring system is very simple, Max scores +1 for a win and Min, the other opponent, scores -1 for a win. A draw scores zero. The path that the algorithm takes can be traced by following the arrows from left to right.
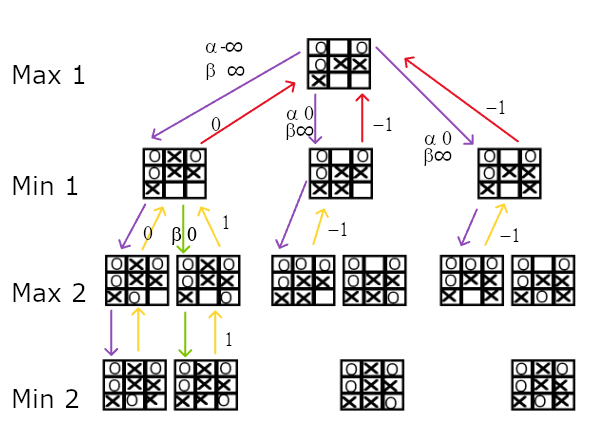
The Parent/Child Relationship.
The root node has three child nodes at the Min1 level, one for each of the move options that Max has. The child nodes are themselves parents of nodes that explore all the moves that Min can make in response. This parent/child relationship continues until there is a winner or there are no more moves left to explore.
The Variables Used By Minimax.
Two variables, alpha and beta, are passed down from parent to child on each recursive call. Alpha keeps a record of the best score found by Max in the search and beta does the same thing for Min. Only Max can update alpha and only Min can update beta. The score is passed up from child to parent as the value that’s returned from the call to Minimax. Max nodes always return the highest score found and Min nodes always return the smallest, in other words both players make their best move and gambits are forbiden. The way data is passed and updated between parent and child nodes is the key to understanding how the algorithm works.
Evaluation Of The First Child Node.

The first child of the root node explores all the move possibilities that result from Max placing an X at zero-based index 1. Its 2 child nodes in turn consider the option of placing an O at index 7 and at index 8. At level Min2 the recursion ends and returns a score of 0 to its parent. Its parent at Max2 has no further child nodes so that recursive call ends and returns 0 to its parent at Min1. The best score seen by the node at Min1 is now 0 and beta is updated to that value having previously been the default value of positive infinity. For Min the lower the score the better. The node keeps a record of the lowest score returned from its children as that’s the value that the node returns when the method call completes. It also checks to see if its parent node, the root, has already had a better score returned to it. The best score that the root has seen is the alpha value, it has not been updated from the default value of negative infinity so there is no better choice for Max to choose and it’s worth exploring the second child node to see if it returns a better (lower) value for the Min node. In the event it returns a higher score (+1) so the Min node returns its best score (0) to the root node and that node updates its alpha value to 0. There is some economy of effort here as the tree is built and evaluated at the same time
Alpha Beta Pruning.

Alpha Beta pruning occurs with the second and third child nodes of the root. The root's alpha setting has been updated to zero as a result of the 0 being returned from the first child node. The second and third child nodes of the root both receive -1 from their own first child. This updates beta to -1, it was previously set to positive infinity. Beta is now smaller than alpha. The root has already found a zero option and the best result that can be returned for Max from continuing to explore these two nodes is -1. They would return an even lower value if one was found as Min nodes always return their lowest value. So the recursions end and -1 is returned to the root. These two pathways are pruned because Max is never going to travel down them. Notice that the root’s beta value is not updated as it does not have a parent Min node. It is only Min nodes that can change beta and pass it down to its children.
The Minimax Algorithm.
The code shown below could be refactored but, hopefully, in its present form it is relatively easy to follow. An IEnumerable<int> is used as a parameter representing the board rather than an array so that, if changes need to be made, a new array instance needs to be created and the opportunity for multiple iterations of the method to work on the same array instance is reduced. Numeric values of x=1 O=-1 and Space=0 are used rather than character symbols as Minimax is more concerned with calculating values than displaying them. For example a matched line has a total value of +3 or -3. The depth parameter is used to limit the depth of the move search to give opponents a better chance of winning.
public int Minimax(IEnumerable<int> board,
int depth,
int alpha,
int beta,
bool isMaxingPlayer)
{
if (lineService.CheckForAWin(board, !isMaxingPlayer))
{
int eval = isMaxingPlayer ? -1 : 1;
return eval;
}
if (depth == 0)
{
return 0;
}
if (isMaxingPlayer)
{
int maxScore = int.MinValue;
foreach (var childBoard in lineService.GetChildBoards(board, isMaxingPlayer))
{
int score = Minimax(childBoard, depth - 1, alpha, beta, false);
if (score > maxScore)
{
maxScore = score;
}
alpha = score > alpha ? score : alpha;
if (beta <= alpha)
{
break;
}
}
return maxScore;
}
int minScore = int.MaxValue;
foreach (var childBoard in lineService.GetChildBoards(board, isMaxingPlayer))
{
int score = Minimax(childBoard, depth - 1, alpha, beta, true);
if (score < minScore)
{
minScore = score;
}
beta = score < beta ? score : beta;
if (beta <= alpha)
{
break;
}
}
return minScore;
}
Unit Testing Minimax
There is a gotcha, an unexpected expected value, when testing the algorithm. The algorithm is unbeatable but it doesn’t always find the fastest way to win. In the following situation where the game is lost for Min it selects the square at index 4 instead of the quick win at index 6. This is because the evaluation of the first child Min node has an X at index 4 and it returns the best possible (+1) score for Max as every option open to Min results in a win for Max. So Index 4 is returned as Minimax outputs the first best option found.

The Eample Application
The example application is very simple. It outputs the result, a slow draw, where Minimax plays for both sides then a quick win when Minimax plays X against a random O. There is also an asynchronous example where progress is reported as Minimax plays random 0 over 500 games. Spoiler alert! O never wins and there are less than 5 draws.
public async Task<(int xCount, int oCount)> LookForAWinner(int gamesToPlay)
{
var progressHandler = new Progress<string>(Console.WriteLine);
int totalGames = gamesToPlay;
int winnerCountX = 0;
int winnerCountO = 0;
for (int g = 1; g <= totalGames; g++)
{
int[] board = new int[9];
bool isMaxingPlayer = true;
for (int i = 0; i < 9; i++)
{
int moveIndex = isMaxingPlayer ? await GetBestMove(board, 0, isMaxingPlayer)
: lineService.GetRandomMove(board);
int symbol = isMaxingPlayer ? 1 : -1;
board[moveIndex] = symbol;
if (lineService.CheckForAWin(board, isMaxingPlayer))
{
winnerCountX = isMaxingPlayer ? winnerCountX + 1 : winnerCountX;
winnerCountO = isMaxingPlayer ? winnerCountO : winnerCountO + 1;
break;
}
isMaxingPlayer = !isMaxingPlayer;
}
if (g % 50 == 0 && progressHandler is IProgress<string> progress)
{
string report=$"Games played {g} Winners found Player X= {winnerCountX} Player O = {winnerCountO}"
progress.Report(report);
}
}
return (winnerCountX, winnerCountO);
}
Conclusion.
The Minimax algorithm is very useful in implementing a game play strategy but some caution is needed with the variables used and the number of recursive calls made in order to avoid spurious results and the dreaded stack overflow exception.
