Introduction
Though the title is from the famous story by O. Henry, this article has nothing to do with the plot of that story and can be also titled:
Along the Lines and Between the Walls
The examples for this article can be divided into two separate groups but because they use the same programming technique I decided
to unite them under one title. These examples are similar to some examples from the book World of Movable Objects and I would say that the set of
examples in the book has more details. Also I have to admit that there is more logic in the explanation in the book which you can find at http://sourceforge.net/projects/movegraph/files/?source=directory.
In addition to the book and the huge demo program with all its codes you can
find there an additional document with descriptions of all the methods from MoveGraphLibrary.dll. This library is needed to start the accompanying application. If you see in the text below any mention of source files
which are not included in the project accompanying this article, then these are the files from the project accompanying the book.
Let’s start with some general rules for all the further examples.
- Everything is movable. To move an
object, you simply press it with the left button and move it to any location
you want. The movement is over when you release the button.
- Parameters of visualization can be
changed at any moment. To change the view of an object, you have to call a
context menu on this object and select the needed command.
Any movement of each and all objects are organized
with only three mouse events: MouseDown, MouseMove, and
MouseUp. Movements are supervised by a special object of the Mover class and the method for each of these three events
contains only one call to one or another method from the Mover class. Everything is pretty easy and is explained at
the very beginning of the mentioned book World of Movable Objects.
Often enough movements have some restrictions; for
example, there can be a limitation on the size of a particular object or an
object is allowed to move only inside some area. In general, when there is
some limitation on the movement, then an object can be stopped while the mouse
(the cursor) continues to move. In the examples of this article there is some
difference in this particular situation: when an object has to stop because of
some restrictions, then the mouse cursor also stops and stays at the same spot
of an object. It looks like the cursor is adhered to the spot where an object
was originally pressed with a mouse.
The first part of examples deals with the movements of
objects along predefined tracks; these tracks can be shown or hidden from
view, but for the algorithm it doesn’t matter at all. Let us start with the
preliminary example of moving a simple object – a small colored spot – along
the segment of a straight line or along an arc.
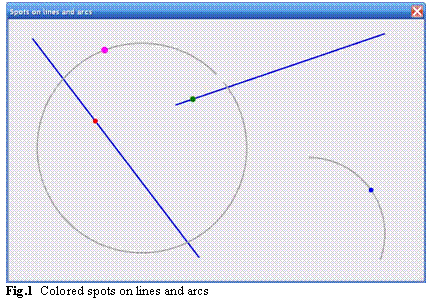
- File: Form_SpotsOnLinesAndArcs.cs
- Menu position: Spots on lines – Spots on lines and arcs
There are two straight lines and two arcs in Form_SpotsOnLinesAndArcs.cs (figure 1). There is a small colored spot on each of these lines
(straight or curved) and each spot can move only along its trail and only between the ends of this trail. Usually it is easier to deal with the straight
lines, so let us start with the SpotOnLineSegment class.
public class SpotOnLineSegment : GraphicalObject
{
Form form;
Mover supervisor;
PointF m_center;
int m_radius;
SolidBrush brush;
PointF ptEndA, ptEndB;
float dxMouseFromCenter, dyMouseFromCenter;
An object of the SpotOnLineSegment class is characterized by the position of its central
point (m_center), radius (m_radius), and
the brush (brush) with which it is painted. Such a colored spot is
allowed to move only along the straight segment, so the end points of this
segment must be declared (ptEndA and ptEndB). The
central point of the colored spot is placed exactly on the declared segment with
the help of the Auxi_Geometry.NearestPointOnSegment() method.
public SpotOnLineSegment (Form frm, Mover mvr, PointF pt0, PointF pt1,
PointF pt, int r, SolidBrush brsh)
{
form = frm;
supervisor = mvr;
ptEndA = pt0;
if (Auxi_Geometry .Distance (pt0, pt1) >= minSegmentLength)
{
ptEndB = pt1;
}
else
{
ptEndB = Auxi_Geometry .PointToPoint (pt0,
Auxi_Geometry .Line_Angle (pt0, pt1), minSegmentLength);
}
PointF ptBase;
PointOfSegment typeOfNearest;
double fDist;
m_center = Auxi_Geometry .NearestPointOnSegment (pt, ptEndA, ptEndB,
out ptBase, out typeOfNearest, out fDist);
m_radius = r;
brush = brsh;
}
The usual thing for the technique of adhered cursor is that next to nothing is done inside the form itself where an object has to be
moved; the only needed thing there is to inform the caught object about the initial position of the mouse cursor at the moment of the catch. This allows
the caught object to remember the relative position of the cursor at the initial moment in order to keep it unchanged throughout the movement.
private void OnMouseDown (object sender, MouseEventArgs e)
{
if (mover .Catch (e .Location, e .Button))
{
GraphicalObject grobj = mover .CaughtSource;
if (grobj is SpotOnLineSegment)
{
(grobj as SpotOnLineSegment) .InitialMouseShift (e .Location);
}
else if (grobj is SpotOnArc)
{
(grobj as SpotOnArc) .InitialMouseShift (e .Location);
}
}
}
Whatever else is needed to keep the cursor at the same relative position is done inside the particular class of the spot. If you need
to restrict the movement of the spot along the horizontal or vertical segment, then you can use a standard clipping operation which imposes the restrictions
not on the moving of the object but on the moving of the mouse cursor. Because of this, the proposed example shows the new technique on the inclined lines with
which the standard clipping of the mouse cursor cannot be used.
Whatever is needed to keep the spot on the segment can be found in the SpotOnLineSegment.MoveNode() method.
public override bool MoveNode (int i, int dx, int dy, Point ptM,
MouseButtons catcher)
{
bool bRet = false;
if (catcher == MouseButtons .Left)
{
bRet = true;
PointF ptCenterNew = new PointF (ptM .X - dxMouseFromCenter,
ptM .Y - dyMouseFromCenter);
PointF ptBase, ptNearest;
PointOfSegment typeOfNearest;
double fDist = Auxi_Geometry .Distance_PointSegment (ptCenterNew, ptEndA,
ptEndB, out ptBase, out typeOfNearest, out ptNearest);
supervisor .MouseTraced = false;
Center = ptNearest;
Cursor .Position = form .PointToScreen (Point .Round (new PointF (
m_center .X + dxMouseFromCenter, m_center .Y + dyMouseFromCenter)));
supervisor .MouseTraced = true;
bRet = true;
}
return (bRet);
}
When the cursor tries to move the spot, the new proposed center of the spot is calculated according to the mouse position and the initial shifts of the cursor from the center of the spot.
PointF ptCenterNew = new PointF (ptM .X - dxMouseFromCenter,
ptM .Y - dyMouseFromCenter);
It may happen that this new point is just on the line, but the probability of such accurate moving of a spot is very low. More likely
that the cursor is moved somewhere along the segment so the position of the spot must be adjusted to the line. The exact new location of the spot on the
segment will be the nearest point of the segment from the proposed point ptCenterNew; the
Auxi_Geometry.Distance_PointSegment() method gives such point on the line (ptNearest).
double fDist = Auxi_Geometry .Distance_PointSegment (ptCenterNew, ptEndA,
ptEndB, out ptBase, out typeOfNearest, out ptNearest);
After the calculation of the new spot position on the
line, there is a standard (for this technique!) order of steps:
- The cursor is disconnected from the caught
object.
supervisor.MouseTraced = false;
- The spot is placed into calculated position on
the line.
Center = ptNearest;
- The cursor is placed at the known shift from the
new spot position.
Cursor .Position = form .PointToScreen (Point .Round (new PointF (
m_center .X + dxMouseFromCenter, m_center .Y + dyMouseFromCenter)));
- The cursor is linked again with the caught
object.
supervisor.MouseTraced = true;
Spot is moving on along the segment. The mentioned method Auxi_Geometry.Distance_PointSegment() calculates the nearest point not on the infinitive
line but on its segment between the known end points, so it will not allow to move the spot beyond those ends of the segment.
Now let us look at the case of the spot on the arc. The main idea is the same, but there are more calculations for this curved
trail and there is also one catch. Thanks to such traps, the programming is interesting and exciting.
Some fields in the class SpotOnArc are the same as in the previous
SpotOnLineSegment class; others are different because the trail has different shape.
public class SpotOnArc : GraphicalObject
{
Form form;
Mover supervisor;
PointF m_center;
int m_radius;
Color clr = Color .Red;
PointF ptCenter_Arc;
int radius_Arc;
RectangleF rcAroundCircle;
double minPositiveDegree_Arc, maxPositiveDegree_Arc;
There are all the needed methods in the MoveGraphLibrary.dll to calculate the point on the circle when the angle is
known or to calculate an angle for the known point; there are also methods to convert radians and degrees back and forth. To imagine and describe the
position of any point, I prefer to use degrees, while for calculations radians are used. The trail can be a full circle or only some part of it (an arc);
both cases are represented at figure 1. (In the initial version the big arc was really closed, but then I made a small gap in it to demonstrate
the trap that I am going to explain.) While initializing a SpotOnArc object, you declare the parameters of the spot and of its trail. Two angles are needed for
an arc: an angle from the center of a circle to one end point of the arc, and the sweep angle from this end to another one. Do not forget that the sign of
any angle is calculated in the normal way used in math – positive angles are going counterclockwise; I have already mentioned this in the chapter Rotation.
public SpotOnArc (Form frm, Mover mvr, PointF ptArcCenter, int nArcRadius,
double angleArcEnd_Degree, double angleArcSweep_Degree,
PointF pt, int r, Color clrSpot)
If the arc is shorter than the closed circle, then any movement of the spot must be checked for the possibility of going beyond the
end points. It was easier to do on the straight segment; on the arc we have to deal with the angles and the source of the small problem is the possibility of
jumping from the positive angles into negative or vice versa while moving along the arc. To organize the needed checking of angles, I use the
[minPositiveDegree_Arc,
maxPositiveDegree_Arc]
range; only the movement inside this range is allowed. In the most cases it would be enough but not in the case of nearly closed arc. The length of the gap depends on the
sweep degree of the arc and its radius. If you declare an arc with a very small gap angle (for nearly closed arc from
figure 1 the sweep angle is
354 degrees), then the gap is obvious. If you move the spot slowly, it will stop at the end point before the gap; if you try to move the spot faster,
chances are high that the spot will jump over the gap. With the really fast movement of the mouse the spot can jump over the gap of 15 degrees (maybe
more). This is not good at all; the trail is the trail; the spot is not supposed to move over the gaps; something must be done.
There can be different ways to prevent such jumping
over the ends of an arc; you can implement your own algorithm. My idea in
solving the problem of the gaps is based on setting the ranges of angles for
the first and the last quarters of the arc and not allowing to change the
position between these quarters. The additional checking of the jumps over the
gap is needed only for non-closed arcs; during the initialization of such arc
the special flag bCheckGap is set and two needed ranges are calculated.
public SpotOnArc (Form frm, Mover mvr, PointF ptArcCenter, int nArcRadius,
double angleArcEnd_Degree, double angleArcSweep_Degree,
PointF pt, int r, Color clrSpot)
{
… …
if (-360 < angleArcSweep_Degree && angleArcSweep_Degree < 360)
{
bCheckGap = true;
double quarter = (maxPositiveDegree_Arc - minPositiveDegree_Arc) / 4;
firstQuaterPositiveAngle = new double [] {
minPositiveDegree_Arc, minPositiveDegree_Arc + quarter };
lastQuaterPositiveAngle = new double [] {
maxPositiveDegree_Arc - quarter, maxPositiveDegree_Arc };
}
If the bCheckGap is set to true, then in the MoveNode() method an additional checking of the proposed movement
is organized.
public override bool MoveNode (int i, int dx, int dy, Point ptM, MouseButtons mb)
{
… …
if (bCheckGap)
{
… …
If it is found that currently the angle to the spot belongs to the first quarter of the arc and the proposed new spot position
belongs to the last quarter or vice versa, then such movement is not allowed, the spot is not moved anywhere, and the cursor is returned on its previous position inside the spot.
supervisor .MouseTraced = false;
Cursor .Position = form .PointToScreen (Point .Round (new PointF (
m_center .X + dxMouseFromCenter, m_center .Y + dyMouseFromCenter)));
supervisor .MouseTraced = true;
return (false);
At the beginning of this article I mentioned that everything is going to be movable. You can see yourself that in the Form_SpotsOnLinesAndArcs.cs
the colored spots are movable but their trails are not. It is done only to simplify the code and to focus the attention on the movement of the spots along
the trails. If you want to make everything movable, it is easy enough to do. For the movement of the straight segments and arcs you can look into the couple
of examples from the book. For example, the Form_SegmentOfLine.cs works with movable and changeable straight segments while for the arcs you can look
at the code of the Form_Arcs_FullyChangeable.cs. If you are going to change the current example to make everything movable then do not forget about two things.
- All the movable elements must be registered in the
mover’s queue. Because the spots must be moved along their trails then
these spots must be included into mover’s queue ahead of the trails.
- When the trail is moved, the position of its
associated colored spot must be adjusted. For a straight segment it can
be done with the
Auxi_Geometry.Distance_PointSegment() method while for arcs the
Auxi_Geometry.Ellipse_Point() method can be useful.
If I would have to make everything movable in this
example, I would organize two classes of complex objects trail + spot and
register such object with the mover by the IntoMover() method.
These things are well explained in the book.
This must be a short article, so I’ll skip a couple of
examples from the book and jump directly to the Form_SpotOnCommentedWay.cs.
- File: Form_SpotOnCommentedWay.cs
- Menu
position: Spots on lines – Spot on commented way
There are so many cases when you have to find your way
on a set of paths or roads. It can be a railroad system in Canadian Rockies,
or the floor plan of level 2 in the National Gallery, or some labyrinth which
you are going to explore, or simply a plan of your own house if you happen to
own something like Blenheim Palace. Anyway, you can think out a lot of
possibilities when something has to be moved by user(!) along the set of
trails on the screen. An object itself and the whole entourage can be very
picturesque but for the simplicity of the code let us deal in this example with
a set of pure lines and a small colored spot going along them. It is enough to
take into consideration only the straight segments and arcs as any complex
system of trails can be constructed of such elements.
In the name of the file with the new example you can
see the word Commented. When I tried to explain the right and wrong
movements of the small colored spot in the example Form_SpotOnConnectedSegments.cs (this is an example from the book) I had to add the
numbers of segments at the figure artificially because those numbers are not shown in the mentioned example. The new example – Form_SpotOnCommentedWay.cs
– uses much more complex set of trails and I change them from time to time, so it will be much easier for explanation and understanding to have all the
segments with some comments, for example, numbers.
To organize a way for the colored spot, three
different classes are used. One of them is an abstract class
Way_SegmentCommented which is used as
basic for two other classes.
public abstract class Way_SegmentCommented
{
protected WaySegmentType segment_type;
protected PointF ptStart, ptFinish;
protected CommentToCircle m_comment;
public abstract double Length { get; }
public abstract PointF Center { get; }
public abstract void Draw (Graphics grfx, Pen pen, bool bMarkEnds,
Color clrEnds);
public abstract double DistanceToSegment (PointF pt, out PointF ptNearest);
public abstract CommentToCircle Comment { get; }
While drawing new segments, their end points can be
marked with different color; this makes easier the understanding of the whole
set of segments.
New segments have a Center property.
For the arc segment it is the center around which the arc is constructed; for
the straight segment it is the middle point between its ends.
Straight segments belong to the
Way_LineSegmentCommented class.
public class Way_LineSegmentCommented : Way_SegmentCommented
{
double m_angle;
static double minLength = 10;
public Way_LineSegmentCommented (Form form, PointF pt0, PointF pt1,
double angleToC_Degree, double coefToCenter,
string txt_Cmnt, Font fnt_Cmnt, double angleDegree_Cmnt, Color clr_Cmnt)
{
segment_type = WaySegmentType .Line;
ptStart = pt0;
m_angle = Auxi_Geometry .Line_Angle (pt0, pt1);
if (Auxi_Geometry .Distance (pt0, pt1) >= minLength)
{
ptFinish = pt1;
}
else
{
ptFinish = Auxi_Geometry .PointToPoint (ptStart, m_angle, minLength);
}
PointF center = Auxi_Geometry .Middle (ptStart, ptFinish);
m_comment = new CommentToCircle (form, Point .Round (center),
Convert .ToInt32 (Length / 2), angleToC_Degree,
coefToCenter, txt_Cmnt, fnt_Cmnt, angleDegree_Cmnt, clr_Cmnt);
}
Curved parts of the way are represented by the objects of the Way_ArcSegmentCommented class.
public class Way_ArcSegmentCommented : Way_SegmentCommented
{
PointF m_center;
float m_radius;
double angleStart, angleSweep;
RectangleF rcAroundCircle;
double angleStart_Deg, angleSweep_Deg;
static double minLength = 15;
static float minArcRadius = 20;
Any segment of the way might have a comment of the CommentToCircle class. This class is derived from the TextMR class and is included into the
MoveGraphLibrary.dll but it is used not too often so I think I need to mention the rules for positioning CommentToCircle objects.
It is obvious from the name that such comments are used with the circles. The position of comment (its central point) is described by an angle from the
center of the “parent” circle and additional coefficient. When the coefficient is inside the [0, 1] range, then the comment is inside the circle: 0 means the
center of the circle, while coefficient 1 puts the comment on the border. When the coefficient is greater than 1, then the comment is placed outside the
circle and the coefficient means the distance in pixels from the border of the circle to the comment.
When the comment of the CommentToCircle class is used with the arc, there are no problems in understanding all the parameters because there is a circle along the border of
which this arc is painted. When you have a straight segment, then you need to imagine the circle with the center in the middle of segment and the radius
equal to half of the length of this segment. Thus, both end points of straight segment are on the border of this imaginable circle and you position the
comment in relation to this imaginable circle.

The Form_SpotOnCommentedWay.cs allows to work with different ways by changing the number of segments; there is a combo box to do it. This example starts with
four segments connected one after another (figure 2).

If you increase gradually the number of segments then somewhere throughout this process you have a system of 11 segments (figure 3).
Figure 4 shows the maximum system of 18 segments.

When you develop an application in which a colored spot has to be moved along some system of trails then the whole task
can be divided into two big parts. The first one is the design of the trails; the second one is the movement of an object along those trails. The second
task is nearly the same as was discussed in the previous example Form_SpotOnLinesAndArcs.cs. The details of such movement are mostly explained with the previous example and
the only addition to be thought out is the movement from one segment to
another. Think about this task as the movement of a train along the rails. If
the train (the colored spot) is somewhere on segment seven then it can go
either to segment eight or four but it cannot go directly to segment one though
the lines of segments one and seven cross on the screen. If you think about
the whole thing as the railroads then a normal train going over the bridge
(segment 7) does not jump to another trail (segment one) going underneath.
The trail system in the Form_SpotOnCommentedWay.cs can be changed at any moment, so the position of the spot must be adjusted to
it. Certainly it is done in this example but the main thing is such design that for any position of the colored spot it is easy to find to which segments
it can move further on. Three lists of segments are used in the program:
List<Way_SegmentCommented> maximumWay = new List<Way_SegmentCommented> ();
List<Way_SegmentCommented> segmentsAll = new List<Way_SegmentCommented> ();
List<Way_SegmentCommented> segmentsAvailable = new List<Way_SegmentCommented> ();
maximumWay contains the full list of segments. This list is
populated only once by the SetMaximumWay() method
and is used as a source of segments throughout the whole work of the Form_SpotOnCommentedWay.cs example. You can see from the code of the
SetMaximumWay() method that each segment has a comment that shows the
number of the segment; these comments are seen at figures 2, 3, and 4.
private void SetMaximumWay ()
{
maximumWay .Add (new Way_LineSegmentCommented (this, new PointF (100, 200),
new PointF (250, 200), 90, 0.2, "0", fntCmnts, clrCmnts));
maximumWay .Add (new Way_LineSegmentCommented (this,
maximumWay [0] .PointFinish, -20, 220, 130, 0.3, "1",
fntCmnts, clrCmnts));
PointF ptEnd = maximumWay [1] .PointFinish;
double angle = (maximumWay [1] as Way_LineSegmentCommented) .Angle;
double angleToCenter = angle - Math .PI / 2;
double radius = 180;
PointF ptCenter = Auxi_Geometry .PointToPoint (ptEnd, angleToCenter, radius);
maximumWay .Add (new Way_ArcSegmentCommented (this, ptEnd, ptCenter, -100,
50, 0.9, "2", fntCmnts, clrCmnts));
… …
maximumWay .Add (new Way_ArcSegmentCommented (this, ptA, center,
Auxi_Convert .RadianToDegree (angle) - 90,
110, 0.85, "17", fntCmnts, clrCmnts));
}
segmentsAll contains all the segments shown at each particular
moment. The number of available segments can be changed (there is a control to
do it) and the list is populated by the SetTrails() method.
private void SetTrails (int nTrails)
{
segmentsAll .Clear ();
for (int i = 0; i < nTrails; i++)
{
segmentsAll .Add (maximumWay [i]);
}
}
segmentsAvailable contains at each moment only few segments. Depending
on the current configuration of the shown segments (segmentsAll) and the position of the spot, this list contains
between two and four elements (for the current system of segments), but the
population of this list is an interesting process. At any moment this list
contains only the segment currently used by the spot and the connected segments
to which the spot can move directly from this one.
Let us check how it works when the Form_SpotOnCommentedWay.cs is started.
public Form_SpotOnCommentedWay ()
{
InitializeComponent ();
mover = new Mover (this);
fntCmnts = new Font ("Times New Roman", 12, FontStyle .Bold);
clrCmnts = Color .Blue;
ccNumber = new CommentedControl (this, numericUD_Trails, Side .E, "Trails");
SetMaximumWay ();
SetTrails (4);
spot = new SpotOnCommentedWay (this, mover, segmentsAll,
new PointF (400, 100), 7, Color .Magenta);
int iUsedSeg = spot .CurrentlyUsedSegment;
PrepareAvailableWay (iUsedSeg);
spot .SetWay (segmentsAvailable);
iCurrentlyUsedFromAvailable = spot .CurrentlyUsedSegment;
RenewMover ();
}
maximumWay is populated by the SetMaximumWay() method
and the number of segments is limited to four by the SetTrails() method. Then the spot is initialized.
spot = new SpotOnCommentedWay(this, mover, segmentsAll,
new PointF (400, 100), 7, Color .Magenta);
Among other parameters, the spot gets the currently used system of segments –
segmentsAll. Though another parameter declares the point where
the spot must appear, this point is used only as the first approximation. The spot is positioned there but after it the nearest point on the available
segments is found and the spot is moved to this point. Thus, the spot cannot be placed anywhere except the available segments.
After the spot is placed on some segment, it can
return the number of this segment.
int iUsedSeg = spot .CurrentlyUsedSegment;
With this known number and currently used system of segments, the short list
of really available segments at this moment – segmentsAvailable –
can be populated by the PrepareAvailable() method. This short list
always includes the segment where the spot is positioned now and the segments to
which the spot can move directly from this segment. Those available segments
depend on the current configuration.
private void PrepareAvailableWay (int iCurrentlyUsedSegment)
{
segmentsAvailable .Clear ();
numbersAvailable .Clear ();
int nTrails = Convert .ToInt32 (numericUD_Trails .Value);
MakeSegmentAvailable (iCurrentlyUsedSegment);
switch (iCurrentlyUsedSegment)
{
case 0:
if (nTrails >= 2) MakeSegmentAvailable (1);
if (nTrails >= 6) MakeSegmentAvailable (5);
break;
case 1:
MakeSegmentAvailable (0);
if (nTrails >= 3) MakeSegmentAvailable (2);
break;
… …
This short list - segmentsAvailable - contains all the available, at the moment, segments for the spot.
All other segments are not available so they do not exist for the spot. Then
this short list is sent to the spot as the full system of segments and the spot
returns the number of the occupied segment from this short list.
spot .SetWay(segmentsAvailable);
iCurrentlyUsedFromAvailable = spot.CurrentlyUsedSegment;
Similar exchange of information between the spot and the form happens when the spot is moved.
private void OnMouseMove (object sender, MouseEventArgs e)
{
if (mover .Move (e .Location))
{
GraphicalObject grobj = mover .CaughtSource;
if (grobj is SpotOnCommentedWay)
{
int iNewSegment = spot .CurrentlyUsedSegment;
if (iNewSegment != iCurrentlyUsedFromAvailable)
{
PrepareAvailableWay (numbersAvailable [iNewSegment]);
spot .SetWay (segmentsAvailable);
iCurrentlyUsedFromAvailable = spot .CurrentlyUsedSegment;
}
}
Invalidate ();
}
}
When the spot is moved, its MoveNode() method is used. The nearest point on the available segments is found; the spot is moved into this point, and the number of this
segment is returned into the OnMouseMove() method.
int iNewSegment = spot .CurrentlyUsedSegment;
If this number differs from the previously occupied segment, then it means that the spot has moved from one segment to another, the
new available system of segments must be prepared; this new system of available segments is sent to the spot, and the spot returns the number of the newly
occupied segment among the new set of available segments.
if (iNewSegment != iCurrentlyUsedFromAvailable)
{
PrepareAvailableWay (numbersAvailable [iNewSegment]);
spot .SetWay (segmentsAvailable);
iCurrentlyUsedFromAvailable = spot .CurrentlyUsedSegment;
}
There are two reasons that there is no code to prevent
the jumps over the end points of arcs in the Form_SpotOnCommentedWay.cs. The
described algorithm allows to move only to the available segments, while the
problem of jumping over the gaps in the arcs is solved by not using the arcs
with the big sweep angles. If you need to use a long arc close to a full
circle, divide such arc into three or four. You can see such solution in the Form_SpotOnCommentedWay.cs with segments 2, 3, and 4 (figure 4). These
three arcs belong to the same circle so I could easily unite them into one arc,
for example, with number 2. But then some people will try to move the colored
spot really quickly right and down from the shown position and instead of going
farther on along the segment 7 (in current version) it can jump to another end
of the same segment 2.
To solve this problem, it would be enough to divide
big arc inito two, for example, by uniting segments 2 and 3. Because I needed
a point of connection for segment 17, I decided to divide my nearly full circle
into three parts.
In both of the previous examples a colored spot moves
along the well visible trail, but this is not a mandatory thing. Nowhere in
the code of those examples you can find a requirement that the segments of the
way must be painted. They are painted, but you can easily comment some lines
in the
OnPaint() method and nothing will change
at all; the spot will continue to move along the invisible trails and this will
be a strange thing. Well, it is a strange thing for this Form_SpotOnCommentedWay.cs example but it is an ordinary and expected thing if
you deal with movement in some labyrinth. To demonstrate such a thing there is
the next example Form_LabyringthForDachshund.cs.
- File: Form_LabyrinthForDachshund.cs
- Menu position: Spots on lines – Labyrinth for a
dachshund
I am familiar with one nice dachshund who likes to
investigate all dark holes and enigmatic passes, so I decided to unite the idea
of labyrinth from the Form_BallInLabyrinth.cs example (from the book!)
with some code from the previous Form_SpotOnCommentedWay.cs example and to construct an interesting labyrinth for
this clever dog. If you ever saw a single dachshund
you understand that in the narrow curved tunnels the tail of this dog is
usually two turns back from its nose, so, while going through the labyrinth,
this dog is represented by a colored spot, while the moment she steps out she
immediately turns into a nice dog (figure 5).

The movement of the colored spot inside the labyrinth is organized in the same way as in the previous example Form_SpotOnCommentedWay.cs only in this new example it is a bit simpler.
Labyrinth is the same all the time, so it is enough to have two lists of segments: one includes all the segments of the labyrinth
and another only the segments available at each particular moment.
List<Way_SegmentCommented> way;
List<Way_SegmentCommented> segmentsAvailable;
The segments inside the labyrinth are not shown, but
there are commented lines in the OnPaint() method.
Turn these lines into the working code and the segments will be painted. It
does not matter whether the segments are painted or not; the colored spot can
go only along them. In this example I use only straight segments of the Way_LineSegmentCommented class. If you
want, you can insert the Way_ArcSegmentCommented segments
on the curves; especially on those where there are no variants and the 90
degree turn is the only way to go on.
The Form_LabyrinthForDachshund.cs is not the only example with labyrinths in the book World of Movable Objects. There
are several more examples and for each of them the design of labyrinth is not the main thing but needs the programming efforts. Also each of those examples
work with one particular labyrinth that is already coded and thus fixed. Each
of the examples is included into the book to demonstrate some features of the
moving process, but each of those examples has such a limitation.
When there is an easy to understand and implement
technique of moving an object inside a labyrinth, then it would be nice to have
an easy to use technique with which any user can design any labyrinth just in
seconds or minutes. I don’t think that small kids have to spend the time in
front of the computer screen, but they have a habit to come and do the same
things as grown ups are doing. Imagine that you can design a new labyrinth on
the screen just in seconds and then a small person can try to move the spot
through this just constructed labyrinth. This would be not the worst way of
using a computer and this is what you can find in the next example.
There is one major difference between the previous
examples and the next one. Regardless of whether the way was visible or not in
the previous examples, it was always predetermined. The system of trails could
be a complex one, but the colored spot could not go anywhere outside those
predetermined lines. The walls in the Form_LabyrinthForDachshund.cs are
used as an entourage and nothing else. In the next example there is no
predetermined set of trails and the walls restrict the movements of the colored
spot.
- File: Form_SpotInManualLabyrinth.cs
- Menu position: Between walls – Spot in manual
labyrinth
First, let us formulate the requirements for the
labyrinth design.
- A labyrinth is designed of an arbitrary set of
straight walls.
- Any wall can be modified, duplicated, or deleted.
- A set of walls can be united into a group and the
same commands (modify, duplicate, or delete) can be applied to all the
walls of such group.
- The constructed labyrinths can be saved as binary
files and restored at any moment for later use.
It is not a surprising thing that even very
interesting examples can be based on relatively simple elements. Each wall in
our new labyrinths is going to be an object of the LineSegment class – a segment of a straight line with the
possibility of the length change. Any wall can be also rotated; the rotation
of a segment goes around its middle point. A straight line is really a simple
element: only two end points are needed and a pen to draw the line between
these points. To avoid the accidental disappearance of an element, there is a
limit on minimal length of a wall.
public class LineSegment : GraphicalObject
{
PointF ptA, ptB;
Pen m_pen;
static int minLen = 10;
The cover of such object consists of three nodes: two
circular nodes at the end points are used to change the length while the strip
node along the whole length of an element allows to move it forward and rotate.
public override void DefineCover ()
{
float radius = Math .Max (3, m_pen .Width / 2);
cover = new Cover (new CoverNode [] {new CoverNode (0, ptA, radius),
new CoverNode (1, ptB, radius),
new CoverNode (2, ptA, ptB, radius)});
}
The colored spot to be moved inside a labyrinth is
also simple. An object of the Spot_Restricted class is a
small circle with a radius that can be changed inside the [3, 12] range.
public class Spot_Restricted : GraphicalObject
{
Form form;
Mover supervisor;
PointF m_center;
int m_radius = 5;
Color m_color = Color .Red;
List<LineSegment> walls = new List<LineSegment> ();
static int radMin = 3;
static int radMax = 12;
The cover of such spot consists of a single circular
node covering the whole element.
public override void DefineCover ()
{
cover = new Cover (new CoverNode (0, m_center, Math .Max (m_radius, 5)));
}
To make the catching of such spot easier, the radius
of the node is never less than five pixels. Thus, for the smallest spot the
node is bigger than the spot itself and such spot can be grabbed not only by
any point inside its border but also at the points which are outside the spot
but close to its border. The spot can be grabbed at different points but at
the moment of catching the cursor is moved to the center of the spot and is
adhered to this central point throughout the whole process of movement.
public void StartMoving ()
{
supervisor .MouseTraced = false;
Cursor .Position = form .PointToScreen (Point .Round (m_center));
supervisor .MouseTraced = true;
}
Now let us see how all the things work inside the Form_SpotInManualLabyrinth.cs.
When you open this form for the first time, it is nearly empty: there is a
lonely colored spot in view and nothing else. The only way to start building a
labyrinth is to call the menu at any empty place (figure 6).

Well, to be correct, this is the view of the menuOnEmpty when there is at least one wall inside the form.
Without any walls in view, only the first command of this menu is enabled; this
command is always enabled and just now we are interested in this command. By
clicking the first command of this menu you add the new wall. At the beginning
there are no other walls, so the new one will be the only one in view.
private void Click_miAddNewWall (object sender, EventArgs e)
{
LineSegment segment = new LineSegment (ptMouse_Up,
new PointF (ptMouse_Up .X + 50, ptMouse_Up .Y + 70), penWalls);
AvoidSpotSegmentOverlap (segment);
segments .Add (segment);
RenewMover ();
Invalidate ();
}
Because the length, position, and angle of any wall
can be easily changed, this new wall can be transformed to whatever you need.
Any wall can be modified and positioned independently of all others; in such
way any labyrinth can be constructed; figure 7 shows one of the
infinitive variants

The second way to add new wall is to call the context menu on any existing wall (figure 8) and to use its command Duplicate.

The inclination of any line (wall) can be easily changed by simple rotation but the same menu contains a pair of commands to
make the touched wall strictly horizontal or vertical. Another menu command allows to call a small tuning form and to change with its help the view of any
line (color, width, and style) so not all the walls must look in the same way. But if you like the new view of some wall and would like to make all others
similar, call this menu on the wall with the preferable view and select its Use as sample command.
Another way to change the design, and this way is even more powerful, is to use the group. Such group – of the
GroupOfSegments class – can contain an arbitrary number of segments
(at least one) and looks like a slightly rounded frame around all its inner elements.
public class GroupOfSegments : GraphicalObject
{
List<LineSegment> lines = new List<LineSegment> ();
int spaceToFrame = 10;
Pen penFrame;
If you need to organize some segments into a group, you have to press the left button at an empty place:
private void OnMouseDown (object sender, MouseEventArgs e)
{
ptMouse_Down = e .Location;
if (mover .Catch (e .Location, e .Button))
{
… …
}
else
{
if (e .Button == MouseButtons .Left)
{
if (group != null)
{
FreeWalls ();
}
bTemporaryFrame = true;
}
}
ContextMenuStrip = null;
}
and move the mouse without releasing the pressed button.
private void OnMouseMove (object sender, MouseEventArgs e)
{
ptMouse_Move = e .Location;
if (mover .Move (e .Location))
{
… …
}
else
{
if (bTemporaryFrame)
{
Invalidate ();
}
}
}
At any moment the rectangular frame is shown; the
point of initial press and the current mouse point are used as the opposite
corners of this rectangle.
private void OnPaint (object sender, PaintEventArgs e)
{
Graphics grfx = e .Graphics;
… …
if (bTemporaryFrame)
{
grfx .DrawRectangle (penFrame,
Auxi_Geometry .RectangleAroundPoints (ptMouse_Down, ptMouse_Move));
}
}
When at last the button is released, then the
temporary frame is gone, but if at this moment there are some segments (at
least one) inside the temporary frame, then the group is organized and it
contains all those segments that were rounded.
private void OnMouseUp (object sender, MouseEventArgs e)
{
ptMouse_Up = e .Location;
double dist = Auxi_Geometry .Distance (ptMouse_Down, ptMouse_Up);
if (mover .Release ())
{
… …
}
else
{
if (e .Button == MouseButtons .Left)
{
if (bTemporaryFrame)
{
Rectangle rc = Auxi_Geometry .RectangleAroundPoints
(ptMouse_Down, e .Location);
List<LineSegment> segmentsInFrame = new List<LineSegment> ();
for (int i = segments .Count - 1; i >= 0; i--)
{
if (rc .Contains (Rectangle .Round
(segments [i] .RectAround)))
{
segmentsInFrame .Insert (0, segments [i]);
segments .RemoveAt (i);
}
}
if (segmentsInFrame .Count > 0)
{
group = new GroupOfSegments (segmentsInFrame, penFrame);
RenewMover ();
}
bTemporaryFrame = false;
Invalidate ();
}
… …
With this group a lot of things can be done. Forward
movement and rotation of the group with all its elements can be started by an
ordinary mouse press inside the group (left button press starts forward
movement, right button press starts rotation) while other things are done via
the commands of the context menu that can be called inside the group.
A GroupOfSegments object
is simple and its cover is very simple and consists of a single rectangular
node slightly bigger than the frame. This means that the group can be grabbed
for moving by any inner point or any point in the vicinity of the frame.
public override void DefineCover ()
{
Rectangle rc = rcFrame;
rc .Inflate (3, 3);
cover = new Cover (rc, Resizing .None);
}
The group is not a resizable object by itself, so it is impossible to change its sizes by moving its borders, but the sizes of the
group depend on the positions of all the inner elements. This means that any move of any segment belonging to the group calls the update of the group.
private void OnMouseMove (object sender, MouseEventArgs e)
{
ptMouse_Move = e .Location;
if (mover .Move (e .Location))
{
GraphicalObject grobj = mover.CaughtSource;
if (grobj is LineSegment)
{
if (group != null && grobj .ParentID == group .ID)
{
group .Update ();
}
}
… …
The update of the group consists of recalculating of its frame and cover.
public void Update ()
{
CalcFrame ();
DefineCover ();
}
When you duplicate any segment belonging to the group,
the new segment is also included into the group. As the duplicate of any wall
is placed slightly aside from the original, then such action often increases
the size of the group.
private void Click_miDuplicate (object sender, EventArgs e)
{
LineSegment segment = segmentPressed .Copy;
segment .Move (30, 30);
AvoidSpotSegmentOverlap (segment);
if (group != null && segmentPressed .ParentID == group .ID)
{
group .AddSegment (segment);
}
else
{
segments .Add (segment);
}
RenewMover ();
Invalidate ();
}
The forward movement of the group orders the synchronous movement of the inner elements so their relative positions do not change.
public override void Move (int dx, int dy)
{
rcFrame .X += dx;
rcFrame .Y += dy;
foreach (LineSegment elem in lines)
{
elem .Move (dx, dy);
}
}
The group can be also rotated, but here the situation
is a bit more complex than in the case of a single wall rotation. Any segment
inside the group can be rotated individually; such rotation goes around the
middle point of the caught segment and calls the update of the group. The
rotation of the group as a whole goes around its central point and it differs
from the synchronous rotation of all elements around their central points (it
is not a ballet or the type of synchronous rotation demonstrated in the Form_SpottedTexts.cs
in the chapter Texts of the book). When the group is pressed for
rotation (right mouse press), its GroupOfSegments.StartRotation()
method is called.
private void OnMouseDown (object sender, MouseEventArgs e)
{
ptMouse_Down = e .Location;
if (mover .Catch (e .Location, e .Button))
{
GraphicalObject grobj = mover .CaughtSource;
if (e .Button == MouseButtons .Left)
{
… …
}
else if (e .Button == MouseButtons .Right)
{
if (grobj is LineSegment)
{
(grobj as LineSegment) .StartRotation (e .Location);
}
else if (grobj is GroupOfSegments)
{
(grobj as GroupOfSegments) .StartRotation (e .Location);
}
}
… …
Each segment of the group is based on two end points. All the segments are going to rotate around the same point – the central point
of the group, so for each end point of each segment its own radius and compensation angle must be calculated at the starting moment of the group’s
rotation. These calculations are done in the GroupOfSegments.StartRotation() method.
public void StartRotation (Point ptMouse)
{
compensation = new double [2 * lines .Count];
radius = new double [2 * lines .Count];
ptMiddle = Auxi_Geometry .Middle (rcFrame);
double angleMouse = Auxi_Geometry .Line_Angle (ptMiddle, ptMouse);
for (int i = 0; i < lines .Count; i++)
{
compensation [i * 2] = Auxi_Common .LimitedRadian (angleMouse –
Auxi_Geometry .Line_Angle (ptMiddle, lines [i] .Point_A));
compensation [i * 2 + 1] = Auxi_Common .LimitedRadian (angleMouse –
Auxi_Geometry .Line_Angle (ptMiddle, lines [i] .Point_B));
radius [i*2] = Auxi_Geometry .Distance (ptMiddle, lines [i] .Point_A);
radius [i*2+1] = Auxi_Geometry.Distance (ptMiddle, lines [i] .Point_B);
}
}
In this way the group can be moved forward and rotated; other possibilities are available
via the commands of its context menu (figure 9). Among others, there are two commands that allow to construct labyrinths much faster; these are the
commands to duplicate all the walls of the group. Depending on the used command, the duplicates are placed either to the:

right of the existing set of segments or below so in both cases none of the new segments overlap with any of the existing segments of the group.
There is one thing that must be not forgotten when you add new segments, move and release them, or duplicate: a segment can appear at
the place of the colored spot and something must be done in such situation. From my point of view the solution is obvious: if it happens, such segment must
be moved aside. This is done in the AvoidSpotSegmentOverlap() method.
private bool AvoidSpotSegmentOverlap (LineSegment segment)
{
bool bMove = false;
if (Auxi_Geometry .Distance_PointSegment (spot .Center, segment .Point_A,
segment .Point_B) <= spot .Radius + segment .Pen .Width / 2)
{
segment .Move (0, 30);
bMove = true;
if (Auxi_Geometry .Distance_PointSegment (spot .Center,
segment .Point_A, segment .Point_B) <= spot .Radius)
{
segment .Move (30, 0);
}
if (group != null && segment .ParentID == group .ID)
{
group .Update ();
}
}
return (bMove);
}
An additional remark about one command from the menu on the walls (figure 8). I already mentioned that the view of the
pressed wall can be spread on other walls by using the command Use as sample. The result of this command slightly depends on whether the pressed wall is inside the group or not.
- If it is inside the group, then only the walls inside
the group are changed.
- If it is not in the group, then only the walls
that are not included into the group are changed.
Looks like I have explained everything about the
design and change of an arbitrary labyrinth but forgot to write about the
movement of colored spot in the labyrinth which is the main thing in this
example. As usual, we have to look at the code of three mouse events in the Form_SpotInManualLabyrinth.cs
– the OnMouseDown(), OnMouseMove(), and OnMouseUp() methods – and on the
MoveNode()
method of the involved class – the Spot_Restricted.MoveNode()
method.
The movement of the spot starts when this spot is
pressed by the left button.
private void OnMouseDown (object sender, MouseEventArgs e)
{
ptMouse_Down = e .Location;
if (mover .Catch (e .Location, e .Button))
{
GraphicalObject grobj = mover .CaughtSource;
if (e .Button == MouseButtons .Left)
{
if (grobj is Spot_Restricted)
{
segmentsAll .Clear ();
if (group != null)
{
segmentsAll .AddRange (group .Elements);
}
segmentsAll .AddRange (segments);
spot .Walls = segmentsAll;
spot .StartMoving ();
}
}
… …
At this moment a group around some walls may or may not exist, but this fact has nothing to do with the restrictions on the spot
movement. If there is a group then the visible border of this group is only a reminder for the user about the group of walls that can be moved and changed
simultaneously or duplicated by a single command. For the colored spot the border of the group does not mean anything and the walls inside or outside
the group work as a restriction for movement in the same way. Thus, a united List of all the walls – segmentsAll – is organized to be used
as barriers for further movements. This united List includes walls from inside (group.Elements) and outside (segments) the
group. The spot gets this List via the Spot_Restricted.Walls property.
segmentsAll .Clear ();
if (group != null)
{
segmentsAll .AddRange (group .Elements);
}
segmentsAll .AddRange (segments);
spot .Walls = segmentsAll;
At the same moment the mouse cursor is moved to the central point of the colored spot in order to avoid dealing with the initial
mouse shifts throughout the whole process of movement. This is done by the Spot_Restricted.StartMoving() method.
spot.StartMoving ();
In the OnMouseMove() method of the form the Spot_Restricted object is
not mentioned so we have to look into the Spot_Restricted.MoveNode() method to find out what happens with the colored spot throughout the movement.
public override bool MoveNode (int i, int dx, int dy, Point ptM,
MouseButtons catcher)
{
bool bRet = false;
if (catcher == MouseButtons .Left)
{
LineSegment wall;
for (int j = 0; j < walls .Count; j++)
{
wall = walls [j];
if (Auxi_Geometry .Distance_Segments (m_center, ptM, wall .Point_A,
wall .Point_B) <= m_radius + wall .Pen .Width / 2)
{
supervisor .MouseTraced = false;
Cursor .Position = form .PointToScreen (Point .Round (m_center));
supervisor .MouseTraced = true;
return (false);
}
}
Center = ptM;
bRet = true;
}
return (bRet);
}
The checking of the possibility of proposed movement is really easy. The mouse is moved somewhere by the user and this new mouse
position must become the new central point of the spot. The minimal allowed distance between the central point of the spot and the central line of the wall is the
sum of the radius and half the width of this wall. This checking must be done for each wall of the labyrinth. Walls are not moved throughout the movement of
the spot and the current List of walls was just sent to the spot at the initial moment of its movement. If any wall prevents the proposed
movement of the spot then the mouse cursor is returned to the previous position. As usual, this is done with the temporary disconnection of the link
between the mover and the object under move.
In one of the examples in the book I have demonstrated
that one more checking is needed: if you try to move the colored spot really
quickly, it can go through the wall. Because of that possibility, there is an
additional checking in the BallSV class
(look for it in the Form_BallInLabyrinth.cs example of the book). Maybe
I am not so fast now, but I can’t reproduce the movement of the colored spot
through any wall in the Form_SpotInManualLabyrinth.cs and excluded an
additional checking from the code. If you are more successful with reproducing
this situation in the current example you now know where to look for the
additional checking to improve the code.
When the spot is released it can be released only on
an empty place but with the release of a wall the situation is different. A
wall can be moved anywhere and it can be released while overlapping the colored
spot. In this case the wall is moved slightly aside in order to avoid such
overlapping. The same overlapping of some wall and the colored spot can occur
when not a single wall but a group is moved and released; in both cases the
AvoidSpotSegmentOvelap() method must be used.
private void OnMouseUp (object sender, MouseEventArgs e)
{
ptMouse_Up = e .Location;
double dist = Auxi_Geometry .Distance (ptMouse_Down, ptMouse_Up);
if (mover .Release ())
{
GraphicalObject grobj = mover .WasCaughtSource;
if (grobj is LineSegment)
{
LineSegment segment = grobj as LineSegment;
if (AvoidSpotSegmentOverlap (segment))
{
Invalidate ();
}
}
else if (grobj is GroupOfSegments)
{
foreach (LineSegment segment in group .Elements)
{
if (AvoidSpotSegmentOverlap (segment))
{
Invalidate ();
}
}
}
… …
Though the examples of this article use similar
technique of adhered mouse cursor during the movements of some objects they use
this technique in slightly different ways.
One is the situation with the predetermined set of
trails and an object that can be moved only along those trails. For each
movement of the mouse cursor, the nearest allowed position on the trails is
calculated, an object is moved into this position, and throughout the position
adjustment the link between the mover and the object under move must be
temporary disconnected. The objects around the trails have nothing to do with
the movement and are used only as an entourage.
Another is the case without predetermined trails and
in this case the objects around are used to restrict the movements. If any of
those objects does not allow the movement proposed by the move of the mouse
cursor, then an object is not moved, the cursor must be returned to the
previous position, and for this back movement of the cursor the same temporary
disconnection between the mover and the object is organized.
