BrainFix, the language that translates to fluent Brainfuck

 

• Download source code from the project-pages.

2022 UPDATE

ATTENTION: this project has been given new life. Though a lot of the contents of this article are still relevant and true (even though not all the formatting has survived through the past 10 years), a more up-to-date, better, improved, newer, awesomer version of the software is available on my Github page. The readme contains a description of the language (many breaking syntax changes). The article below can be referred to for the BF-algorithms that have been implemented. 

Back to 2013....

Introduction to BrainFuck

BrainFuck is an esoteric programming language devised by Urban Müller in 1993. It is a Turing Complete language, because it provides sufficient tools to solve any computational task. However, it can also be called a true Turing tar-pit, in that it is of no actual practical use despite the fact that it is so easy to learn. The reason it is so easy to learn is mainly due to its simplicity: only 8 operations are defined by the language, resembling the workings of a Turing Machine. An (infinite) array is assumed, together with a pointer to some element of the array. The operations that can now be performed are the following (the equivalent C-code displayed between parentheses):

• > Move the pointer one position to the right. (++ptr;)
• < Move the pointer one position to the left. (--ptr;)
• + Increment the value pointed to by 1. (++*ptr;)
• - Decrement the value pointed to by 1. (--*ptr;)
• . Print the value in the current cell to the output. (putchar(*ptr);)
• , Read a value from the input and store it in the current cell. (*ptr = getchar();)
• [ If the current value is zero, the program skip the code between [ and ]. (while (*ptr) {)
• ] Program flow will move back to the corresponding ] (}).

Background

The language described below was defined using Bisonc++ and Flexc++ by Frank B. Brokken.

Introduction to BrainFix

It is a difficult task to write complex algorithms using the limited toolset offered by BrainFuck, so and intermediate language was designed to be able to translate readable source-code to (almost) unreadable BrainFuck code. I have called this language BrainFix, as it fixes the impracticalities of the BrainFuck but still produces valid code. The language inherits its syntax from Matlab, C, and Python. A complete program must at least have a main() function defined in one of its source-files. The smallest possible BrainFix program, that does nothing at all, is the following:

function main() {}

The function body may contain expressions that are built from variables, keywords, constants, operators and function-calls and are terminated by a semicolon (;). Each of these features is discussed in the coming sections. If this manual came with a package distributed by myself, the examples are included as .bfx files. If not, you can easily copy and paste the code yourself!

Hello World

Let us start with the classical “Hello World!” example. BrainFix supports string literals. This allows us to print strings to the standard output using the prints keyword, as illustrated below. In order to print a newline, the escape sequence \n can be embedded in the string (as of version 0.41).

/* hello.bfx */  
 
function main()  
{  
    prints "Hello World!\n";  
}

Printing

There are four different print keywords in BrainFix: print, printc, printd, prints. In the previous section, we have already seen how to print strings using the prints keyword, and how to print a newline using an escape character. The print and printc commands print the character representation (according to your system’s locale) of the expression it is being passed. Therefore one could also use printc 10; to print a newline. The printd command will print the decimal value of the expression, but it only supports 3 digits. The BrainFuck language assumes an array of single bytes, therefore 3 digits should be enough to print all output.

Scanning

Using the scan keyword, a value is read from standard input, and stored in the variable passed to the scan command (e.g. scan x;). It is currently only possible to scan decimal values.

Variables and Keywords

The variables in BrainFix start with a letter (lower- or uppercase), followed by any number of alphanumerics (no underscores). They need not be declared or allocated and their type is deduced by the compiler. BrainFix can handle three types of variables: integers/characters, string-literals and arrays. Integers and characters (between single quotes, e.g., 'a') are treated exactly the same, and string-literals are just a special case of array: an array of characters with a terminating 0-character. Only positive integer values are supported. Negative values will not be recognized by the parser and subtractions that would otherwise result in negative values will now result in 0. A value is parsed as a string when it appears within double quotes (as illustrated in the “Hello World!” example). Of course, the BrainFix keywords listed below may not be used as variables.

Escape sequences can be used to print characters that have a special meaning in the BrainFix language. For example, in order to print double quotation-marks within a string, one can do the following:

prints "Hello \"World\"!\n";

When the escaped character has no special meaning, its regular representation is used (e.g. \j is parsed as j).

Keywords:

print   printc  printd
prints  scan    if
else    for     array

Functions

A BrainFix program consists of functions, one of which must be named main. This is the function that is executed when the program is started. From main(), other functions can be called that are defined in either the same sourcefile or another. When the other function is defined in a different sourcefile than main(), be sure to pass this file to the BrainFix compiler (bfx). Functions may receive arguments (by value) and are able to return computed values through the following syntax (expressions within brackets are optional):

function [return-variable =] functionName([arg1, arg2, ...])  
{  
    // ... body  
}

A function-call is essentially inlined by the compiler, so it is not supported to call a function recursively. The compiler will report an error when a function appears more than once on the function-call-stack. In the example below, the “Hello World!” program from before is adapted to involve a function-call (without a return-value):

/* hellofunction.bfx */  
 
function main()  
{  
    hello("World");  
}  
 
function hello(who)  
{  
    prints "Hello ";  
    prints who;  
    prints "!\n";  
}

Comments

BrainFix supports two types of comments: end-of-line comments and C-style comments. EOL comments start at // and end at, of course, the end of the line. C-style comments are delimited by /* and */ respectively. All commented text will be ignored by the compiler.

Operators

Currently the language supports the following operators: =, +, -, *, /, % and their corresponding assignment-operators (e.g. +=). It also contains the common comparison operators <, >, ==, !=, <=, >= and logical AND (&&), OR (||) and NOT (!) to allow for more complex conditionals. Below is listed an example illustrating the use of the common arithmetical operators. The use of the conditional operators is shown in the next section (Flow Constructs).

/* arithmetic.bfx */  
 
function main()  
{  
    scan x; // read an integer value from stdin into the variable x  
    scan y; // same for y  
 
    z = 2 * (x + y) * (x % y); // compute the value and assign to z  
    printd z;   // print the decimal value of z  
    print ’\n’; // print a newline  
}

Flow Control

BrainFix supports flow control to a certain extent by implementing for-loops and if-else conditionals. The syntax of these constructs resembles MATLAB in the sense that no parentheses are required around if-conditions, and the range of the for is indicated using start:step:stop. The specification of a step value is optional and if omitted, it will be set to 1. The body of a for, if or else can contain only a single expression, or a compound statement between { and }.

/* flow.bfx */  
 
function main()  
{  
    // Get x and y from input  
    x = get("x");  
    y = get("y");  
 
    // Compare the two  
    compare(x, y);  
 
    // See if one or both were 0  
    zero(x, y);  
 
    // Print the alphabet  
    printSequence(’a’, ’z’);  
}  
 
function x = get(name)  
{  
    prints "enter ";  
    prints name;  
    prints ": ";  
    scan x;  
}  
 
function compare(x, y)  
{  
    more = "x is greater than y\n";  
    less = "x is less than y\n";  
    same = "x is equal to y\n";  
 
    if x < y  
        prints less;  
    else if x == y  
        prints same;  
    else if x > y  
        prints more;  
}  
 
function zero(x, y)  
{  
    if x == 0 && y == 0  
        prints "Both x and y are zero.\n";  
    else if x != 0 && y == 0  
        prints "x was not zero, but y was.\n";  
    else if x == 0 && y != 0  
        prints "y was not zero, but x was.\n";  
    else  
        prints "neither x nor y was zero.\n";  
}  
 
function printSequence(start, stop)  
{  
    for i = start:stop  
        print i;  
    print ’\n’;  
}

Arrays

As of version 0.32, the language supports arrays of which the size is known compile-time (statically allocated). There are two ways in which an array can be created: using the new array keyword, or by initializing a variable with an array denoted by a comma-seperated list between (square) brackets. Strings have been reimplemented and now behave exactly the same as arrays, meaning that they too can be indexed. A string literal, however, is guaranteed to have a terminating zero. The example below illustrates how arrays may be used:

/* arrays.bfx */  
 
function main()  
{  
    x = [0, 1, 2, 3, 4];  
    zeros1 = array 5;    // array of 5 zeros  
    zeros2 = array 5 0;  // the 0 at the end is optional  
    ones   = array 5 1;  // array of 5 ones  
 
    for i = 0:4  
    {  
        zeros1[i] = x[i];  
        printd zeros1[i];  
        print ’ ’;  
    }  
    print ’\n’;  
 
    str = "Hello World!\n";  
    str[1] = ’o’;  
    str[7] = ’e’;  
    prints str;  
}

Memory Management

A garbage collector collects unreferenced memory and makes it available for other purposes. Old variables can safely be overwritten and reused. Because each function has its own scope, variables having the same name will not cause nameclashes across function scopes. When parameters are passed between functions, they will be passed by value. That is, the function will receive a copy of the original variable, even if it is a string or an array.

Compilation

Compiling BrainFix into BrainFuck using the bfx compiler is a single step procedure, but unless you have a machine that can execute BrainFuck instructions directly, you will need another tool to translate the resulting BrainFuck code to C (or any other mainstream language). I have included my own little translator, called bf2c, to do this work. I recommend you use this one, even though it does not optimize and is very primitive in all respects. The reason I still recommend this is because it implements some minor subtleties:

An array of integers is used to enable computations with numbers that exceed 1 byte. When reading from the input, a decimal value is read instead of a character. Before decrementing a value, it is first checked if this value is already 0. If so, no action is performed. Interpreters that do not implement this behavior will probably fail at producing a working program. To compile your BrainFix progam, simply run1:

$./bfx file1.bfx file2.bfx ... filen.bfx file.bf

This will produce a BrainFuck source-file file.bf, that can be translated to C by bf2c:

$./bf2c file.bf file.c

The final step before running the code is to compile the C-source by a compiler of your choice (e.g., gcc):

$gcc -o program file.c  
$./program

Implementation Details

Parsing the input file(s)

To parse the input, two parsers were used. Each parser has its own lexical scanner to collect the tokens and was generated by Flexc++. The parsers themself were generated by the Bisonc++ parser generator. The first parser (Preprocessor::Parser) does not parse the actual bodies of each function, but instead it collects all functions and stores their body internally in a std::map<std::string,></std::string,>, using the function-name as the map-key. The second parser Compiler::Parser) then starts by asking the preprocessor for the main body, reporting an error when this does not exist. A function call is recognized by an identifier, followed immediately by an opening parenthesis. When this happens, the parser initializes a new parser on the stack, which will parse the body of this function. This is also why recursive calls are forbidden: they will result in an infinite stack of parsers. Therefore, when a parser is initialized, it stores the function-name in a static std::vector<std::string></std::string> which can be used to detect recursiveness: it is forbidden to call a function that was already stored in the vector. When, eventually, the parser returns, it dies automatically (it was allocated on the stack), and the mother- parser continues parsing as if nothing ever happened. The called function has effectively be inlined. I see no other way to compile function calls to BrainFuck other than inlining them. The grammar specification files used to generate these scanners and parsers are included in the package. I will not discuss these here, but if you have any questions regarding these specification files, please do not hesitate to contact me!

Class Hierarchy

The class hierarchy of bfx is shown in the figure below. Each of the classes has been generated by Bisonc++ (parsers) or Flexc++ (scanners). In the coming sections, I will discuss algorithms that are called through function-calls, e.g. assign(). These functions are members of the Compiler::Parser class.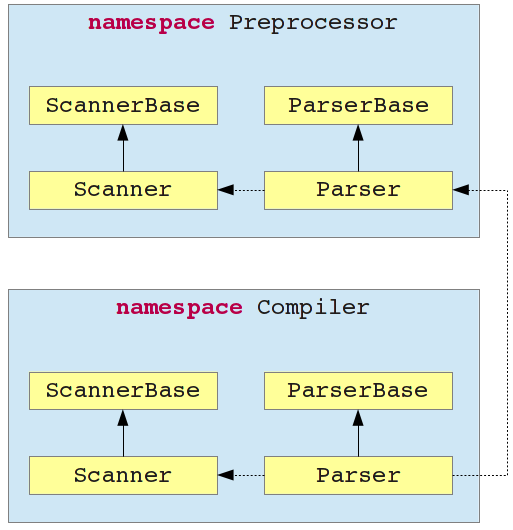

Memory Management

At no point during compilation will the compiler have any clue as to what the value of any of the memory cells will be at runtime. Only the addresses of each variable are registred internally in a std::vector<std::string></std::string>. I am aware that this severely limits the performance, as optimizing constant expressions will dramatically reduce the resulting BF code. However, I chose not to implement constant expressions (evaluated by the compiler), because this would complicate the parser too much. It might be something for the future but let’s be honest: BrainFuck was never designed to be compact. Allocation of memory happens by assigning a string to an element of the vector. Elements that have empty strings are considered to be available for allocation of variables, arrays and temporaries. In the case of a variable, the identifier (as specified by the programmer) is stored. Temporary variables (allocated by the compiler) are given an identifier __temp__ to enable the garbage collector to easily identify temporaries and clear these from memory. Memorycells that are part of an array, and are thereby refered to by a pointer that lives somewhere else, are tagged as __refd__ . Memorycells that are temporary, but need to survive on the stack until the end of the scope of an if- or for-construct are tagged with __stack__ . These variables are cleared when popStack() is called.

Variables

When the parser encounters a variable, it calls the function Compiler::Parser::allocate(std::string), where the argument matches the name of the variable (the identifier). This function then checks whether this variable already exists and if not, it will find some free memory for it to store it in. The address of the variable is returned in both cases, and this behavior is characteristic for almost every function the parser will call.

Constants

A constant is treated like any variable by the compiler, except that its value is stored in a memory location that is tagged by __temp__ , in order for it to be freed as soon as the delimiting semicolon is encountered. In the mean time, the value can be used for calculation without the end-user ever knowing that it was even stored somewhere.

Arrays and Strings

 

When multiple memory-cells have to be allocated to store a string or an array, the identifier is stored in a single cell, and a seperate array of empty cells is allocated elsewhere and tagged with __refd__ to indicate that this memory should be refered to by another variable. To keep track of which variables are pointers, the compiler stores them in a std::map<int,>></int,>. The key is the memory location of the pointer, and the pair of ints holds both the start of the array and the number of elements associated with it. In addition, another map is used to store only the array-addresses and the number of elements associated with them. This map is superfluous, since this information is already contained in the map discussed before, but it simplifies the algorithms used for garbage-collection.

Garbage Collection

When the terminating semicolon is encountered, all temporary variables may be freed. The memory they occupy can be reused in the next expression. This means that the vector is searched for entries containing __temp__, which are then cleared. When the temporary variable happens to be a pointer, it is also removed from the map of pointers. When all temporary variables have been freed, unreferenced memory (tagged with __refd__) is located and freed as well.

Assignment and Arithmetic

Each operation (recognized by the parser), results in a function-call that generates BF- code. This section will give some examples and BF algorithms to clarify this process. To do so, I will use <expr></expr> to indicate an expression. An expression can be anything from a single variable or constant, to a complex assembly of variables, constants and operators.

Assignment

An assignment is of the form <expr> = <expr> ’;’ , for which the compiler knows where the values of each of the expressions are stored in memory. We now need to copy the value of the right-hand-side (rhs) to the address of the left-hand-side (lhs). When these two addresses are adjecent, one would do this using the following BF algorithm (assuming the pointer points to the rhs-element, and copies this value one cell to the right):

Memory contents:
| rhs (x) | lhs (y) | tmp (z) |
    * (pointer)

>[-]>[-]<<    // CLEAR the lhs cell and tmp cell
[->+>+<<]     // MOVE the value in rhs to both lhs and tmp
>>[-<<+>>]    // MOVE the value back to rhs

| rhs (x) | lhs (x) | tmp (0) |

Of course, the available memory cells will in practise not always be adjecent. They might be very far apart, and the direction of travel may vary as well. Luckily, because the compiler knows where each variable is stored, this can be easily calculated by the member Compiler::Parser::movePtr(idx), which will generate code to move the pointer to the desired index. However this requires that the compiler keeps track of the current index, which is stored in a (static) data member. Using this member, the algorithm transforms to:

Function call: assign(lhs, rhs)

movePtr(lhs) [-]
movePtr(tmp) [-]
movePtr(rhs)
[-
  movePtr(lhs)
  +
  movePtr(tmp)
  +
  movePtr(rhs)
]

movePtr(tmp)
[-
  movePtr(rhs)
  +
  movePtr(tmp)
]

Addition

For each of the arithmetic operators, an assignment variant is implemented which directly modifies its left-hand operand (e.g. x += 5 will add 5 to x). The regular operators can then easily be implemented in terms of their assignment variants.

<expr> ’+=’ <expr>
Function call: addTo(lhs, rhs)
Memory: | lhs | rhs | tmp |
           *

assign(tmp, rhs) // make a copy of rhs and store it in the temporary
>>[-<<+>>]       // add the value in tmp to the value in lhs

The regular addition returns a temporary variable holding the sum of both operands, making use of the addTo() algorithm above.

<expr> ’+’ <expr>
Function call: add(lhs, rhs)
Memory: | lhs | rhs | tmp |

assign(tmp, lhs) // store a copy of the lhs in tmp
addTo(tmp, rhs)  // add the rhs to this temporary
return tmp       // return the result

Subtraction

The subtraction algorithm is trivially derived from the addition algorithms by replacing the + by a minus sign (-). In principle it is possible to implement negative numbers, but a lot of my implementations depend on letting a cell decrease to 0 using [- ...]. When a number is already negative, this would result in an infinite loop. Therefore, I assume that the program that translates the resulting BF code to C (or some other language) implements a check before decrementing the cell, i.e. if (*ptr) --*ptr;. The resulting algorithms can be called through subtractFrom() (-=) and subtract() (-) respectively.

Multiplication

Multiplication is implemented through repeated addition. To multiply a value by another value, we just keep adding this value to itself while decrementing the other, until it reaches zero. The algorithm becomes:

<expr> ’*=’ <expr>
Function call: multiplyBy(lhs, rhs)
Memory: | lhs | rhs | tmp1 | tmp2|

assign(tmp1, lhs)
assign(tmp2, rhs)
movePtr(lhs)
[-]                  // set the lhs to 0
movePtr(tmp2)
[-                   // keep decrementing tmp2
  addTo(rhs, tmp1)     // while adding tmp1 to rhs
  movePtr(tmp2)        // and move back to tmp2
]

The regular multiplication (returing a temporary) is exactly like the one we saw before in the addition example, after substituting the addTo() call by multiplyBy(). I will omit these implementations from now on.

Division

The division algorithm uses both the subtraction and multiplication algorithms previously described. It starts by subtracting the denominator from the numerator until it becomes 0, while counting how many times this could be done. For example, when calculating 24/7, we would find that we can subtract 7 4 times from 24 before we reach zero. However, since we’re doing integer division, we would like the result to be rounded down rather than up, so we derive the remainder by subtracting the numerator (24) from the product of the denominator and the counter (rem == 4 * 7 - 24). When the remainder turns out to be nonzero, the counter is decremented to obtain the floored result. To check whether a variable is nonzero, we initialize a temporary flag to 0, which will be set to 1 inside a conditional statement. This flag is then subtracted from the counter to require the desired result:

<expr> ’/=’ <expr>
Function call: divideBy(lhs, rhs)
Memory: | lhs | rhs | cpy | cnt | rem | flag |

assign(cpy, lhs)         // make a copy of the left hand side
movePtr(cpy)
[
  subtractFrom(cpy, rhs)   // keep subtracting the right hand side from this copy
  movePtr(cnt)             // while counting how many times this can be done
  +
  movePtr(cpy)
]

rem = multiply(cnt, rhs) // calculate the product
subtractFrom(rem, lhs)   // and subtract the left-hand side to obtain the remainder
movePtr(rem)
[[-]                     // only if the remainder was nonzero will this loop be entered
  movePtr(flag)
  [-]+                     // set the flag to 1
  movePtr(rem)             // rem is now 0 so the loop is broken
]                        

subtractFrom(div, flag)  // subtract 1 from the answer when the remainder was nonzero
assignTo(lhs, div)       // update the left-hand-side

Modulo

The modulo operation is implemented entirely in terms of existing algorithms. It might not be the most efficient algorithm, but it is easy to implement:

<expr> ’%=’ <expr>
Function call: moduloBy(lhs, rhs)
Memory: | lhs | rhs | tmp |

assign(tmp, lhs)
divideBy(tmp, rhs)
subtractFrom(lhs, multiply(tmp, rhs))

Comparisons and Logicals

Comparisons are an important feature in programming languages that support conditional constructs. Therefore, BrainFix supports the well known logical operators (&&, ||) as well as the comparison operators (<, >, <=, >=, ==, !=).

Less Than: <

To check whether one expression is less than another, we let each of them go to 0. The condition is broken when the left-hand-side actually reaches zero. In the case that that the left-hand-side was actually smaller than the right-hand-side, the latter will not yet be zero when the loop is broken. This can be checked using the flag-approach we have already seen in the division-implementation.

<expr> ’<’ <expr>
Function call: lt(lhs, rhs)
Memory: | lhs | rhs | tmp1 | tmp2 | ret |

assign(tmp1, lhs)   // copy both sides to temporaries
assign(tmp2, rhs)

movePtr(tmp1)
[-                  // keep decrementing the lhs
  movePtr(tmp2)     // while also decrementing the rhs
  -                   
  movePtr(tmp1)     // quit the loop when the lhs is 0
]

movePtr(tmp2)       // if the rhs is still nonzero, it was larger
[[-]
  movePtr(ret)
  [-]+              // and ret becomes 1 (otherwise remains 0)
  movePtr(tmp2)
]

Greater Than (>)

The greater-than sign is implemented just like the less-than operation. The only difference is that this time, we quit the loop when the right-hand-side reaches zero and use the remainder of the left-hand-side to set the flag. The resulting call is gt(lhs, rhs).

(In)equality: (==, !=)

The equality check can be implemented in terms of the inequality checks that were discussed in the preceding sections: two expressions are equal if the first is neither greater nor less than the other. We can thus use the outcomes of these operators to set a flag when either of both is true. Keep in mind that if this flag is set, this means that they are not equal, so we subtract the flag from 1 to obtain the final result.

<expr> ’==’ <expr>
Function call: eq(lhs, rhs)
Memory: | lhs | rhs | less | more | flag | ret |

less = lt(lhs, rhs)
more = gt(lhs, rhs)
movePtr(less)             // check if lhs < rhs
[[-]
  movePtr(flag)
  [-]+
  movePtr(less)
]

movePtr(more)             // check if lhs > rhs
[[-]
  movePtr(flag)
  [-]+
  movePtr(more)
]

movePtr(ret)
[-]+                      // set ret to 1
subtractFrom(ret, flag)   // and subtract the flag

The implementation of the inequality operator is identical to that of the equality operator, except that the result (flag) does not have to be inversed.

Less than/Greater than or equal (<=, >=)

The principle we saw in the previous section can be used again to implement the less/equal and greater/equal operators. The only difference this time is that we can directly use the flag as the return value. I will give the implementation of the less/equal operator and omit its counterpart, which is analogous to the following:

<expr> ’<=’ <expr>
Function call: le(lhs, rhs)
Memory: | lhs | rhs | less | same | ret |

less = lt(lhs, rhs)
same = eq(lhs, rhs)

movePtr(less)
[[-]
  movePtr(ret)    // check if lhs < rhs
  [-]+
  movePtr(less)
]

movePtr(same)     // check if lhs == rhs
[[-]
  movePtr(ret)
  [-]+
  movePtr(same)
]

Logical AND (&&)

The logical operators (not bitwise!) can be combined with any of the comparison operators to for complex conditionals. Their implementation again relies on setting flags and combining these flags to get the desired result. For the logical AND, the BF implementation is as follows:

<expr> ’&&’ <expr>
Function call: logicAnd(lhs, rhs)
Memory: | lhs | rhs | cpy1 | cpy2 | flag1 | flag2 |

assign(cpy1, lhs)          // copy both operands
assign(cpy2, rhs)

movePtr(cpy1)              // see if the lhs is nonzero
[[-]
  movePtr(flag1)
  [-]+
  movePtr(cpy1)
]

movePtr(cpy2)              // see if the rhs is nonzero
[[-]
  movePtr(flag2)
  [-]+
  movePtr(cpy2)
]

multiplyBy(flag1, flag2)   // multiply the flags

// flag1 == 1 if and only if both lhs and rhs were nonzero

Logical OR (||)

The logical OR is similar to the AND operator, but it adds the two flags instead of multiplying them. This however could result in a value other than 0 or 1, so a third algorithm is used to get the final result.

<expr> ’||’ <expr>
Function call: logicOr(lhs, rhs)
Memory: | lhs | rhs | cpy1 | cpy2 | flag1 | flag2 | ret |

assign(cpy1, lhs)                  // copy the operands
assign(cpy2, rhs)

movePtr(cpy1)                      // see if the lhs is nonzero
[[-]
  movePtr(flag1)
  [-]+
  movePtr(cpy1)
]

movePtr(cpy2)                      // see if the rhs is nonzero
[[-]
  movePtr(flag2)
  [-]+
  movePtr(cpy2)
]

addTo(flag1, flag2)                // add them together

movePtr(flag1)
[[-]
  movePtr(ret)                     // ret becomes 1 if flag1 != 0
  [-]+
  movePtr(flag1)
]

Logical NOT (!)

The logical NOT operator was already used implicitly in the implementation of the equality-check algorithm, where we needed to subtract the flag from 1 to obtain the inversed result. The algorithm is:

’!’ <expr>
Function call: logicNot(rhs)
Memory: | rhs | cpy | flag | ret |

assign(cpy, rhs)          // copy the operand
movePtr(cpy)
[[-]
  movePtr(flag)   
  [-]+                    // flag becomes 1 if rhs != 0
  movePtr(cpy)
]

movePtr(ret)
[-]+                      // set the return value to 1
subtractFrom(ret,flag)    // and subtract the flag

Flow

The BrainFix language supports only a few flow-control structures: if(-else) and for. This is sufficient to write complex programs, therefore I chose not to go through the trouble of implementing the more difficult while or switch statements. In future releases of this program, it might still become a feature and if you feel the urge to contribute, I will greatly appreciate it!

if-else

To implement the if conditional with an optional else clause, we must provide the compiler with yet again some extra members. The problem is that conditional expressions can only be realized in BF by using the square brackets, which means that at the closing bracket, the pointer must be at a cell from which we know it to be zero. We could do this by just creating a temporary variable which is set to zero, but this would be a waste of memory. Instead, the address of the expression that acts as the conditional (ifFlag) is stored on a std::stack<std::vector<int>></std::vector<int>, together with the inverse of this conditional (elFlag). A stack is the most natural container in this case, because it enables nested if’s without further effort. When the parser encounters the end of the if-body, it can just move the pointer to the ifFlag (which has been set to 0) and terminate the loop after only ‘looping’ once. When an else clause is appended by the programmer, the compiler will move the pointer to the location of the elFlag. To ensure that the memory occupied by these flags is not freed until the end of the scope of the if-else, their cells are tagged with __stack. A special function is dedicated to freeing the memory associated with the topmost elements of the stack: popStack(). This function is called by the parser when it encounters the final closing brace of an if-else construction.

The following example illustrates what happens if the parser encounters an if-else statement:

if x < 10 && y > 10   // push (ifFlag, elFlag) on the stack
{                     // movePtr(ifFlag) [-
    // body           // parse body as usual
}                     // ]
else                  // movePtr(elFlag)
{                     // [-
    // body           // parse body as usual
}                     // ] popStack()

for

I chose to mimic the MATLAB-syntax of the for-loop, because of its clarity and simplicity. It is also easier to implement than the C-syntax, because the C-syntax requires a conditional to be checked over and over again. In contrast, the MATLAB-syntax forces the programmer to provide the compiler with the startcondition, stopcondition and stepsize, each of which can be pushed on to the stack as we saw in the previous section. This is what happens at a for statement:

for x = start:step:stop  // start is assigned to x and the addresses of
                            x, step and stop are pushed on the stack. A
                            fourth cell, named flag, is created by calling
                            le(x, stop) to determine if the loop needs to
                            be executed. Start loop: movePtr(flag) [
{
    // body              // parse body as usual
}                        // x, step, and stop are fetched from the stack
                            and step is added to x. The flag is updated
                            by calling le(x, stop) again, and the loop is
                            closed: movePtr(flag) ] popStack()

Arrays

Implementing arrays proved to be a challenge because I wanted the programmer to be able to index these arrays using variables of which the value is not known compile-time, e.g. scan i; arr[i] = 1;. The reason for this to be a challenge, is that the pointer has to be moved to a memory-cell of which the compiler cannot know the address. I needed to come up with an algorithm that could move to the desired cell, do some operations on that cell, and move back to some known location. The last step (moving back) is crucial because the compiler must always know what the pointer is pointing to.

Fetching a Value

Function call: arrayValue(array, index)

When the element needs not to be modified (i.e. it is used as an r-value), it is sufficient to copy the element to some known location. The copy can then be used to do further computations with (e.g. y = 3 * x[i]). In order to do so, a maximum array size is set to 256 elements (MAX ARRAY SIZE), and a buffer (buf) of this size is allocated.

Within this buffer, we can move an unknown number of cells (i) to the right by first copying i to both the first (buf[0]) and second cell (buf[1]) and then applying the following algorithm (assuming the pointer initially points to buf[0]):

[>[->+<]<[->+<]>-]

This algorithm essentially pushes the second cell forward while decrementing the first cell, causing the pointer to be shifted by an amount i.

Now, because we know the distance between (the start of) the buffer and the actual array, we can translate the pointer back to the array itself, where it will end up precisely at the required element. We can now apply a copy-algorithm to copy the value to the buffer and move the pointer (together with the copy) back the same amount using the value we left behind in the last cell.

When the algorithm is completed, we can clear the rest of the buffer (excluding the first element) before returning the address of the first address.

Assignment

Function call: assignToElement(array, index, value)

The same tactic is used to assign a value to an element of an array, but this time the value to be assigned is moved (pushed forward by an amount i) in the buffer as well. The situation would be like that in the figure above, with an additional cell containing the value to be assigned. The usual assignment algorithm can be employed to change the cell in the array, and the pointer can move back to the start of the buffer.

Arithmetic

Applying arithmetical operations to array-elements is easy now we have the tools to fetch values (arrayValue()) and assign values (assignToElement()). Each of the arithmetic algorithms has the same structure:

1. Get a copy of the element (arrayValue())

2. Apply the operation (add, subtract, etc.)

3. Store the result in the array (assignToElement())

Contact 

Feel free to contact me to report bugs, or express your feelings (about this piece of software).