Introduction
The interest of building a PC parser (predicate calculus) has been always puzzling me. Ever since the time I was first introduced to the
simplicity of deductive reasoning in the early 90s, I have always wanted to create a parser for the rules which to be named as my PC parser. Here I
describe why, an how of this step as we see English sentences, logics, and computer reasoning as one in our attempt to build such a mechanism.
To understand the relationship of logic reasoning and English language, we need to see the grammatical rules of English language; and how a predicate
calculus can be constructed on it. Logical reasoning, especially deductive logic in the computational form of the predicate calculus (propositional
calculus) is established as such that: all the predicates (sentences) form the basis of the reasoning and the foundation of the knowledge closure; and we test
our conclusion (a test sentence) through the traversal of these predicate sentences which have been parsed using set of PC rules.
A simple English sentence may be: Tom loves Lucy where Tom is the subject, “love” is the action, and Lucy is the object. And in C#, we parse each
English sentence using pattern matching in regular expressions.
An Abstract Attempt
Below I have randomly written some outrageous pattern matching schemes that in a way to promote a simple way to confine our search to a set of very simple grammatical sentences.
A simple sentence pattern may be:
((a|the)
)?(\w)+ (am|is|was|were|are|had been|have been) ((a|the) )?(\w)+
E.g.
A dog is a friend
Dogs are friends
Doug is a friend
Doug is furious
An prepositional sentence pattern has relationship of subject and
object with object prepositions such as “after, around, from, ….”
((a|the) )?(\w)+
(am|is|was|were|are|had been|have been) (\w)+ (after|in|from|around|at|about)
((a|the) )?(\w)+
Where word after “be” is an adverb, a verb in
continuous form, or in the past tense describing the action is done as with the
“be” to form an adverb describing the subject.
E.g.
Doug is furious
about the situation
Therefore we can define a conjugational sentence with preposition can
be:
Tom is furious
about love, money, and power.
Tom is both a
romantic lover and a greedy merchant
Chris was angry
and Lucy lost her patience
He can only choose
either to hate or to ignore it.
And its pattern
((a|the|an) )?(\w+) (is|was|am|are|were|had been|have
been|has been) (\w+) (after|in|from|around|at|about) (a |the )?(\w+,
)+(\w+)(,)? (and|or) (\w+)
<o:p>
For a sentence should have either an implicit timeline or a detailed
explicit timeline.
So we can say:
Tom has been very anxious in the past. (S1)
Or we can say:
Tom has been very
anxious in the past two weeks.
An implicit timeline covers the following timely terms in some vague
sense:
Long ago, past, recently, now, later, tomorrow, in a
few days, in the future.
So (S1) includes time period from Long ago -> now. Given no other
predicate conditions, we can then draw
conclusion:
Tom still feels
anxious right now.
The design requirement of a reasonable logical sentence parser should at
least draw a subset of the grammatical logical structure of a discipline of the
English grammar. In a discipline we mean that we don’t want to say whatever,
but follow a set of rules of expression in the writing of our reasoning. So to
form a list of logical predicate sentences as a closure to our conclusion, we call
this clearly as the propositions. And the propositions must be true and can
directly lead to our presumption or we say our test string in order for the
predicate test to be true. So our job is to conclusively test the supplied test
sentence whether it should return a Boolean value of True or False, or
otherwise uncertain (value of Null) from the test as the propositions are not
enough for the conclusion to be drawn.
So we start by list out our propositions in a list we call the
PropositionList -> typed List<string>.
This list is a class that uses a List<string> to store sentences.
First of all, we gather all of the sentence to form our little universe in the
list. Then we parse all the sentences, first is to ensure they are in
grammatical forms that fit to our set of rules by pattern matching of the
sentences using regular expressions. This also defines the sentence types may
it in the PC (Predicate Calculus) been defined as simple (subject verb object),
compound (conjugations) or conditional (if and iff) for example.
For simplicity we like to begin with a most reasonably simple
discipline (grammatical rules) of our logical construct. By examples, so we
like to same in the most simple and elegant manner of the following :
- Tom is late
(simple
adverb predicate)
- Tom shoots a gun (simple action predicate)
- Chris loves Lucy but Lucy hates Chris (this is a
simple conjunction of AND operator)
- Chris loves gun and rose (this can be separated
into two simple predicate)
- Chris knows neither Tom nor Nancy (another simple
conjugation)
These simple rules would allow us to interact with a small set of
grammatical sentences to which we accept as our language. And we need to keep a
dictionary of action words (or verbs) in all the tenses. In the real world PC
implementation we should have the complete dictionary as reference.
So we like to define the following (most simple):
Sentence =
SimpleSentence | CompoundSentence | ConditionalSentence
SimpleSentence =
Subject Action Object
CompoundSentence =
SimpleSentence and|or SimpleSentence
ConditionalSentence
= IF SimpleSentence THEN SimpleSentence
Then we parse our sentences in a loop which also produce a term(symbol)
table lookup. And we have a predicate list which sort of like the following:
T loves L
L loves T | L
loves C
If not (A loves B)
then A hates B
L hates C
And in the symbol lookup we have accumulate the following T = Tom, L =
Lucy, and C = Chris. And we supply our test sentence: L loves T? And our nice
predicate parser will parse all of them, so the conclusion is true. On the
other hand, if we test: L Hates T; we will have a unresolved condition at 2nd
sentence, so the conclusion would be false.
Another approach to implement this simple logical grammar parser (or of
PC – predicate logic reasoning), we will take a look at the graphical
presentation and interpretation of nodes by traversal to derive or similarly to
parse the conclusion.
Using Subject and Object as nodes: these include both nouns and adverbs
of describing conditions; and also using BE (is, am, are, etc.) and action verbs
are pointers we can describe our closed universe as a labeled graph.
The flowing is our little list of propositions (predicates):
- Tom loves Lucy
- Chris loves Lucy but Lucy hates Chris
- Lucy loves either Tom or Chris (Lucy must love
one, we know it for sure!)
So we want to parse our conclusion that Lucy loves Tom. And first we
need to quickly construct our little graphical presentation by parsing the
nodes… And the result is as follows:
Our dictionary of terms:
Tom T
Lucy L
Chris C
We need to draw a minimum set of disjoint graphs.
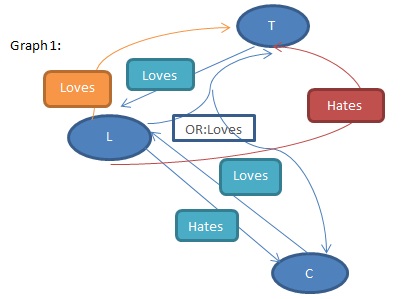
So in the graph, the strait blue pointers represent direct connection
of two nodes with action label. And the curved separator represents a OR
condition with labeled action. Up to here we do need some more details in our
dictionary – we probably need a thesaurus to tell us what words are similar or
opposite, so we can tell that “love” and “hate” are opposite each other. And our conclusive test sentence: Does Lucy
Love Tom? We draw the test pointer in yellow…
So we go from node ‘L’, and we see that ‘L’ can either ‘Love’ Tom or
‘Love’ Chris; and ‘L’ Hate Chris. But can the yellow pointer be legal? From
here we test all joint edges (or arcs) to see if they are legal. This should be
a O(n) algorithm since we test each edge only once. But if we are to test Lucy Hates Tom –
presented in the red curved arrow, we shouldn’t be parsing all edges legally.
Because from here we will have these a contradiction: L (hate)-> T(e1); T
(love)-> L(e2); L either(love)->T or(love)->C(e3); (but e1 invalidates
L(hate)->C(e4). So this parse draws false conclusion for the test sentence.
And we also know by thesaurus and negation (PC) that Lucy Hates Tom is false
means Lucy Loves Tom is true. So both parses draw the same conclusion.
Using graphical presentation to solve logical reasoning may refer to
this method can be called a semantic network – because it solves with records
of knowledge.
In comparison of the two methods in the solving of simple logical
reasoning, we are comparing the compiling of objects in the parser project or
the depth, scope and simplicity of the semantic network. Both are competing methods
for the PC (predicate calculus). And both methodologies are important. Ina
regular scope, we definitely need a complete parser in future for the English
Language – which links dictionary, thesaurus, and translators will have a
universal impact. On the foundation of such, we explore the simplicity of the
semantic network so that extremely complicated reasoning can be construct and
evaluated in a compiling fashion that pushes AI reasoning simulation and AI
consultation schemes on the fly. As we build up our blocks of knowledge and
computation of the AI, we draw our attention onto the applications of which –
these conclusively are in the domain of semantic networks.
