Introduction
I am a geocacher and one weekend in January 2012, we went to Heidelberg and while there a new geocache was published where one had to solve a formula based Sudoku puzzle. A group of us solved it manually (in about 30 minutes). Once back at work, I showed a work collogue (let's call him Bob) the puzzle and we started chatting if it would be possible to write a LINQ query to solve this puzzle.
Bob showed me the MSDN blog article, Using LINQ to solve puzzles and we used this as a basis to solve this Sudoku puzzle.
The original article was published by me on 25th of January 2013 here.
Background
This is what the formula based Sudoku puzzle looks like:
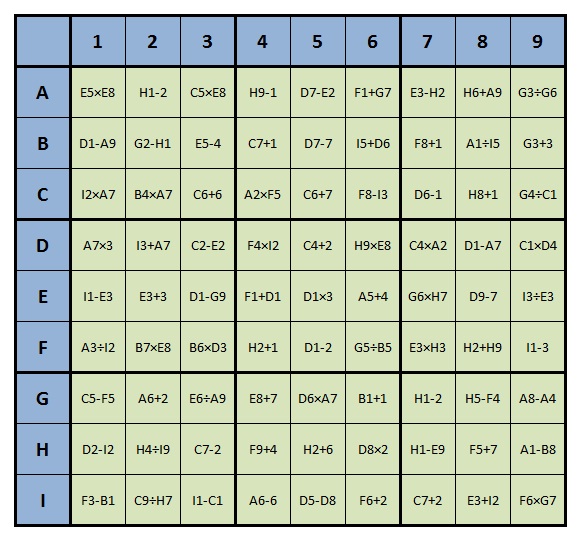
First, I wanted to understand how this LINQ query would work by simplifying the problem.
Proof of Concept
I drew a small 3 by 3 grid and entered some numbers.

I entered "random" numbers from 1 to 9 into each cell. At this stage, I am simulating one section of the Sudoku puzzle, so that when I write the LINQ query I can understand it better. It is much simpler to work with a 3x3 grid and understand what is going on than working with a 9x9 grid.
Once I had the numbers, then I made up some of my own formulas as follows:

As it happened, I did enter three circular references. This helped me understand how the "from" and "joins" work later on (see further below).
I started with the brute force method as per the MSDN blog, and the code I started off with looked like this:
var solveForNumbers =
from a1 in Enumerable.Range(1, 9)
from a2 in Enumerable.Range(1, 9)
from a3 in Enumerable.Range(1, 9)
from b1 in Enumerable.Range(1, 9)
from b2 in Enumerable.Range(1, 9)
from b3 in Enumerable.Range(1, 9)
from c1 in Enumerable.Range(1, 9)
from c2 in Enumerable.Range(1, 9)
from c3 in Enumerable.Range(1, 9)
where (a1 == b3 - 4)
&& (a2 == a3 - b2)
&& (a3 == b2 * c3)
&& (b1 == a3 + a1)
&& (b2 == c2 - a3)
&& (b3 == a1 + a2)
&& (c1 == a3 + c3)
&& (c2 == a2 * b2)
&& (c3 == b3 - b2)
select new
{ a1, a2, a3, b1, b2, b3, c1, c2, c3};
Solving this basic puzzle took around 110 seconds on my laptop. For the big puzzle (9 x 9 grid) to be solved this way would take exponentially longer.
I then started, as per the MSDN blog post, to move each "where" clause into a "join". I wanted to see the speed improvements along the way.
I moved the 1st entry "c3" into a join as follows:
var solveForNumbers1 =
from a1 in Enumerable.Range(1, 9)
from a2 in Enumerable.Range(1, 9)
from a3 in Enumerable.Range(1, 9)
from b1 in Enumerable.Range(1, 9)
from b2 in Enumerable.Range(1, 9)
from b3 in Enumerable.Range(1, 9)
from c1 in Enumerable.Range(1, 9)
from c2 in Enumerable.Range(1, 9)
join c3 in Enumerable.Range(1, 9) on b3 - b2 equals c3
where (a1 == b3 - 4)
&& (a2 == a3 - b2)
&& (a3 == b2 * c3)
&& (b1 == a3 + a1)
&& (b2 == c2 - a3)
&& (b3 == a1 + a2)
&& (c1 == a3 + c3)
&& (c2 == a2 * b2)
select new
{ a1, a2, a3, b1, b2, b3, c1, c2, c3};
I reran the test and now it took only 12 seconds. Wow! That is a saving of almost 100 seconds.
With some help from Rankadu, I moved them all across and ended up with this code:
var solveForNumbers1 =
from b2 in Enumerable.Range(1, 9)
from a3 in Enumerable.Range(1, 9)
from a1 in Enumerable.Range(1, 9)
join a2 in Enumerable.Range(1, 9) on a3 - b2 equals a2
join b3 in Enumerable.Range(1, 9) on a1 + a2 equals b3
join c3 in Enumerable.Range(1, 9) on b3 - b2 equals c3
join c2 in Enumerable.Range(1, 9) on a2 * b2 equals c2
join b1 in Enumerable.Range(1, 9) on a3 + a1 equals b1
join c1 in Enumerable.Range(1, 9) on a3 + c3 equals c1
where (b2 == c2 - a3)
&& (a3 == b2 * c3)
&& (a1 == b3 - 4)
select new
{ a1, a2, a3, b1, b2, b3, c1, c2, c3};
Some explanation is required here:
The reason b2, a3, and a1 are left in the "from" portion is that there is a circular reference to that value.

- b2 == c2 - a3
- and c2 == a2 * b2
- and a2 == a3 - b2
- (b2 depends on c2, and c2 depends on b2)
- (b2 depends on c2, and c2 has a2, and a2 depends on b2)
So there is no reliable way for the "join" to know what the value is therefore it must be left in the from section of the code.
The Ordering of the Joins

When a join is added, the values of the formula must already be known at the time (previously defined). Since c3 == b3 - b2, the value b3 and b2 must be defined before the c3 join.
Once I had this in place and the tests running, I now knew how to solve the 9x9 grid.
Using the Code
While I was testing the proof of concept on the 3x3 grid Bob got going with the 9x9 grid brute force (or "where clause" method).
This is the result:
var solveForNumbers =
from a1 in Enumerable.Range(1, 9)
from a2 in Enumerable.Range(1, 9)
from a3 in Enumerable.Range(1, 9)
from a4 in Enumerable.Range(1, 9)
from a5 in Enumerable.Range(1, 9)
from a6 in Enumerable.Range(1, 9)
from a7 in Enumerable.Range(1, 9)
from a8 in Enumerable.Range(1, 9)
from a9 in Enumerable.Range(1, 9)
from b1 in Enumerable.Range(1, 9)
from b2 in Enumerable.Range(1, 9)
from b3 in Enumerable.Range(1, 9)
from b4 in Enumerable.Range(1, 9)
from b5 in Enumerable.Range(1, 9)
from b6 in Enumerable.Range(1, 9)
from b7 in Enumerable.Range(1, 9)
from b8 in Enumerable.Range(1, 9)
from b9 in Enumerable.Range(1, 9)
from c1 in Enumerable.Range(1, 9)
from c2 in Enumerable.Range(1, 9)
from c3 in Enumerable.Range(1, 9)
from c4 in Enumerable.Range(1, 9)
from c5 in Enumerable.Range(1, 9)
from c6 in Enumerable.Range(1, 9)
from c7 in Enumerable.Range(1, 9)
from c8 in Enumerable.Range(1, 9)
from c9 in Enumerable.Range(1, 9)
from d1 in Enumerable.Range(1, 9)
from d2 in Enumerable.Range(1, 9)
from d3 in Enumerable.Range(1, 9)
from d4 in Enumerable.Range(1, 9)
from d5 in Enumerable.Range(1, 9)
from d6 in Enumerable.Range(1, 9)
from d7 in Enumerable.Range(1, 9)
from d8 in Enumerable.Range(1, 9)
from d9 in Enumerable.Range(1, 9)
from e1 in Enumerable.Range(1, 9)
from e2 in Enumerable.Range(1, 9)
from e3 in Enumerable.Range(1, 9)
from e4 in Enumerable.Range(1, 9)
from e5 in Enumerable.Range(1, 9)
from e6 in Enumerable.Range(1, 9)
from e7 in Enumerable.Range(1, 9)
from e8 in Enumerable.Range(1, 9)
from e9 in Enumerable.Range(1, 9)
from f1 in Enumerable.Range(1, 9)
from f2 in Enumerable.Range(1, 9)
from f3 in Enumerable.Range(1, 9)
from f4 in Enumerable.Range(1, 9)
from f5 in Enumerable.Range(1, 9)
from f6 in Enumerable.Range(1, 9)
from f7 in Enumerable.Range(1, 9)
from f8 in Enumerable.Range(1, 9)
from f9 in Enumerable.Range(1, 9)
from g1 in Enumerable.Range(1, 9)
from g2 in Enumerable.Range(1, 9)
from g3 in Enumerable.Range(1, 9)
from g4 in Enumerable.Range(1, 9)
from g5 in Enumerable.Range(1, 9)
from g6 in Enumerable.Range(1, 9)
from g7 in Enumerable.Range(1, 9)
from g8 in Enumerable.Range(1, 9)
from g9 in Enumerable.Range(1, 9)
from h1 in Enumerable.Range(1, 9)
from h2 in Enumerable.Range(1, 9)
from h3 in Enumerable.Range(1, 9)
from h4 in Enumerable.Range(1, 9)
from h5 in Enumerable.Range(1, 9)
from h6 in Enumerable.Range(1, 9)
from h7 in Enumerable.Range(1, 9)
from h8 in Enumerable.Range(1, 9)
from h9 in Enumerable.Range(1, 9)
from i1 in Enumerable.Range(1, 9)
from i2 in Enumerable.Range(1, 9)
from i3 in Enumerable.Range(1, 9)
from i4 in Enumerable.Range(1, 9)
from i5 in Enumerable.Range(1, 9)
from i6 in Enumerable.Range(1, 9)
from i7 in Enumerable.Range(1, 9)
from i8 in Enumerable.Range(1, 9)
from i9 in Enumerable.Range(1, 9)
where (a1 == e5 * e8)
&& (a2 == h1 - 2)
&& (a3 == c5 * e8)
&& (a4 == h9 - 1)
&& (a5 == d7 - e2)
&& (a6 == f1 + g7)
&& (a7 == e3 - h2)
&& (a8 == h6 + a9)
&& (a9 == g3 / g6)
&& (b1 == d1 - a9)
&& (b2 == g2 - h1)
&& (b3 == e5 - 4)
&& (b4 == c7 + 1)
&& (b5 == d7 - 7)
&& (b6 == i5 + d6)
&& (b7 == f8 + 1)
&& (b8 == a1 / i5)
&& (b9 == g3 + 3)
&& (c1 == i2 * a7)
&& (c2 == b4 * a7)
&& (c3 == c6 + 6)
&& (c4 == a2 * f5)
&& (c5 == c6 + 7)
&& (c6 == f8 - i3)
&& (c7 == d6 - 1)
&& (c8 == h8 + 1)
&& (c9 == g4 / c1)
&& (d1 == a7 * 3)
&& (d2 == i3 + a7)
&& (d3 == c2 - e2)
&& (d4 == f4 * i2)
&& (d5 == c4 + 2)
&& (d6 == h9 * e8)
&& (d7 == c4 * a2)
&& (d8 == d1 - a7)
&& (d9 == c1 * d4)
&& (e1 == i1 - e3)
&& (e2 == e3 + 3)
&& (e3 == d1 - g9)
&& (e4 == f1 + d1)
&& (e5 == d1 * 3)
&& (e6 == a5 + 4)
&& (e7 == g6 * h7)
&& (e8 == d9 - 7)
&& (e9 == i3 / e3)
&& (f1 == a3 / i2)
&& (f2 == b7 * e8)
&& (f3 == b6 * d3)
&& (f4 == h2 + 1)
&& (f5 == d1 - 2)
&& (f6 == g5 / b5)
&& (f7 == e3 * h3)
&& (f8 == h2 + h9)
&& (f9 == i1 - 3)
&& (g1 == c5 - f5)
&& (g2 == a6 + 2)
&& (g3 == e6 / a9)
&& (g4 == e8 + 7)
&& (g5 == d6 * a7)
&& (g6 == b1 + 1)
&& (g7 == h1 - 2)
&& (g8 == h5 - f4)
&& (g9 == a8 - a4)
&& (h1 == d2 - i2)
&& (h2 == h4 / i9)
&& (h3 == c7 - 2)
&& (h4 == f9 + 4)
&& (h5 == h2 + 6)
&& (h6 == d8 * 2)
&& (h7 == h1 - e9)
&& (h8 == f5 + 7)
&& (h9 == a1 - b8)
&& (i1 == f3 - b1)
&& (i2 == c9 / h7)
&& (i3 == i1 - c1)
&& (i4 == a6 - 6)
&& (i5 == d5 - d8)
&& (i6 == f6 + 2)
&& (i7 == c7 + 2)
&& (i8 == e3 + i2)
&& (i9 == f6 * g7)
select new
{
a1,a2,a3,a4,a5,a6,a7,a8,a9,
b1,b2,b3,b4,b5,b6,b7,b8,b9,
c1,c2,c3,c4,c5,c6,c7,c8,c9,
d1,d2,d3,d4,d5,d6,d7,d8,d9,
e1,e2,e3,e4,e5,e6,e7,e8,e9,
f1,f2,f3,f4,f5,f6,f7,f8,f9,
g1,g2,g3,g4,g5,g6,g7,g8,g9,
h1,h2,h3,h4,h5,h6,h7,h8,h9,
i1,i2,i3,i4,i5,i6,i7,i8,i9
};
This brute force method will take a heck of a long time to get the final answer.
I ran it for an hour and the results at that point were only:
- a1 to h9 all 1s and
- i1=1, i3=1, i2=1, i4=1, i5=5, i6=1, i7=5, i8=5, i9=7
That is just over 33 000 iterations.
I took this code home and then over 4 hours of re-factoring the "where" clauses into "joins", and then re-ordering the joins, I got to this code:
var solveForNumbers =
from i2 in Enumerable.Range(1, 9)
from i5 in Enumerable.Range(1, 9)
from h2 in Enumerable.Range(1, 9)
from e3 in Enumerable.Range(1, 9)
from a9 in Enumerable.Range(1, 9)
join a7 in Enumerable.Range(1, 9) on e3 - h2 equals a7
join d1 in Enumerable.Range(1, 9) on a7 * 3 equals d1
join b1 in Enumerable.Range(1, 9) on d1 - a9 equals b1
join g6 in Enumerable.Range(1, 9) on b1 + 1 equals g6
join d8 in Enumerable.Range(1, 9) on d1 - a7 equals d8
join h6 in Enumerable.Range(1, 9) on d8 * 2 equals h6
join a8 in Enumerable.Range(1, 9) on h6 + a9 equals a8
join e5 in Enumerable.Range(1, 9) on d1 * 3 equals e5
join b3 in Enumerable.Range(1, 9) on e5 - 4 equals b3
join f5 in Enumerable.Range(1, 9) on d1 - 2 equals f5
join h8 in Enumerable.Range(1, 9) on f5 + 7 equals h8
join c8 in Enumerable.Range(1, 9) on h8 + 1 equals c8
join c1 in Enumerable.Range(1, 9) on i2 * a7 equals c1
join e2 in Enumerable.Range(1, 9) on e3 + 3 equals e2
join i8 in Enumerable.Range(1, 9) on e3 + i2 equals i8
join h5 in Enumerable.Range(1, 9) on h2 + 6 equals h5
join f4 in Enumerable.Range(1, 9) on h2 + 1 equals f4
join d4 in Enumerable.Range(1, 9) on f4 * i2 equals d4
join d9 in Enumerable.Range(1, 9) on c1 * d4 equals d9
join e8 in Enumerable.Range(1, 9) on d9 - 7 equals e8
join a1 in Enumerable.Range(1, 9) on e5 * e8 equals a1
join b8 in Enumerable.Range(1, 9) on a1 / i5 equals b8
join h9 in Enumerable.Range(1, 9) on a1 - b8 equals h9
join a4 in Enumerable.Range(1, 9) on h9 - 1 equals a4
join g9 in Enumerable.Range(1, 9) on a8 - a4 equals g9
join f8 in Enumerable.Range(1, 9) on h2 + h9 equals f8
join b7 in Enumerable.Range(1, 9) on f8 + 1 equals b7
join d6 in Enumerable.Range(1, 9) on h9 * e8 equals d6
join b6 in Enumerable.Range(1, 9) on i5 + d6 equals b6
join c7 in Enumerable.Range(1, 9) on d6 - 1 equals c7
join b4 in Enumerable.Range(1, 9) on c7 + 1 equals b4
join c2 in Enumerable.Range(1, 9) on b4 * a7 equals c2
join d3 in Enumerable.Range(1, 9) on c2 - e2 equals d3
join f3 in Enumerable.Range(1, 9) on b6 * d3 equals f3
join i1 in Enumerable.Range(1, 9) on f3 - b1 equals i1
join e1 in Enumerable.Range(1, 9) on i1 - e3 equals e1
join f9 in Enumerable.Range(1, 9) on i1 - 3 equals f9
join h4 in Enumerable.Range(1, 9) on f9 + 4 equals h4
join i3 in Enumerable.Range(1, 9) on i1 - c1 equals i3
join c6 in Enumerable.Range(1, 9) on f8 - i3 equals c6
join c3 in Enumerable.Range(1, 9) on c6 + 6 equals c3
join c5 in Enumerable.Range(1, 9) on c6 + 7 equals c5
join g1 in Enumerable.Range(1, 9) on c5 - f5 equals g1
join a3 in Enumerable.Range(1, 9) on c5 * e8 equals a3
join f1 in Enumerable.Range(1, 9) on a3 / i2 equals f1
join e4 in Enumerable.Range(1, 9) on f1 + d1 equals e4
join d2 in Enumerable.Range(1, 9) on i3 + a7 equals d2
join h1 in Enumerable.Range(1, 9) on d2 - i2 equals h1
join g7 in Enumerable.Range(1, 9) on h1 - 2 equals g7
join a6 in Enumerable.Range(1, 9) on f1 + g7 equals a6
join a2 in Enumerable.Range(1, 9) on h1 - 2 equals a2
join c4 in Enumerable.Range(1, 9) on a2 * f5 equals c4
join d5 in Enumerable.Range(1, 9) on c4 + 2 equals d5
join d7 in Enumerable.Range(1, 9) on c4 * a2 equals d7
join a5 in Enumerable.Range(1, 9) on d7 - e2 equals a5
join i4 in Enumerable.Range(1, 9) on a6 - 6 equals i4
join g2 in Enumerable.Range(1, 9) on a6 + 2 equals g2
join b2 in Enumerable.Range(1, 9) on g2 - h1 equals b2
join e6 in Enumerable.Range(1, 9) on a5 + 4 equals e6
join g3 in Enumerable.Range(1, 9) on e6 / a9 equals g3
join b9 in Enumerable.Range(1, 9) on g3 + 3 equals b9
join b5 in Enumerable.Range(1, 9) on d7 - 7 equals b5
join e9 in Enumerable.Range(1, 9) on i3 / e3 equals e9
join h7 in Enumerable.Range(1, 9) on h1 - e9 equals h7
join e7 in Enumerable.Range(1, 9) on g6 * h7 equals e7
join i7 in Enumerable.Range(1, 9) on c7 + 2 equals i7
join g5 in Enumerable.Range(1, 9) on d6 * a7 equals g5
join f6 in Enumerable.Range(1, 9) on g5 / b5 equals f6
join i9 in Enumerable.Range(1, 9) on f6 * g7 equals i9
join i6 in Enumerable.Range(1, 9) on f6 + 2 equals i6
join h3 in Enumerable.Range(1, 9) on c7 - 2 equals h3
join f7 in Enumerable.Range(1, 9) on e3 * h3 equals f7
join f2 in Enumerable.Range(1, 9) on b7 * e8 equals f2
join g4 in Enumerable.Range(1, 9) on e8 + 7 equals g4
join c9 in Enumerable.Range(1, 9) on g4 / c1 equals c9
join g8 in Enumerable.Range(1, 9) on h5 - f4 equals g8
where
(e3 == d1 - g9) &&
(a9 == g3 / g6) &&
(h2 == h4 / i9) &&
(i2 == c9 / h7) &&
(i5 == d5 - d8)
select new
{
a1, a2, a3, a4, a5, a6, a7, a8, a9,
b1, b2, b3, b4, b5, b6, b7, b8, b9,
c1, c2, c3, c4, c5, c6, c7, c8, c9,
d1, d2, d3, d4, d5, d6, d7, d8, d9,
e1, e2, e3, e4, e5, e6, e7, e8, e9,
f1, f2, f3, f4, f5, f6, f7, f8, f9,
g1, g2, g3, g4, g5, g6, g7, g8, g9,
h1, h2, h3, h4, h5, h6, h7, h8, h9,
i1, i2, i3, i4, i5, i6, i7, i8, i9
};
I ran the code and then the answer was calculated in a mere 8 seconds.
Conclusion
- LINQ can be used to solve different types of puzzles.
- Using
joins greatly reduces the time spent to find the answer. - Formulas in the sheet which refer back to themselves cannot be added to a
join, and can only be used in the "from" section. This means the LINQ query must *guess* these values. The fewer guesses there are, the faster the answer will be calculated.
Points of Interest
It was fun solving the puzzle using LINQ, but it took about 8 hours of my time. Solving the puzzle using paper only would have been somewhat quicker.
History
- Fixed the type highlighted by SoMad
