Basic Radix-2-FFT algorithm recursive
Derived from the main clause of Fourier:
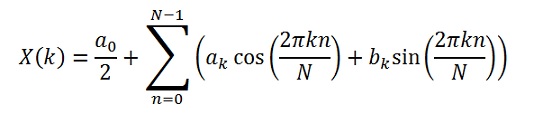
the Radix-2-FFT algorithm for N = 2^j samples is based on the formula:

with M = N/2.
With the substitution u[m] = x[2m] and v[m] = x[2m + 1], we get:

In this formula the two sub-DFT’s

and

are visible and that means the basic Fourier transformation can be split in two sub transformations and these two each can be split in two sub-sub transformations again and so on till we have only two samples left per transformation.
If we start with 8 samples for the first splitting this looks like that

And if we continue to split the flow finally looks like that:

On the first glance it looks quite complicate. The input data is mixed up and there are many arrows in all directions. But if we just look at the first graphic containing one step, we get a simple system. In the formula above we see [2m]-elements are even and [2m+1]-elements are odd elements. That’s why the odd elements are separated from the even ones here. If we look at the first formula and given that the output of one sub transformation overrides the input variables of the transformation, we have to perform the sub transformations and just have to calculate the complex sums after that (given that x[k] is the output of the sub transformation and X[k] the output of this one):








And with




We can replace




And that’s what the first graphic shows.
With a recursive approach this can be put into a quite small algorithm that is a bit easier to be understood than a not recursive one. An important detail to recognize here is possibly that we don’t need the so called bit-reversal here. We just have to separate the odd from the even samples in each recursion as can be seen in the graphic. Quite often that’s not mentioned in descriptions of the Radix-2 algorithm.
Of course the bit-reversal can be done here as well. It would have to be done in the beginning of the algorithm…There are many different ways to implement this transformation.
The recursive procedure would look like that:
public void CalcSubFFT(TKomplex[] a, int n, int lo)
{
int i, m;
TKomplex w;
TKomplex v;
TKomplex h;
if (n > 1)
{
Shuffle(a, n, lo);
m = n / 2;
CalcSubFFT(a, m, lo);
CalcSubFFT(a, m, lo + m);
for (i = lo; i < lo + m; i++)
{
w.real = Math.Cos(2.0 * Math.PI * (double)(i - lo) / (double)(n));
w.imag = Math.Sin(2.0 * Math.PI * (double)(i - lo) / (double)(n));
h = kprod(a[i + m], w);
v = a[i];
a[i] = ksum(a[i], h);
a[i + m] = kdiff(v, h);
}
}
}
With the separation of the odd and even samples:
public void Shuffle(TKomplex[] a, int n, int lo)
{
if (n > 2)
{
int i, m = n / 2;
TKomplex[] b = new TKomplex[m];
for (i = 0; i < m; i++)
b[i] = a[i * 2 + lo + 1];
for (i = 0; i < m; i++)
a[i + lo] = a[i * 2 + lo];
for (i = 0; i < m; i++)
a[i + lo + m] = b[i];
}
}
At the end we have to put that all in one function and divide every element by 2N and element 0 has to be divided by 4N (see main clause of Fourier).
public void CalcFFT()
{
int i;
CalcSubFFT(y, N, 0);
for (i = 0; i < N; i++)
{
y[i].imag = y[i].imag / (double)N * 2.0;
y[i].real = y[i].real / (double)N * 2.0;
}
y[0].imag = y[0].imag / 2.0;
y[0].real = y[0].real / 2.0;
}
Reducing calculation time
As I already found in my article about the quick DFT, we have to calculate many sine and cosine values in these algorithms too. If we want to do a FFT repeatedly in an application, it makes some sense to put all the sine and cosine values into al look up table and just get them from there. That speeds the calculation up quite well.
We create the look up table like
for (i = 0; i < (N / 2); i++)
we[i].real = Math.Cos(2.0 * Math.PI * (double)(i) / (double)(N));
we[i].imag = Math.Sin(2.0 * Math.PI * (double)(i) / (double)(N));
}
And replace the lines
w.real = Math.Cos(2.0 * Math.PI * (double)(i - lo) / (double)(n));
w.imag = Math.Sin(2.0 * Math.PI * (double)(i - lo) / (double)(n));
by
w.real = we[(i - lo)*N/n].real;
w.imag = we[(i - lo)*N/n].imag;
This modification of the algorithm reduced the calculation time for 4096 samples from 5 ms to 3 ms on my computer.
At the DFT algorithm we had to perform a modulo division to get the correct index. Here this is not necessary as we anyway have just sine and cosine values for 0 to 2Pi.
Basic Radix-2-FFT algorithm not recursive
The disadvantage of the easy to be understood recursive approach is that not every environment allows recursive function calls and a bit higher time consumption. All together there are more operations to be done with these shuffles and recursions. Therefore I implemented a not recursive algorithm too. That looks a bit more complicate but it’s worthwhile.
Here we need the Bitreversal function:
public void BitInvert(TKomplex[] a, int n)
{
int i, j, mv = n/2;
int k, rev = 0;
TKomplex b;
for (i = 1; i < n; i++)
{
k = i;
mv = n / 2;
rev = 0;
while (k > 0)
{
if ((k % 2) > 0)
rev = rev + mv;
k = k / 2;
mv = mv / 2;
}
{
if (i < rev)
{
b = a[rev];
a[rev] = a[i];
a[i] = b;
}
}
}
}
For each index “I” runs through all the bits by “k” and inverts them. The modulo division tells me whether the least significant bit is 1 or 0 and has to be put in reversed index or not. Starting at the most significant bit. Dividing k by 2 moves the second least significant bit one position to the right. In this way we get all the bits from least significant trough most significant and have the reversal in “rev”. Now we just have to switch the index “i” and “rev”. But just replace if “I” is smaller the “rev”. Otherwise we change all the indexes back if “I” becomes bigger than “rev”.
After this bit reversal we can calculate the sub FFT by:
public void CalcSubFFT(TKomplex[] a, int n)
{
int i, k, m;
TKomplex w;
TKomplex v;
TKomplex h;
k = 1;
while (k <= n/2)
{
m = 0;
while (m <= (n-2*k))
{
for (i = m; i < m + k; i++)
{
w.real = Math.Cos( Math.PI * (double)(i-m)/(double)(k));
w.imag = Math.Sin( Math.PI * (double)(i-m)/(double)(k));
h = kprod(a[i + k], w);
v = a[i];
a[i] = ksum(a[i], h);
a[i + k] = kdiff(v, h);
}
m = m + 2 * k;
}
k = k * 2;
}
}
These two functions have to be put in main call and all the elements have to be divided by 2N and element 0 has to be divided by 4N.
public void CalcFFT()
{
int i;
BitInvert(y, N);
CalcSubFFT(y, N);
for (i = 0; i < N; i++)
{
y[i].imag = y[i].imag / (double)N * 2.0;
y[i].real = y[i].real / (double)N * 2.0;
}
y[0].imag = y[0].imag / 2.0;
y[0].real = y[0].real / 2.0;
}
Reducing calculation time
And if we finally put the sine and cosine values into a look up table:
we = new TKomplex[N / 2];
for (i = 0; i < (N / 2); i++)
{
we[i].real = Math.Cos(2* Math.PI * (double)(i) / (double)(N));
we[i].imag = Math.Sin(2* Math.PI * (double)(i) / (double)(N));
}
And replace
w.real = Math.Cos( Math.PI * (double)(i-m)/(double)(k));
w.imag = Math.Sin( Math.PI * (double)(i-m)/(double)(k));
by
w.real = we[((i-m)*N / k/ 2)].real;
w.imag = we[((i-m)*N / k / 2)].imag;
That reduces the calculation time for the transformation by approx. 30 % as well. There is no difference in time consumption visible compared to the recursive algorithm as long as we just run the transformation once. But if we run it 10 times the difference becomes visible:
Comparison of time consumption while 10 transformations whit 4096 samples:
| | Calculation time
|
| Recursive standard
| 45 ms
|
| Recursive with look up table
| 30 ms
|
| Not recursive standard
| 41 ms
|
| Not recursive with look up table
| 24 ms
|
For more math visit www.mosismath.com :-)
