Introduction
In this article I want to show you how we can query a family tree using LINQ. This article is
a deep dive into the LINQ technology and how it becomes very powerful in combination with Dynamic Programming.
This time I'll use Prolog style to achieve my goal, to make it easier and more understandable.
Background
A family tree is chart representation of family relationships in a tree structure.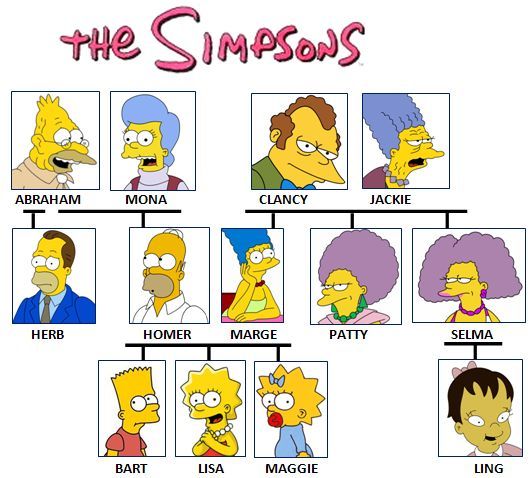
Family trees are often presented with the oldest generations at the top and the newer generations at the bottom.
The figure represents a sample of family trees (The Simpsons). I know it's funny 
, but it
will make our idea simple and clear. Of course the rest of the article will be interesting
because many of us know the Simpsons. The figure illustrates how the family tree will look like, how we can organize the family members, and so forth.
The figure consists of
three generations, the first generation at the top of the tree and the third generation at the bottom.
Such
a tree describes the relationships of each node, e.g., Bart is son of Homer who is spouse of Marge. So we can know every
relationship in the family including fathers, mothers, brothers, sisters, sons, daughters, grand parents .. etc.
This is a true sample for
a tree structure which is already taught in Data Structures books.
In the following sentences I want
to introduce Prolog briefly, which is a general purpose logical programming language that's used widely in artificial intelligence (AI). Prolog is one of the
many functional programming languages. What does that mean? It means everything in this language is functional!!
May be that sounds strange , don't worry
I'll try to explore an example with a little details.
Prolog programs describe relations, defined by means of clauses. Clauses can be facts or rules.
male(homer).
father(homer, bart).
The facts in Prolog are nothing but functions with some arguments ending with
a comma. If we take a look at the above box we'll notice that Male, Female, and Father are facts. To make it clear we can say Homer is a Male and Homer is Father of Bart.
In a nutshell it seems to be an "Is A" relationship.
brother(X,Y):- male(X), father(Z,X), father(Z,Y).
A rule in Prolog is a kind of function that has a body which defines the actual function. In the above box we have a Brother rule which says X is Brother of Y will be true if X is Male and if we find Z as Father of X as
well as Father of Y.
I think it's easy. Now you can start to define your own facts and rules in Prolog, which
are the essential things in that language. The remaining thing is evaluation which is a kind of query engine for Prolog,
because all the facts and rules have been stored in the knowledge database. The user can ask the Prolog query engine as much as he/she wants. Then engine starts to evaluate and answer these questions. Here
are a couple of queries.
?- male(homer).
Yes
?- father(bart, homer).
No
?- father(X, bart).
X=homer
The first query asks if Homer is a Male. Prolog will check this fact and return the result which in this case
is Yes; same thing in the second one. If we take a deep look at the last query we'll notice that we have X which
is a variable, all the names starting with a capital letter are considered as variables, so this time Prolog
will search for someone who is a Father of Bart, and Prolog will respond with X=Homer.
I think this
is a quick tour of Prolog .. let us enter the mission ..
Using the code
We have seen Prolog and how it uses the knowledge database and query engine for reasoning.
'GEN 1: Abraham Mona Clancy Jackie
' | | | |
' +---o-----o---+ +---o-----o-----o---+
' | | | | |
'GEN 2: Herb Homer Marge Patty Selma
' | | |
' +---o-----o-----o---+ o
' | | | |
'GEN 3: Bart Lisa Maggie Ling
The above diagram explores the Simpsons family tree. It shows every member of the family in each generation.
It is good to draw it right here because the rest of the demos will use the tree, and it
will be easier to discover the relationships and follow the rules that we will construct later on.
Now I
want to build my LINQ to Family Tree provider with Prolog flavor. And the interesting part for me is the query engine which
I'm trying to explore in this article because it's the core part for reasoning and evaluating results.
Again as per my latest tip/trick
in which I introduced LINQ to CSV I realize that
a combination of LINQ and Dynamic Programming makes LINQ so sweet and more powerful to LINQfy dynamic objects.
The same way I was thinking of constructing a LINQ to Family Tree.
Fact class
Class Fact
Inherits DynamicObject
Public Property Name As String
Public Property Arguments As New List(Of String)
Public Overrides Function TryInvokeMember(binder As InvokeMemberBinder, _
args() As Object, ByRef result As Object) As Boolean
Select Case args.Length
Case 1
mFacts.Add(New Fact() With {.Name = binder.Name.ToProper(), _
.Arguments = New List(Of String) From {args(0)}})
Case 2
mFacts.Add(New Fact() With {.Name = binder.Name.ToProper(), _
.Arguments = New List(Of String) From {args(0), args(1)}})
End Select
Return True
End Function
End Class
The Fact class is one of the essential classes that participate
in the core class FamilyTree. It defines a simple fact which contains two properties Name which holds the name of the fact such as Male, Female, Father, Brother .. etc.,
Arguments which is a list of strings that holds all the arguments that are related to the fact.
E.g., Female(Amy), Parent(Neal,Ian). The arguments contain "Amy" as parameter for the
Female fact, and two parameters "Neal" and "Ian" for the
Parent fact.
We will notice that the Fact class inherits from
DynamicObject which makes this class capable to contain run-time functions which
are pretty neat, because it allows us to add facts as much as we want at run-time without complaining.
The
Fact class must be dynamic because if we take a look at a Prolog sample we will notice that we can write any name and
make it a fact, which is something strange in the non dynamic world!! The question is how to make this class flexible and contain run-time functions?!!
DynamicObject comes to the rescue.
<Extension()>
Public Function ToProper(str As String) As String
Return StrConv(str, VbStrConv.ProperCase)
End Function
ToProper is an extension method which convert any string to a proper case which is something useful, perhaps the user writes a fact
Female("Amy") and a query for Female("amy"), the result will absolutely be false because the name is case sensitive in comparing strings.
To avoid this I introduced this helper function.
The last thing in the Fact class is the fact creation which is simply done by overriding
the TryInvokeMember method, which gives us an opportunity to write some code while invoking any function inside this class. The code is straightforward which pushes a new instance of
the Fact class into the mFacts property which is declared in
the FamilyTree class. It simply holds all the facts in the family tree.
I just want to point out that binder.Name returns the actual name after ".".
For example fact.Father = ...
Rule class
Class Rule
Inherits DynamicObject
Public Property Name As String
Public Property Definition As Func(Of String, String, Boolean)
Public Overrides Function TrySetMember(binder As SetMemberBinder, value As Object) As Boolean
mRules.Add(New Rule() With {.Name = binder.Name, .Definition = value})
Return True
End Function
End Class
The Rule class defines a simple rule which takes the same way of Fact into participation
in the FamilyTree class. It has two properties: Name which holds the rule name and
Definition which holds the actual body of the function. As we can see it's a Func delegate which points to a function that accepts two strings and returns a boolean, because all the rules accept two arguments as input and it has some logic to check whether the rule
is satisfied or not.
This time we override TrySetMember. Actually we want
to create a run-time property that holds a function, so it's setting a member rather than invoking
a member. The same thing happens when the code pushes a new instance of the
Rule class into the mRules property which is defined in the
FamilyTree class to hold all the rules in the tree.
I want
to point out that the value is the actual value set by programming which supposedly comes after the "=", for example, r.Brother = ... which is the function that defines the
Brother rule in this case.
FamilyTree class
The
FamilyTree class is the core class in LINQ to FamilyTree which acts as query engine for Prolog, It's
a little long so I will try to divide it into chunks to make it readable and more understandable.
Public Class FamilyTree
Inherits DynamicObject
Private Shared Property mFacts As New List(Of Fact)
Private Shared Property mRules As New List(Of Rule)
Again and again this class is a dynamic object to allow us to create run-time functions for querying as much as we need. Basically it contains two important properties
mFacts, mRules which we had already seen before in the previous classes, so they 're
Private Shared to make them accessible with the FamilyTree class and all inner classes inside it - which in our case
are Fact and Rule:
Public Sub New()
mRules.Add(New Rule() With {.Name = "Parent", _
.Definition = New Func(Of String, String, Boolean)(Function(x, y)
Return mFacts.Where(Function(f) f.Name = "Parent" AndAlso _
f.Arguments.First() = x AndAlso f.Arguments.Last() = y).Any()
End Function)})
mRules.Add(New Rule() With {.Name = "Married", _
.Definition = New Func(Of String, String, Boolean)(Function(x, y)
Return mFacts.Where(Function(f) f.Name = "Married" AndAlso _
f.Arguments.First() = x AndAlso f.Arguments.Last() = y).Any()
End Function)})
mRules.Add(New Rule() With {.Name = "Male", _
.Definition = New Func(Of String, String, Boolean)(Function(x, y)
Return mFacts.Where(Function(f) f.Name = "Male" AndAlso f.Arguments.First() = x).Any()
End Function)})
mRules.Add(New Rule() With {.Name = "Female", _
.Definition = New Func(Of String, String, Boolean)(Function(x, y)
Return mFacts.Where(Function(f) f.Name = "Female" AndAlso f.Arguments.First() = x).Any()
End Function)})
End SubWe add the four essential rules that we need in the constructor:
Parent, Married, Male, and Female. Let me describe two of them.
Parent: which has name "Parent" and the definition is
a simple function that accepts x, y as arguments and checks if there's a fact that has name "Parent" and x as first argument and y as last argument; if
there is it will return True otherwise False. Male: which has name "Male" and the definition is a simple function that accepts x, y as arguments and check if there's a fact that has name "Male" and x as first argument; if
there is, it will return True otherwise False. If you notice we are no longer interested in the last argument
because this fact has a single argument.
Public Sub Facts(action As Action(Of Object))
action(New Fact())
End Sub
Public Sub Rules(action As Action(Of Object))
action(New Rule())
End SubAs we have seen I introduced new procedures to add facts and rules, respectively, but I used
Action(Of T) instead of pushing the instances directly into the facts or rules lists!
Don't worry I did that to add the facts or rules at one shoot, in other words as
a bulk of instances rather than adding them one by one. Also to make it look like a function that we have seen in Prolog before.
Public Overrides Function TryInvokeMember(binder As InvokeMemberBinder, _
args() As Object, ByRef result As Object) As Boolean
Dim mRule = mRules.Where(Function(r) r.Name = binder.Name).SingleOrDefault()
If mRule IsNot Nothing Then
Dim lst As New List(Of String)
Dim lst1 As List(Of String)
Dim lst2 As List(Of String)
If args(0).GetType() Is GetType(String) Then
lst1 = New List(Of String)
lst1.Add(args(0).ToString().ToProper())
Else
lst1 = New List(Of String)(CType(args(0), List(Of String)).Select(Function(s) s.ToProper()))
End If
Select Case args.Length
Case 1
If binder.Name = "Male" OrElse binder.Name = "Female" Then
result = mRules.Where(Function(r) _
r.Name = binder.Name).Single().Definition.Invoke(args(0), Nothing)
Exit Select
End If
For Each item1 In lst1
lst.AddRange(mFacts.Select(Function(f) f.Arguments.First()).Distinct().Where(_
Function(f) f <> item1 AndAlso mRule.Definition.Invoke(f, item1)))
Next
result = lst
Case 2
If args(1).GetType() Is GetType(String) Then
lst2 = New List(Of String)
lst2.Add(args(1).ToString().ToProper())
Else
lst2 = New List(Of String)(CType(args(1), _
List(Of String)).Select(Function(s) s.ToProper()))
End If
For Each item1 In lst1
For Each item2 In lst2
If mRule.Definition.Invoke(item1, item2) Then
result = True
Exit Select
End If
Next
Next
result = False
End Select
Else
Throw New ArgumentException(String.Format("The rule {0} is not exist", binder.Name))
End If
Return True
End Function
Here I override the TryInvokeMember method to execute the queries that are associated
with the FamilyTree object. I know it looks strange a little bit, but hold on I will give you the main idea and
explain how it works.
Basically we are looking for a rule with its name after the ".". If we issue
familyTree.Brother that means we should look for
the Brother rule in mRules list; if it does not exist that means it's not defined yet so I throw
an ArgumentException,
otherwise we have two choices:
- Boolean Query: If the query contains two arguments that indicate that we want to check if the given rule satisfies or not.
May be the query contains one argument and this is a special case for Male
and Female rules.
- List Query: If the query contains one argument that indicates the we
are looking for something that satisfies the argument with the given rule.
If we dig into the previous code we will see that I introduced two List(Of String) because sometimes one or both arguments may contain more than one value. For example
the Sister rule which is defines as follows:
sister(X,Y):- female(X), sibling(X,Y)
X may have one or more siblings, I think it will be nice if we use
List(Of String) rather than String to cover all the cases.
Again if we dig into the code you will notice that whenever we
are trying to execute a List Query we are looking into all the facts of the tree which in
the mFacts property. Aafter that we return all the matches that satisfy the given rule.
That's it .. let us see how we can represent Simpsons in
a FamilyTree object, of course we should create an instance of
FamilyTree class as follow:
Dim family As Object = New FamilyTree()
After that let us define our facts which are shown in the graph at the top.
family.Facts(New Action(Of Object)(Sub(f)
f.Male("Abraham")
f.Male("Clancy")
f.Male("Herb")
f.Male("Homer")
f.Male("Bart")
f.Female("Mona")
f.Female("Jackie")
f.Female("Marge")
f.Female("Patty")
f.Female("Selma")
f.Female("Lisa")
f.Female("Maggie")
f.Female("Ling")
f.Married("Abraham", "Mona")
f.Married("Clancy", "Jackie")
f.Married("Homer", "Marge")
f.Parent("Abraham", "Herb")
f.Parent("Mona", "Herb")
f.Parent("Abraham", "Homer")
f.Parent("Mona", "Homer")
f.Parent("Clancy", "Marge")
f.Parent("Jackie", "Marge")
f.Parent("Clancy", "Patty")
f.Parent("Jackie", "Patty")
f.Parent("Clancy", "Selma")
f.Parent("Jackie", "Selma")
f.Parent("Homer", "Bart")
f.Parent("Marge", "Bart")
f.Parent("Homer", "Lisa")
f.Parent("Marge", "Lisa")
f.Parent("Homer", "Maggie")
f.Parent("Marge", "Maggie")
f.Parent("Selma", "Ling")
End Sub))
The code is straightforward, we create a new Action(Of Object)
and we pass all the facts that we have. It is like a Prolog fact except it passes arguments as a magic string, but it's more readable. And as
I mentioned before we have four essentials rules (Male, Female,
Married, and Parent) which are predefined in my LINQ to Family Tree provider. Isn't that cool? I hope that .. there are a lot of cooler things
to continue ..
After we define our facts it's time for defining the rules or family relationships ..
family.Rules(New Action(Of Object)(Sub(r)
r.Spouse = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Married(x, y) OrElse family.Married(y, x)
End Function)
r.Husbund = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso family.Spouse(x, y)
End Function)
r.Wife = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Female(x) AndAlso family.Spouse(x, y)
End Function)
r.Father = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso family.Parent(x, y)
End Function)
r.Mother = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Female(x) AndAlso family.Parent(x, y)
End Function)
r.Sibling = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return Equals(family.Father(x), family.Father(y)) AndAlso _
Equals(family.Mother(x), family.Mother(y)) AndAlso x <> y
End Function)
r.Brother = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso family.Sibling(x, y)
End Function)
r.Sister = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Female(x) AndAlso family.Sibling(x, y)
End Function)
r.GrandParent = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Parent(x, family.Parent(y))
End Function)
r.GrandFather = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso family.GrandParent(x, y)
End Function)
r.GrandMother = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Female(x) AndAlso family.GrandParent(x, y)
End Function)
r.GrandChild = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.GrandParent(y, x)
End Function)
r.GrandSon = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso family.GrandChild(x, y)
End Function)
r.GrandDaughter = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Female(x) AndAlso family.GrandChild(x, y)
End Function)
r.Child = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Parent(y, x)
End Function)
r.Son = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso family.Child(x, y)
End Function)
r.Daughter = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Female(x) AndAlso family.Child(x, y)
End Function)
r.Uncle = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso (family.Sibling(x, family.Parent(y)) _
OrElse family.Parent(family.Sibling(family.Spouse(x)), y))
End Function)
r.Aunt = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Female(x) AndAlso (family.Sibling(x, family.Parent(y)) _
OrElse family.Parent(family.Sibling(family.Spouse(x)), y))
End Function)
r.Cousin = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Uncle(family.Parent(x), y) OrElse family.Aunt(family.Parent(x), y)
End Function)
r.Nephew = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso family.Sibling(family.Parent(x), y)
End Function)
r.Niece = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Female(x) AndAlso family.Sibling(family.Parent(x), y)
End Function)
r.GreatGrandParent = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Parent(x, family.GrandParent(y))
End Function)
r.GreatGrandFather = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso family.GreatGrandParent(x, y)
End Function)
r.GreatGrandMother = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Female(x) AndAlso family.GreatGrandParent(x, y)
End Function)
r.GreatGrandChild = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Parent(family.GrandChild(y), x)
End Function)
r.GreatGrandSon = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso family.GreatGrandChild(x, y)
End Function)
r.GreatGrandDaughter = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Female(x) AndAlso family.GreatGrandChild(x, y)
End Function)
r.ParentInLaw = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Parent(x, family.Spouse(y))
End Function)
r.FatherInLaw = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso family.ParentInLaw(x, y)
End Function)
r.MotherInLaw = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Female(x) AndAlso family.ParentInLaw(x, y)
End Function)
r.SiblingInLaw = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Sibling(x, family.Spouse(y))
End Function)
r.BrotherInLaw = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso family.SiblingInLaw(x, y)
End Function)
r.SisterInLaw = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Female(x) AndAlso family.SiblingInLaw(x, y)
End Function)
r.ChildInLaw = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Spouse(x, family.Child(y))
End Function)
r.SonInLaw = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso family.ChildInLaw(x, y)
End Function)
r.DaughterInLaw = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Female(x) AndAlso family.ChildInLaw(x, y)
End Function)
End Sub))
As I did in facts, I defined almost the rules passed in a new instance of
Action(Of Object) that will be passed into the Rules procedure.
Let me now explain three of them:
1. Father
r.Father = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso family.Parent(x, y)
End Function)
I define a dynamic member named Father that holds a function which accepts two strings and returns a boolean.
In other words it holds a rule definition. The function is very simple Father(x, y). x is Father of y if x is male and x is Parent of y.
If these two conditions are satisfied then x should be a father of y.
2. Sibling
r.Sibling = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return Equals(family.Father(x), family.Father(y)) AndAlso _
Equals(family.Mother(x), family.Mother(y)) AndAlso x <> y
End Function) I define a dynamic member named Sibling that holds a rule. Sibling(x, y). x
is Sibling of y if father of x is the same exact Father of y as well as their Mother and x is not y. Here I used a helper function
Equals because we are issuing a list query and we know that = operator is not
appropriate for comparing two lists, so I used the following:
Public Function Equals(lst1 As List(Of String), lst2 As List(Of String)) As Boolean
Return lst1.Intersect(lst2).Any()
End Function
3. Uncle
r.Uncle = New Func(Of String, String, Boolean)(Function(x, y) As Boolean
Return family.Male(x) AndAlso (family.Sibling(x, family.Parent(y)) _
OrElse family.Parent(family.Sibling(family.Spouse(x)), y))
End Function)
I define a dynamic member named Uncle that holds a rule. Uncle(x, y). x is
Uncle of y if x is male and Parent of y is sibling to x. We pass a function as argument to another function and that's the flavor of functional programming languages
such as Prolog.
Knowledge Database
The knowledge database is a data structure that consists of two parts:
1. Facts
A linear data structure that all the facts in the family tree are organized into.
It simply contains all the fact names and their arguments they are associated with.
2. Rules
A linear data structure that all the rules in the family tree are organized into.
It simply contains all the rule names and definitions.
How the query engine works?
The query engine is the part that is responsible for executing queries and evaluating the result from the knowledge database.
1. Boolean Query
In this type of query,
the engine works as the follows:
- Initialize the query
- Look into
the Facts data structure - which is
mFacts in our code - to the exact same fact name that has been issued with their arguments - Return true if we find a match in facts
- Otherwise
look into the Rules data structure to the exact rule name that has been issued with the
arguments
- If the rule definition contains a declaration of predefined
facts, just apply the rule definition with the given arguments and return
the list of names that satisfy the rule definition in Facts
- If the rule definition contains another rule, we should dig into that rule and do the same thing
as in the previous step
2. List Query
In this type of query, the engine works as follows:
- Initialize the query
- Look into
the Rules data structure - which is
mRules in our code - to the exact rule name that has been issued with its argument - Return the definition of the rule if found
- Apply that rule with the given argument with all the names in facts
- Return the list of names that match the previous rule
Last but not least let us issue some queries and see their results:
Console.WriteLine(family.Mother("Selma", "Ling"))
True
Console.WriteLine(family.Sister("Ling", "Lisa"))
False
Dim query = From s In CTypeDynamic(Of List(Of String))(family.Daughter("Homer"))
Select s
For Each item In query
Console.WriteLine(item)
Next For Each item In query
Lisa
Maggie
The first query returns True because Selma is Female and she is a Parent of Ling, so Selma is Mother of Ling. While the second query returns
False because Ling is not a Sibling of Lisa.
The above queries
are a sample of Boolean Query, while the last query is a sample of a List query,
it uses LINQ to enumerate all of Homer's daughters, which are in our case Lisa and Maggie.
The last thing I want to show you is one of the complex queries using LINQ to Family Tree:
Dim query = From gc In CTypeDynamic(Of List(Of String))(family.GrandFather("Bart"))
Let Children = family.Child(gc)
Where Children.Count > 1
Select Name = gc, Children
For Each item In query
Console.WriteLine("{0} ({1}) childern", item.Name, item.Children.Count)
For Each subitem In item.Children
Console.WriteLine(" {0}", subitem)
Next
Console.WriteLine()
Next
Abraham (2) children
Herb
Homer
Clancy (3) children
Marge
Patty
SelmaIn the above query, we were looking for the GrandFathers of Bart, Abraham
and Clancy, and retrieving their names and their children if they have more than
one child. Of course the result will show Abraham, Clancy, and their children.
That's it .. I hope you enjoyed my LINQ to Family Tree provider.
Points of Interest
LINQ is a great technology for querying with any underlying data source, and
to mix with Dynamic Programming to explore its power. In this article I solved some of
the tiny issues such as capitalization of arguments, optimizing the search process, and detecting undefined rules.
