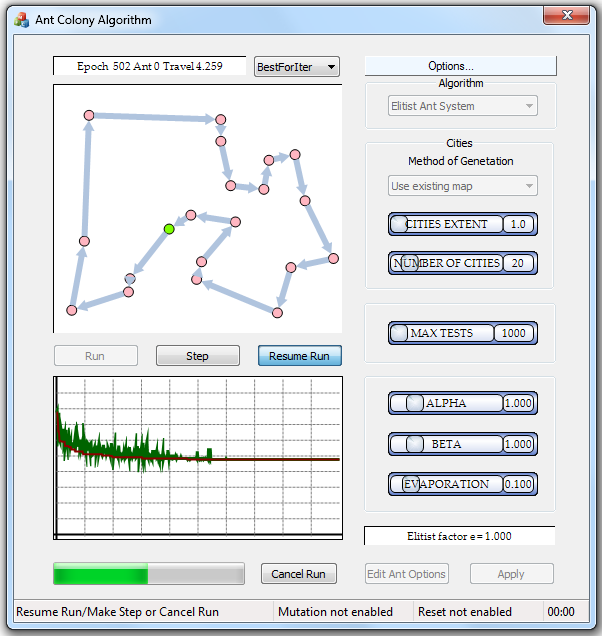
Application main dialog
Table of Contents
Introduction
I was always interested in Artificial Intelligence problems.
So when I saw the article "Genetic
and Ant Colony Optimization Algorithms" by Peter Kohout, I immediately
downloaded it. The article was about solutions of a Traveling Salesman
Problem. While I was reading the article and its code, it occured to me that a math
graph might be a natural mathematical model for this problem. Out of pure
curiosity, I decided to rewrite the code using the Boost Graph Library. In the
process of writing code, I learned about other Artificial Ant
algorithms. I decided to add them to the code. I wanted to look deeper into the
algorithm's behavior, so I added several statistics to calculate. I added means
to present these statistics as graphic charts. I also added means to view and peruse
as many graph snapshots at runtime as the user needed. I added
serialization of configurations and trip results into XML files, and
possibilities to load and run external ant colony configurations and graph
snapshots of them. I added the routines to print graph snapshots as tables, and
reports for the best to-date solutions. In the end, I had an application with
a very different user interface and a very different code.
The application has an open-end architecture. You can very
easily add new algorithms and statistics to the application not changing most of the
application code.
The AI aficionados will find there possibilities to play with
algorithms of Artificial Ant Colony Optimization and their parameters. They
will be able to look at every step of the proceedings.
The algorithms implemented are:
- Ant System
- Elitist Ant System
- Ranked Ant System
- Best-Worst Ant System
- Min-Max Ant System
- Ant Colony
These algorithms are discussed below.
I hope that people not interested in AI at all will still
find something for themselves in the app code. It might be:
- Use of the object factory design patterns
- Use of
TypeList templates for registration of objects with
factories - C++ lambda expressions in STL algorithms
- Thread synchronization with events
- Customization of the MFC
CPrintDialog class - Implementation of a rather complicated user interface
and other things.
Anyway, I wish you good reading.
Acknowledgements
Definitions
of Ant Colony Optimization algorithms can be found in the book Ant
Colony Optimization by Marco Dorigo and Thomas Stützle. Most of the content
of this book is accessible via Google Preview on the book's web page. Also very
useful was Ant
Colony Optimization for Tree and Hypertree Decompositions, Master Thesis by
Thomas Hammerl of Vienna.
I also used ACOTSP
Software by Thomas Stützle. This software
is written in C under Unix OS. I used it as a reference to Ant Colony
Optimization algorithms.
I want to thank Igor Tandetnik for his very useful
recommendations in reply to my inquires on MSDN Developers Forums.
Preliminaries
To compile and link the code I
used MS Visual Studio 2012 Ultimate Update 3. Because I used my ChartCtrlLib
library in the code the project requests an addition of the preprocessor
directive _VARIADIC_MAX=10 to the project properties. The debug and release
versions of the library are in the Debug and Release folders of the
solution directory.
All code can be compiled
under MS Visual Studio 2010, but you will have to start a new solution
and manually import the project properties from the VS 2012 solution. The source
code should not be changed.
In this application, I used the
static MFC library ChartCtrlLib.lib, and the proprietary slider control
CSliderGdiCtrlT. You can get detailed information on the library from my
article An
MFC Chart Control with Enhanced User Interface,
and about the slider from SliderGdiCtrl:
Yet Another Slider Control - Accepts (Almost) All POD Types and Uses
GDI+. Headers for both controls and the compiled library are included in
the zip files for this project. The part of information about the use of TypeLists
is in my article Object
Factory Design Pattern: Register Creator Functions Using TypeLists and Template
Metaprogramming. Code for the static library and for the slider seamlessly compile under Visual Studio 2012.
You will need the Boost Graph
Library. I used Boost v. 1_51.0. You can download it from Boost site or use BoostPro
1.51.0.0 Installer.
All
custom controls are built with GDI+.
You will
need all this information if you are adding your own algorithms to this
application.
The Traveling Salesman Problem
The quote from the "Ant Colony Optimization": The
Traveling Salesman Problem is a problem of a salesman who, starting from his
hometown, wants to find the shortest tour that takes him through a given set of
customer cities and then back home, visiting each customer city exactly
once." Each city is accessible from all other cities.
Ant Colony Optimization Algorithms
In all Ant Colony Optimization algorithms, each ant gets
a start city. Beginning from this city, the ant chooses the next city according
to algorithm rules. After visiting all customer cities exactly once, the ant
returns to the start city. The ants might travel concurrently or in sequence.
Each ant deposits some amount of pheromone on his path. The amount of pheromone
depends on the quality of the ant's path: a shorter path usually results in a
greater amount of pheromone. The deposited pheromone suffer from evaporation.
The algorithms use different rules for selection of
the next city to move to, for evaporation, and for deposition of pheromone.
A nightmare of each optimization algorithm is to be stuck forever
in some locally optimal loop.
Different techniques to escape such loops were developed for
different Ant Colony Optimization algorithms.
This application implements six known algorithms so far:
- Ant System
- Elitist Ant System
- Ranked Ant System
- Best-Worst Ant System
- Min-Max Ant System
- Ant Colony
Each algorithm might be run with mutation and/or restart
options enabled or disabled.
I did not invent any of these algorithms. I used sources I
listed in the Acknowledgments section of this article with minor
modifications. Symbols in the algorithm equations below are the same as they are in
the sources listed in Acknowledgments.
Ant System
The Ant System Optimization algorithm is the first algorithm
proposed and analyzed by Marco Dorigo.
Construct solutions
Initially every path between cities
has some initial amount of pheromone. Each ant starts from a randomly
assigned city and goes from a city to the next city until all cities are
visited exactly once. From the last visited city the ant returns to the start
city.
The ant in city i selects
the next city to visit by calculating probabilities:
Here
- sp - partial solution #p
- N - set of all paths from the city i to all
adjacent cities still not visited by the ant
- cij - path from the city i to the city j
- p - probability
- tij -
amount of pheromone on the path cij
- hij -
some heuristic factor, usually
,
where dij is a distance between cities i
and j, Q is some constant
- α and β - algorithm parameters.
The ant compares for
each j to be traveled to some random number.
If ,
the ant immediately moves to the city j. It means that the ant does not
always select the path with maximal pheromone, thus diminishing chances to get
caught into a local loop.
There always is a very, very tiny
probability of never satisfying the condition.
So in this application I use a modification proposed in Ant
Colony Optimization. For the given city i I still generate a random
number but
compare it to the moving sum.
The sum is updated with each new calculated.
The first j that gives is
the index of the next city to move. Actually, this modification makes
a difference only in the very first trial's steps, when the pheromones deposited
on the travel paths are very close to each other. At the end of the test, the
ant usually takes the maximum p path.
The ants travel concurrently. It
means that there is no pheromone correction until all ants return to their
start cities.
Pheromone Update
The ants update pheromones on paths
connecting the cities according to the formula:
where
- m - number of ants,
- if
the ant k traveled the path between cities i and j; Q is some constant, and Lk is the length of the kth
ant's travel
- 0
otherwise.
In this application, Q is a
city's extent, i.e. the side of the least square that contains all cities.
Because Q appears only as a numerator in fractions where
denominators are distances, it keeps the results independent of the scale of
the city's coordinates.
There are very different recommendations
related to the values of α, β, <stromg>ρ,
start values of pheromone, and the number of ants (ρ is an evaporation factor, see below). One article recommends α = 1, β=2,
ρ=0.5, and start pheromone
t=1/m, where m is
the number of cities. Anyway, you can play with them in this application.
It seems that the number of ants is not
so important if there is enough number of trials, so set of the start cities for each ant could
contain all customers' cities. In this application, we employ only ten ants.
Evaporation
After all ants complete their nth
trip, evaporation is applied to all paths between cities:
(3)
Here is
the evaporation factor.
There is a question of when to apply
global evaporation: immediately after all ants complete their trip, or after
all pheromones on graph edges (paths between cities) are updated? Evaporation
before updates is, essentially, increase of updating pheromones.
In literature, some authors apply a (1 - ρ) multiplier to all
pheromones, some others do not.
I found that evaporation after
updates sometimes prevents the appearance of local non-optimal loops, so in this
application global evaporation is applied to graph edges last, after
pheromone updates.
Elitist Ant Algorithm
The solution construction and evaporation are as defined by
equations (1) and (2) in the Ant System Algorithm.
The pheromone update is a little bit different: on each iteration,
the best to date ant deposits an additional quantity of pheromone on paths it
traveled:
Here if
the path ij is from Tbs,
Tbs is the best to date round trip, e is an algorithm's
parameter. It was reported, that the best value for e is between four
and six.
Note that this algorithm keeps depositing an additional
pheromone on the same paths until the best to date solution is changed.
Probably, you might want to try mutations and/or resets with that algorithm.
Rank-Based Ant System
Again, the difference is in the pheromone update.
For each of iterations, the best to date ant and additionally
the w-1 best ants for this iteration are selected. The best to date and
each of the selected ranked ants deposit pheromone on paths they travel:
Q is a constant, Lr is the length of the rth
ant trip, e is the additional multiplier. Again, the best results are at
The member is
similar to the Elitist Ant Algorithm parameter for the best to date ant.
Best-Worst Ant Algorithm
I used
Analysis
of Best-Worst Ant System.. by Oscar Cordon and others. The solution construction is defined by (1), and evaporation
rule is as in (3).
Only the best to date ant updates pheromones:
Here if
the path ,
Tbs is the best to date round trip, Cbs -
length of the trip.
In addition, the paths of the round trip of the worst ant
for the current iteration that are not in the best to date solution are subject
to additional evaporation:
Here ρw
is an additional evaporation factor for all and ,
Tw is the worst solution for the given iteration, and Tbs
is the best to date solution.
Usually this algorithm includes a mutation of the
pheromone on selected paths of the trail, and the algorithm we resets all pheromones to the initial value and restart search for the best solution when the process seems stuck.
In this application, mutation and restart are options. You
can add them to any algorithm.
Min-Max Ant System
The solution construction is according to the equation (1).
There are variants in the selection of the ants allowed to
update pheromones: the best to date ant, or the best for current iteration, or the
best after latest reset ant, or the best to date ant for even iterations, and the
best for iteration for odd iterations.
There are min and max pheromone limits to the quantity of
pheromone on the paths between cities, τmin
and τmax. It
is believed that prevents local loops. So, evaporation is:
The update is:
Here if
the path Tsel
is a selected ant's round trip, Csel - is the length of the trip.
Some authors initiate pheromones to τmax, but in this application
I am using τ0 = 1/ncities.
Ant Colony System
In all previous algorithms pheromones were updated only
after all ants completed travel for a given iteration. Ant Colony System
is different. After an ant moves from one city to the next, the
pheromone on the traveled path is reduced by some value. The solution
construction is also different.
Solution Construction
The algorithm has a parameter.
The parameter sets the boundary between two rules to select the next city. On
each step, the algorithm generates a random number.
If,
the next city to move is selected according to (1); else index j
of the next city to move is:
where
- i is the index of the current city,
- j is the index of the city to move next,
- is
a set of cities adjacent to the current city i at step k,
- τil is
the amount of pheromone on the path cil,
- ,
Q is a constant (in this app it is a city's extent), dil
is a distance between the cities i and l,
- β - algorithm
parameter
After the ant moves from the city i
to city j, the pheromone on the path cij is evaporated and updated according to
where
- ξ -the local
evaporation factor,
- τ0 -
additional pheromone (an algorithm parameter).
After the first ant has made the kth step and has modified a pheromone, it does not begin the next step. It waits until all other ants
complete their kth steps and modify the pheromones on their traveled kth path. In this process, the n + 1 ant waits for the update by the ant n, ant and so on.
Evaporation and pheromone update
After all ants have completed iteration, pheromone update and global evaporation are
applied to paths.
In Ant Colony
Optimization for Tree and Hypertree Decompositions only the best to date
ant is allowed to update pheromone. Evaporation also is allowed only on paths
visited by this ant.
In this application, you have a
choice: the beast for iteration ant, the best to date ant, the best after reset
ant, or all ants.
The application uses equations (3)
for evaporation and (2) or (4) for the global pheromone update.
The equations are applied to paths
visited by the selected ant(s) only.
Pheromone Reset (Restart)
If ants are stuck in some local loop, there is an option to
reset all pheromones to the start values and continue run. This option might be
enabled or disabled for all implemented algorithms.
The selection threshold is
a reset parameter. If
all pheromones on paths between all cities are reset to ,
and search for the shortest path begins anew. Still, the previous history is
not destroyed. The new best to date trip updates the best after reset value; if
it is less than the global best to date trip, it also replaces the old best to
date value.
In (12)
- is
a reset parameter,
- m is the number of paths in ant's round trip,
- -
number of different edges for a current iteration between the trajectories of
the best to date and the worst for iteration ants,
- -
number of consecutive events when
,
- is
a threshold, the reset parameter.
Essentially, the reset occurs when the best to date and the
worst for iteration trajectories are very close. The user can select the action after reset: finish the run or
continue it.
If the run is to continue, the count of consecutive events resumes
from zero.
Mutation
A mutation of the pheromones on ant paths is used to prevent
the solution from getting stuck in some local loop. It is explained in the
article "Analysis of Best-Worst Ant System.." by Oscar Cordon and
others.
It seems that it was proposed for the Best-Worst Ant
Algorithm only.
In this application, the global mutation option might be
enabled or disabled for each of the implemented algorithms.
The idea is simple: you select ant paths (graph edges) at
random and increase or decrease the amount of pheromone on each of them
according to some set of rules. The rule to evaporate or increase pheromones
is:
where
- is
pheromone on the edge ,
is
a subset of paths between cities selected at random,
- is
a random value generated for each path
,
- -
add-subtract threshold, the parameter
- -
min and max limits of pheromones on paths
-
- -
mutation strength, the mutation parameter,
- -
average pheromone on path of the best to date round trip,
- -
number of current iteration,
- -
number of iteration from the last pheromone reset (see below),
- -
max number of iterations (run parameter)
The number of paths in is
calculated as
where
- -
mutation rate, parameter,
- m- number of cities
The user sets a period (interval) between mutations. In
addition, the user can set a number of resets to delay the start of the mutation
period. For example, if the number of resets is set to three and the period of
mutation is set to 30, then the application will wait for three resets to occur in
a row before it starts to count iterations for mutation.
After 30th iteration, it will execute the mutation. After
that, the application will wait for another three resets to repeat the count.
If the new reset occurs in the middle of the count, the iteration counter will be
reset. If the number of resets is set to zero, the mutations will be executed
every 30 iterations.
Pay attention to the fact that the degree of the pheromone
correction increases at the end of the test.
Travel Statistics
You can gather these statistics:
- Best for iteration and best to date trip length values at each
iteration (always is ON)
- Worst for iteration and worst to date trip length values at each
iteration
- Average over ants travel length and its standard deviation at
each iteration
- Distance - average and standard deviation of number of paths
between cities in ants round trips different from paths in the best to date
solution at each iteration
- Average and standard deviation of the branch factor - number of
paths with the quantity of pheromone deposited on them greater than some
threshold value
- Distribution of the ants start cities
- Best after reset value of round trip for each iteration
The average and standard deviation of some random variable ν are calculated as:
where
- is
an average of n variables,
- is
their standard deviation.
Distance and brunch factor need some additional explanation.
Travel Statistics: Distance
For each ant in the given
iteration, the ant's round trip is compared to the trip of the best to date
ant. Paths unique for the ant trip are counted. After that, average and
standard deviation of counts over number of ants are calculated. This
statistics is a measure of the quality of the trip: the low distance means that
either the solution is found, or we have a local loop.
But how will you count the unique
paths on a symmetrical graph? The symmetrical graph has path A->B equal to
path B->A. We decided that direction does not matter: if the best to
date ant has traveled clockwise, and the other ant traveled counterclockwise
the same trajectory, these ants traveled the same trajectory. Pay attention to
it.
Travel Statistics: Branch Factor
Let us assume we have n
cities our ants have to visit. Then each city has n-1 adjacent cities to
choose from for a next step. Each of the paths to the cities has some quantity of
pheromone deposited on it.
For each city, Branch Factor
Statistics calculates the number of paths to adjacent cities where the quantity of
the deposited pheromone is greater than some threshold. The less the count, the more
deterministic is a choice, the better is a solution.
The branch threshold is calculated
for each city separately as
where
- -
max and min pheromones on outgoing paths for the city k,
- -
parameter set by the user
Note that the branch factor takes into account all adjacent edges, no matter
if they were visited or not.
Presentation of statistics
All statistics except the start
cities are presented as linear charts. The start cities are rendered as a bar
graph.
The first two charts, the best for
the iteration and the best to date, and start cities are shown in read-only
window in the app's main dialog. The user might invoke a separate window to
analyze, save, or print all linear charts.
User Manual (Sort Of)
It is a rather long chapter, but the user interface is not so
simple.
To run some algorithm this sequence of actions should be
performed:
- Select an algorithm by name
- Select the method of city generation
- Set the cities extent that defines the range of city
coordinates
- Set the number of cities
- Set the max number of iterations
- Set parameters α,
β, and ρ (equations (1) and (3).)
- Set other algorithm's parameters if appropriate
- Enable or disable mutations and reset and set their
parameters
- Set or reset symmetry options of ant paths if
applicable
- Select statistics to gather
- Set up a trigger to get a travel graph snapshot if desired
Steps 1 - 10 might be performed in any order and many
times: the selections will be committed only after you click the 'Apply' button.
Even if the selections are committed, you still might change them if you
did not start running the algorithm.
After 'Apply' is clicked, you can run the algorithm step
by step or continuously, stop and resume the run, or cancel the run at any
moment. The algorithm parameters are locked after you start the run.
While the algorithm is running, it displays the state of the
ants' travel every 100th epoch,
at each stop and at the end of the run.
While the algorithm is running or at the stops, you can view
the charts of the gathered statistics and work with these charts in a separate
dialog box. Upon satisfaction of the trigger condition, the app will show a graph
snapshot in a separate window.
You can save a city configuration and/or a city graph structure
with its vertices and edges into XML files.
For the iteration(s) of your choice, you also can save ant
states and the underlying graphs of the solution, statistics charts, and the graph snapshot
as XML files.
At any time you can also print the report - best to date trip
data registered at that time.
All user actions and requests submitted while the algorithm
is running are performed at the end of the current iteration. After the request
is honored, the algorithm continues the run.
To change the algorithm or its parameters, you have to
cancel run (button 'Cancel') or wait to the end of the run.
Let us go to the details.
Select an algorithm
It is simple: just select an item in the 'Algorithm'
combo box.
Set cities extent, city number, max iteration number, α, β, and ρ
Use appropriate sliders. To coarse
set values use mouse, for fine adjustment use Home, End, Page Up, Page Down, and
keys.
Select the method of city generation
The application offers five methods of city
generation:
- 'Automatic Placement': the cities are placed on a circle.
The circle diameter is equal to a city's extent.
- 'Random': X and Y coordinates of cities are generated at
random; special precautions are taken to prevent generation of two cities at the
same coordinates. The distribution of the coordinate values is uniform on , where Q is the cities' extent.
- 'Manual Placement': You generate automatic or random
placement, or use the existing placement and move the cities as you need. Coordinates
of the moving city are shown in the status bar.
- 'Load Cities from File': Loads coordinates of the set
of the cities from an external XML file. You do not need to click 'Apply' to
start: go straight to 'Run'.
- 'Load Configuration from File': This option loads all
cities with their coordinates and distances between the cities as
a graph. The resulting graph acquires α,
β, evaporation factor ρ, the algorithm type, and algorithm
parameters from the user's selections in the application's main dialog window.
The initial value of pheromones is set as Q/cities number, where Q is a
city's extent. Again, you do not need to click 'Apply' to start: go straight to
'Run'.
- 'Load Graph from File': It imports the snapshot of the
algorithm's graph as it was saved at some previous epoch or many days ago: the cities,
distances between them, deposited pheromones, all things. If the graph was
saved with the charts and start city's bar graph (it is a default option at
saving graph in this app), the charts and bar graph are loaded too. You might
continue from the iteration (epoch) the graph was saved. To use only the
configuration, you have to select 'Use existing configuration' and reapply it.
Again, you do not need to click 'Apply'.
- 'Use existing map': It uses what city's configuration was generated last or loaded.
The options Load Configuration from File and Load Graph from File are using the distances between
cities as they were saved in the corresponding XML files. All other options
automatically calculate the distances between the generated or loaded cities as
Euclidean Distances.
Manually Setting Cities
As was mentioned above, you can manually
set any city configuration you want by using Manual Placement. The
only constraint is all Xs and Ys must be non-negative. It
is recommended to set all other algorithm parameters before you start the
manual placement, because the configuration you would set will be committed
automatically. Of course, you can set any parameter after you have done with
placement with Use existing map.
To do manual placement:
- Set the sliders 'Cities Extent' and 'Number Of Cities'
to values you need.
- Select 'Manual Placement' in 'Cities/Method of Generation'
combo box. The dialog box will be displayed to select the method of cities
generation. Select 'Automatic', or 'Random', or 'Using Existing Map', and click 'OK'.
- The generated cities configuration will be displayed in the main
app dialog box's picture control. Select the city with left mouse click
and drag the city with mouse or using the arrow keys to the position you
want.
The city's name and coordinates are displayed in the first pane (pane 0)
of the
status bar of the dialog box. You also can invoke a city label by
right-clicking
on the city.
- When you are done, double left click on the button OK in
the picture control. The configuration will be committed, and you can start
running.
Remember that the distances between
the cities will be automatically calculated as Euclidean distances. If your
distances are supposed to be different, see next paragraph.
Setting arbitrary cities configuration and distances (committing city map)
Distances between cities are used
in calculations only, so you can set any distance value convenient to you. Be
realistic and remember that the shortest possible distance between cities is
the Euclidian distance.
Suppose you have a map of places
you have to visit, with one-way streets between them. It means that sometimes a
distance between places A and B is not equal to the distance between B and A.
Still, you can work with your map in this app using an XML configuration file to
set the map and load it into the application.
To set an arbitrary cities
configuration, you have to generate some start configuration, save it into an
XML file, change the file, and load it back.
First, you have to generate a city
configuration for your cities extent and number of cities. Any generation
method ("Regular', 'Random', or 'Manual') is good. Commit the
configuration by clicking on Apply. After that go to the
Options/Save/Save Configuration submenu item, click on it, and save the configuration as a
configuration graph XML file.
Now open the file in any XML editor
(I recommend Microsoft
XML Notepad 2007, it is free and good, but you can use MS Visual Studio or
anything that works). You will see something like this:
<Config_Graph>
<Graph_Prop CitiesNum="10" SymMut="true" SymDist="false" StartPher="0.1" CitiesExtent="25"/>
<Vertex ID="0" Name="City_0" X="8.536407" Y="3.749408">
<Edges>
<Target ID="1" Name="City_1" X="2.025207" Y="9.906549" Dist="8.9613676071167"/>
<Target ID="2" Name="City_2" X="0.2259159" Y="0.8545399" Dist="8.80025672912598"/>
<Target ID="3" Name="City_3" X="11.42984" Y="5.034723" Dist="3.16607141494751"/>
<Target ID="4" Name="City_4" X="11.51926" Y="7.236289" Dist="4.58865690231323"/>
<Target ID="5" Name="City_5" X="6.953999" Y="7.392624" Dist="3.97203135490417"/>
....................................................................................................
</Edges>
</Vertex>
<Vertex ID="1" Name="City_1" X="2.025207" Y="9.906549">
<Edges>
................................................................................................................
Change the city names,
coordinates, and distances between cities according to your map. If distance
(A, B) ≠ distance (B, A) for some pair of cities, change SymMut and
SymDist to
false (I will explain it later.) SymMut
must be true for a symmetrical map, where distance (A, B) ≠ distance (B, A) for
all cities. Save the file, return to or start the app, and load the
configuration.
By default, cities have names like 'City_0',
'City_1', etc. Apply the same procedure to the cities or configuration
XML files to change the city names.
Set other algorithm
parameters
Click on 'Edit Ant Options'. The
appropriate dialog box will be displayed if there are additional algorithm
parameters. Select parameters and click OK. If you call this dialog box and
do not want to change previous settings, click Cancel. For example, this is a
dialog box to set the number of ranked ants and their evaporation factor for
Ranked Ants algorithm.
Enable or disable mutation and/or reset and set their parameters
Click the Options menu
button and click the Mutation or Reset menu item. Set parameters in
dialog boxes displayed and click OK. If the checkbox 'Allow' in the dialog
boxes is unchecked, all other controls of the box are disabled, do not try to
change their state then. This is the mutation parameters dialog box:
Some parameters need explanation (see equations (13)):
- 'MUT PERIOD' - period of mutations, might be set between 1
and 100 epochs
- 'SEL THRESHOLD' - the threshold between decreasing and
increasing mutations
- 'MUT RATE' - a fraction of the graph edges subject to
mutation
- 'WAIT FOR RST' - number of resets before start of
mutations; could be zero; if the reset is not enabled, the slider is disabled
- 'MUT STRENGTH' - fraction of calculated full mutation to
apply to edges
For Reset, there are only
two parameters: the fraction of graph edges unique for the worst ant for
the current iteration compared to the best to date trip to invoke the reset, and a number of successive repetitions of
this event to reset the travel. There also is a list box to select the actions upon
reset. The actions are:
- No Pheromone Reset: This action is used together with mutations:
if mutations are enabled and Wait for Rst not zero,
instead of resetting all graph edges to the start pheromone, the application
will mutate pheromones after a set number of resets occur.
- Reset: Upon reset, all pheromones are reset to the start
value.
- End Run: Pheromones are reset and test is finished. The
user might continue this test or start a new test.
Set or Reset a Symmetrical Option
If the distance between cities A
and B is not equal to the distance between B and A, the cities graph is
asymmetrical. You have to calculate pheromones on each edge of the graph
separately.
If d (A, B) == d (B, A), there
are two options. You may assume that the route between A and B has two separate
one-way lanes and calculate pheromones for each lane separately, or assume that
there is one two-way lane, and just set the pheromone on edge B, A equal to
pheromone on edge A, B. You have a choice for the symmetrical graph to set one
of these options: click the Options menu button and click on the Symmetrical
Paths menu item.
The only way to set different distances
is via Configuration XML (see Setting arbitrary cities configurations above).
Select Statistics to Gather
There are statistics you can
gather:
- Best for iteration and best to date travel values for each
iteration (always ON)
- Worst for iteration and worst to date travel values for each
iteration
- Average travel length and its standard deviation for each
iteration
- Average and standard deviation of number of paths in ants round
trips different from path in the best to
date solution for each iteration
- Average and standard deviation of the branch factor: number of
paths for that quantity of pheromone
deposited is greater than some threshold value
- Distribution of the ants' start cities
- Best after reset value of round trip for each iteration
To enable or disable statistics,
click on the Options menu button, click the Set Statistics &
Results menu item, and select the desired set of statistics. Use the slider to
set the Branch Factor threshold.
For every statistics ('Start
Cities' excluded) the collected data is represented as linear charts.
Run the Test
To commit all parameters, click on the Apply
button. The buttons Run and Step are enabled after that.
You can go step by step or run the
test continuously and stop the run at any moment. To switch from running to
step-by-step you have to stop the run first. To resume the run after stop, you
have to click on the Stop button again (capture is changed to 'Resume')
after stop.
While the test is running, all
controls which allow changing the algorithm, algorithm's and test's parameters,
are disabled. You have to wait until completion of the test or interrupt it at
any moment with a click on the button Cancel Run. This action only cancels
the mode; all parameters are not changed or deleted. You can continue the test
with Run or Step from the point you have canceled the test or
change the algorithm and/or parameters and click Apply to clear old
parameters and data and start with a new set of parameters. Until the new
settings are committed, all previous test data are accessible. You can monitor
the test's progress all the time until a new algorithm and/or algorithm's
parameters are committed.
Monitoring the test
Every 100 iterations and on each stop the application updates its data and
displays the trip's length and its trajectory for the current epoch. It also provides
trip lengths for the best and worst ants for the current iteration, best trip
after the last reset, and best and worst to date results. You select the ant
from the combo box and see an epoch, an ant's ID, and trip length in the control
to the left of the box. The trip trajectory is shown below the box.
The statistics are also updated on
100th iterations, on each stop, on completing or canceling the run.
Statistics charts for the best for
each iteration and the best to date trip length are shown in the main dialog. This
chart control is read-only; that means that no user input is enabled. To see
all charts and interact with them (e.g., hide, pan, zoom, save, etc.) you have
to select View Charts from Options. This action will
display the Chart control.
To get a full grasp of the chart
control features you better read my article
An MFC Chart Control with Enhanced User Interface but here is a short
version of its user's manual:
- To see chart values, enable tracking by a mouse middle button
click (the cursor will change its shape to a cross). After that select the
X-coordinate and left click on the chart to see the data legend for the
selected X.
- To zoom horizontally, select the zoom boundaries with SHIFT + left
click.
- To zoom vertically, select the first zoom boundary with the SHIFT
+ left double click and the second boundary with SHIFT + left click.
- To pan horizontally use left and right arrow keys or SHIFT + mouse
wheel.
- To pan vertically use UP and DOWN arrow keys.
- To change the Y scale for a selected chart, first select is with
CTRL + left click, after that use CTRL + mouse wheel or up/down keys to change
the Y-scale
- All other actions on charts, like hide/show, save, print, are
allowed from the popup menu that is displayed on the right mouse click on the
chart control.
The size of this chart control
window might be changed by the user.
The algorithm continues to run
if it was not stopped by the user. To update the charts in this control you
have to click View Charts again.
At any moment, you can print the
data for the best to date travel for this epoch by selecting the 'Print
Report' item from the menu button 'Options'. You will present with
MFC Print Dialog to select printer, printer setting, and print options. The
report consists of several pages. The first page shows the best to date trip
data (travel length, epoch, etc.), the algorithm info, and the picture of the trip
trajectory like shown above. Other pages show the best to date trajectory as a
table. One page of the table shows approximately 40 rows.
If you select 'Selection' in the
print dialog, only the first page is printed. Otherwise the full report is
printed. To get more flexibility you can install some converter to print the
report to a pdf file (like doPdf, it is free and very good) or print to MS XPS
file.
The last and, might be, the most
important feature of this app (I did not see it in other Ant Colony apps) is a
possibility to set a trigger point and get a system snapshot at this point. The
trigger might be set at any time after the algorithm is committed. From the 'Options',
select 'Graph Snapshot Settings'. You will see the 'Triggers for
Graph Snapshots' dialog box.
It is self-explaining; only two
check boxes need additional mention. The first is Continue Run. By
default, the trigger interrupts the test run, and the user must click 'Resume'
button to continue the test. If this box is checked, the run will continue.
The second is 'Renew...'
Again, by default, the trigger is cleared after a triggering event occurs. When
the box is checked, the trigger will reset. For example, if the trigger is set
for 'Best to Date Change', you will continuously receive snapshots each
time the best to date travel distance is changed. The triggers must be set only
after the test parameters are committed, because a click on the button 'Apply'
resets them to no trigger mode.
Upon the trigger event, the edges
dialog box is displayed. It shows the graph edges
originating from some source vertex (a city.) You can change the source city by
selecting the new city with left mouse button click on it. You can choose the
target vertex for this source city (the target city) with CTRL + left click. A
right click on a city will invoke the tool tip window with the city's name. The
second right click on the same city will hide the name. The right click on the
white space will hide all tooltips.
Text boxes to the right of the edge
picture control show main algorithm parameters, data on the selected ant, and
data on the source and the target cities and an edge connecting them. The
legend for the edge colors is below the edge picture control.
A click on the 'View Ant Graph'
will show an edge view of the snapshot. It has
many pages. The first page is a selected (in the previous dialog) ant's travel
trajectory. The other page show edges for all source cities; each source city
has a separate page. The table shows the target, the distance from the source, the
edge pheromone before the ant choose a next edge to travel, probability of choice,
and the pheromone after update at the end of the trip.
To navigate between pages, use the
buttons at the bottom of page. You also can select the source city by left
click on the city on the first page. You also can follow the ant's trip by
selecting the start city on the first page, and clicking on the target city
circle on the next pages.
If a page cannot display all edges
for the given source city, you may scroll the page with UP/DOWN keys if the
page has focus (click on page to set it.)
You can save all tables for all
source cities into an XML file. You can also print the all tables, the table
for the selected source city, or any number of source cities. Keep in mind that
the printing of all ten-city sources will take 11 paper pages; for 100 cities it
will take 301 paper pages.
Saving results in XML files
There are five options to
save data in XML files:
- Save Cities: Saves ID, names, and coordinates of generated
cities.
- Save Configuration: In addition, saves distances between cities
- Save (Colony) Graph: Saves entire system graph with cities ID, names,
coordinates; distances between the cities and volume of pheromone on edges for
the epoch the data are taken. The algorithm parameters, mutation and reset
parameters, type of gathered statistics are also saved. Also saved are ants'
trip trajectories for the given epoch. In addition, the epochs, edge
pheromones, and traveled state are saved for the best for last iteration, best
to date, best after reset, worst for last iteration, and worst to date ants.
Charts and start cities distribution are automatically saved in separate files
- Save Colony Ants: Saves trip trajectories for all ants
- Save Charts: Saves statistics' charts
All options are accessible
from 'Options/Save'.
In addition, you can save the
selected ant's graph from the Edge View dialog, and save charts from a chart
control's popup menu.
The cities and configuration
might be loaded back to the application via the combo box 'Method of
Generation' to run with any registered algorithm. The cities XML file
allows modifying cities coordinates and names of the cities before loading the
file back. Distances between the cities the application will calculate as
Euclidian distances.
The configuration file allows
changing the distances between its cities in addition to the cities coordinates
and names.
The colony graph XML file
encapsulates a full system snapshot at the epoch the saving operation was
requested. Actually, it might be three XML files: the graph itself, with
algorithm, its parameters, and statistics requested, a charts XML file if the
charts have data (if the epoch at saving the graph was greater than zero), and a cities
bar graph if the start cities statistics was requested and gathered. This is
why I recommend organizing some common folder to keep all three files. You set
the name of the graph file only; the chart and cities files are named
automatically. For example, if the graph file is named 'TestB.xml, the chart
file will have name 'TestB_Charts.xml', and the cities file is
'TestB_CitiesChart.xml'.
If you choose to load the colony
graph XML file, the files for charts and cities will be loaded automatically if
they exist. After the file(s) are loaded, you can run the test from the epoch
the colony graph was saved. If you have lost the chart file the application
will gather and calculate statistics beginning from the loaded epoch. The same
is true for the start cities distribution.
Upon receiving a request to
save into an XML file, the application displays MFC CFileDialog dialog box. You
are free to select any place to save the file. To introduce some order in this
process, I set default subfolders for each type of data in the AntCol working
directory to keep the files, so the CFileDialog opens at the default subfolders
for each type of the data to save if you set these subfolders. The subfolders
are:
- Cities
- ConfigGraphs
- Graphs
- Ants
- Charts
- AntGraphs
It works as follows:
- The application gets the full module name of AntCol.exe like "C:\...\AntCol.exe".
- It strips the module name of the
file name (AntCol.exe).
- It searches the module path for a
subdirectory "AntCol".
- It erases all characters after "AntCol", adds the back slash after "Col", and adds the
folder name from the list, depending on what the user wants to save.
- It passes the resulting path to
CFileDialog as a default path, so the dialog starts in this path. - If the folder AntCol is not found,
CFileDialog will
start in the MyDocument
directory.
You have to set your working
directory as ".....\AntCol" and copy the executable file AntCol.exe
into it. After that, you have to create these subfolders in the working
directory AntCol.
Of course, you can live
without all this stuff and keep saving the XML files in any place on your
computer or your network.
What is under the hood, or points of interest
This application is a dialog-based MFC application with
heavy use of Boost Graph Library and GDI+.
Its main class, CAntColApp is derived from MFC extension
class CWinAppEx.
If you do want to peruse the app code, there are four
functions to start with:
All these functions are in the files AntColDlg.h, AntColDlg.cpp.
From there you can travel to other functions called from inside, and the
functions these secondary functions called, and so on and so forth.
Model
The natural math model of the Traveling Salesman Problem is
a graph: vertices are cities, and edges are routes between the cities. Each
vertex is connected to all other cities. In the Boost Graph Library, this model is
best described by a directed adjacency list graph. To connect algorithm
parameters, cities, and routes between cities to the graph, I have provided bundled
properties for the graph itself, its vertices, and edges. The properties are
defined in the file Colony.h.
The Graph property is:
struct AntColProp
{
..............................................................
bool m_bSymMut; bool m_bSym; int m_grID; int m_startIdx; double m_startPher; double m_alpha; double m_beta; double m_evap; float m_citiesExtent; string_t m_szAlgName; };
Here string_t stays for std::basic_string<TCHAR>.
In the directed adjacency list the edge connecting vertices i and j is not equal to the edge connecting
j and i. However, more
often than not, a route connecting any two cities is bidirectional. The property
members m_bSymMut and m_bSym are the flags signaling that additional care
should be taken of the symmetrical edges ij and ji to make edge
length and pheromone equal. For an asymmetrical graph, m_bSymMut
is always false and value of m_bSym does not matter. For
a symmetrical graph,
m_bSymMut = true, and
for bidirectional routes m_bSym must be true. You can try to process edges in the symmetrical
graph as asymmetrical by setting m_bSym = false.
The structure also includes a constructor and a function string_t GetAntColPropStr(int citiesNum) to translate member values into string.
A problem with access to the
adjacency graph bundled property was reported earlier. The solution is to call
boost::get_property(graph&, graph name) which is different from dealing with other bundled
properties.
The vertex property is:
struct City
{
......................
int m_idx;
string_t m_szName;
bool m_bVisited;
Gdiplus::PointF m_pntLocationF;
};
By default, upon placement of cities, the cities get names
like "City_0", "City_1", etc. Cities names can be changed
outside the application and the entire configuration loaded back. The user can set
the extent of the square that contain the cities from 1.0 to 100.0.
The edge property is:
struct Path
{
..............................
bool m_bTraveled;
double m_dist;
double m_pher;
};
By default the edge length (the distance between two cities),
m_dist, is calculated as:
Again, there is an option to change the edge length out of
the application. Because m_dist is used for calculation only, it might have any value.
Here is the definition of the Traveling Salesman's graph:
typedef adjacency_list<vecS, vecS, directedS, City, Path,
property<graph_name_t, AntColProp> > GRAPH;
Information about this class can be got from the Boost::adjacency_list web page.
I am aware that the STL lists are not the best structure for search,
but in the Release configuration and one hundred cities, the app
performance is not so bad.
Classes
There are three main players in this application: the
classes CAnt,
CColony,
and the hierarchy of algorithm classes.
CAnt (Colony.h) is just storage to keep all things the ant needs for graph navigation:
class CAnt
{
..............................................
public:
int m_antID;
GRAPH m_antCitiesGraph;
std::list<City> m_lstAntPath;
double m_travelLength;
vertex_descriptor m_currVertex;
vertex_descriptor m_startVertex;
int m_epoch;
};
CColony (Colony.h) is charged with some tasks to process
and keep results of ant trips and some tasks on a set of ants.
class CColony
{
................................................................
public:
static std::mt19937 m_rndGenAnts; static std::mt19937 m_rndColony;
static const int m_antNmb; MAP_ANTS m_mapAnts;
GRAPH m_colGraph; int m_startRstEpoch; int m_rstNmb; int m_maxRun;
};
The main dialog has a member m_antColony. Before each trip, the colony passes the colony graph to its ants. The ant trajectories are saved in
m_lstAntPath for each ant, and the colony graph is updated
according to the trip trajectories. All ants are kept in a map
m_mapAnts.
We will discuss algorithm classes later.
How it works
The user chooses an algorithm, its parameters, number of cities and
number of trips, and a method of city generation. He/she also selects
the statistics to gather. After that,
the user commits the selections by clicking on the button Apply.
The application calls the
algorithm factory to instantiate the chosen algorithm and the statistics
factory to compile the map of statistics. It also enables/disables the appropriate
UI controls.
After that, the user clicks Ran or Step, and the application starts the worker thread to run the algorithm.
The application controls interaction between the main thread
and the worker with four event handles (files AntColDlg.h and AntColDlg.cpp):
HANDLE m_hEvAbortRun;
HANDLE m_hEvStopReq;
HANDLE m_hEvInfoReq;
HANDLE m_hEvContRun;
The handle names are self-explaining (more details follow). The
events control the wait function in the worker thread. After the worker
thread exits or is interrupted by these
events, the user might resume the run or change an algorithm and/or
algorithm
and test's parameters.
The algorithm classes
All algorithm classes (files TravelAlg.h and TravelAlg.cpp) are
derived from the base class CASTravelBase. All new algorithm classes must
be derived from this base class. The class defines the algorithm interface:
class CASTravelBase
{
public:
CASTravelBase();
virtual ~CASTravelBase();
virtual unsigned int TravelGraphOnce(CColony& antColony) = 0;
virtual void UpdateASGraphOnce(CColony& antColony) = 0;
virtual string_t GetAlgName(void)const = 0;
virtual void GetAlgParams(V_ALGPARAMS& vAlgParams) = 0;
virtual string_t GetAlgParamStrT(void) = 0;
virtual void SetAlgParams(V_ALGPARAMS& vAlgParams) = 0;
static void GetMutParams(V_ALGPARAMS& vAlgParams);
static string_t GetMutParamStrT(bool bShort = true);
static void GetRstParams(V_ALGPARAMS& vAlgParams);
static string_t GetRstParamStrT(bool bShort = true);
static void SetMutParams(V_ALGPARAMS& vAlgParams);
static void SetRstParams(V_ALGPARAMS& vAlgParams);
virtual string_t GetParamString(void) {return string_t(_T(""));}
RST_ACTIONS RestartAlgorithm(CColony& antColony);
void MutatePheromones(CColony& antColony);
protected:
void EvaporateEgdePheromones(CColony& antColony, double evapFactor);
void TravelGraphOnce(CAnt& ant);
void UpdateAntPathPher(GRAPH& colGraph, CAnt& ant);
void UpdateAntPathPher(GRAPH& colGraph, CAnt& ant, double multiplier);
public:
static CDlgMut* GetMutDlg(bool bDelete = false);
static CDlgRst* GetRstDlg(bool bDelete = false);
virtual INT_PTR RunDlg(void)
{
AfxMessageBox(_T("There are no additional alg params"));
return IDCANCEL;
}
static void DeleteParamsDlgs(void);
public:
static double m_mutMinPher; static double m_mutMaxPher; static bool m_bMutAllowed;
static bool m_bRstAllowed;
static int m_mutPeriod;
static double m_mutRndTrsh;
static double m_mutRate;
static double m_mutStrength;
static int m_mutRstTrsh; static int m_mutRstCnt; static int m_rstTrsh;
static int m_rstCntTrsh; static RST_ACTIONS m_rstAction; static string_t m_strMutAllowed;
static string_t m_strMutMinPher;
static string_t m_strMutMaxPher;
static string_t m_strRstAllowed;
static string_t m_strMutPeriod;
static string_t m_strMutRndTrsh;
static string_t m_strMutRate;
static string_t m_strMutStrength;
static string_t m_strMutRstTrsh;
static string_t m_strMutRstCnt;
static string_t m_strRstTrsh;
static string_t m_strRstCntTrsh;
static string_t m_strRstAction;
static string_t m_strActions[];
};
Strictly speaking, only TravelGraphOnce and UpdateASGraphOnce implement an algorithm itself. All other
virtual functions define interactions between the application, the user, and
the algorithm.
Generally, all the algorithm must know is its parameters α, β, and evaporation
factor ρ (see eq. 1 and 3). It needs them to calculate probabilities
of transition to the next city and evaporate pheromones. The algorithm receives
these parameters from the colony instance, as the colony graph's properties.
Other parameters, if there are any (e.g., number of ranked
ants for Ranked Ants Algorithm, or local evaporation factor for Ant Colony) the
algorithm should get from outside. In this application, the user sets these
additional parameters from the appropriate dialog boxes. The dialog boxes are separate
classes, but the algorithms (the user) might invoke them using the virtual function
INT_PTR RunDlg(void).
This function just calls DoModal on the appropriate dialog class.
The dialogs do not have their own data members; they use data
members of the corresponding algorithms. All algorithms' additional parameters are
declared static, so they are accessible any time. On OK,
the dialog box reads the state of its controls and sets the appropriate algorithm's
static data members.
Each additional algorithm's parameter has a counterpart, its
name, a static string. We need the names to facilitate exchanges between
XML files and algorithm parameters. We have introduced the virtual functions
GetAlgParams(V_ALGPARAMS & vAlgParams) and SetAlgParams(V_ALGPARAMS& vAlgParams). The vector
V_ALGPARAMS is a vector of pairs
std::pair(bstr_t (parameter
name) ,variant_t (parameter value))
. Using
bstr_t and
variant_t allows to have
the same type of vector elements for different types of values (e.g.,
float,
int,
bool, etc.)
Finally, to render the algorithm state in a legible form,
there are the virtual functions GetAlgName, GetAlgParamStrT,
GetParamString. The last
function is used to set text in the static control of the main application
dialog.
The class CASTravelBase also includes
static functions to set and get parameters of mutation and reset modes. We have
mentioned before that mutation and reset modes might be set by the user for any
algorithm, therefore the functions
RST_ACTIONS
RestartAlgorithm(CColony& antColony)
and
void MutatePheromones(CColony& antColony) are made members of the base class.
To show how the algorithm interface is defined for some
concrete algorithm, I will show the class for the Elitist Ant Algorithm:
There is a class for the Elitist Ant Colony Algorithm
derived from CASTravelBase:
class CASETravel:public CASTravelBase
{
public:
CASETravel(void);
virtual ~CASETravel(void);
static CASTravelBase* CreateASETravelAlg() { return new CASETravel;}
virtual unsigned int TravelGraphOnce(CColony& antColony);
virtual void UpdateASGraphOnce(CColony& antColony);
virtual string_t GetAlgName(void) const {return AlgName();}
virtual void GetAlgParams(V_ALGPARAMS& vAlgParams);
virtual string_t GetAlgParamStrT(void);
virtual void SetAlgParams(V_ALGPARAMS& vAlgParams);
static bool RegisterWithFactory(void);
public:
virtual CString GetParamString(void);
private:
unsigned int TravelASEGraphOnce(CColony& antColony);
void UpdateASEPheromone(CColony& antColony);
string_t AlgName(void) const {return m_szAlgName;}
public:
static CDlgEAS* GetMnDlg(bool bDelete = false);
virtual INT_PTR RunDlg(void) {return GetMnDlg()->DoModal();}
static void DeleteParamsDlgs(void);
public:
static double m_easFactor;
static string_t m_strEasFactor;
public:
static const string_t m_szAlgName;
...................................................................
};
You can see an implementation of this class in TravelAlg.cpp.
Algorithm factory
To get instances of algorithms I am using the algorithm
factory. It is implemented as a Scott Meyers Singleton:
CTravelAlgFactory& CTravelAlgFactory::Instance()
{
static CTravelAlgFactory factory;
return factory;
}
I know about problems with Singleton in multithreading
applications. In this application, the worker thread never ever tries to
instantiate an algorithm. Instead, it receives the pointer to the algorithm
instance from the main thread.
To register the algorithms with the factory I am using a std::map with algorithm names as keys and algorithm creator functions as
values. It means that the algorithm must have a unique name for this application.
Each algorithm has a static creator member function, for
example:
static CASTravelBase* CreateACSTravelAlg() { return new CACSTravel;}
To register an algorithm, the algorithm factory has the function:
bool RegisterCreatorAlgFn(const string_t& algName, TravelAlgCreator creatorFn)
{
bool bResAlg = m_algMap.insert(MAP_TRAVELALG::value_type(algName, creatorFn)).second;
if (bResAlg)
m_vAlgNames.push_back(algName);
return bResAlg;
}
The vector m_vAlgNames is used to initiate a combo box of algorithm names (we will discuss it later).
Each algorithm calls this function to register itself. For example:
bool CACSTravel::RegisterWithFactory(void)
{
return travelAlgFactory.RegisterCreatorAlgFn(m_szAlgName, CreateACSTravelAlg);
}
If some other algorithm was registered under the same name,
the insert function will fail, and the register function will return false.
To register all algorithms in a given application and to have the possibility
of easy addition of new algorithms to the application I use TypeLists to enumerate and register all algorithm classes with the factory.
Using TypeLists for algorithm registration
The code for TypeList templates is in the file TypeLists.h.
Andrei Alexandrescu in his book "Modern C++ Design"
has defined TypeList as a template.
template <class T, class U>
struct TypeList
{
typedef T Head;
typedef U Tail;
};
It is a very simple template, but it is amazing what you can accomplish with it.
In the book and in the Loki library (Loki\MSVC\1300\Typelist.h)
there are macros to define TypeLists for sets of classes:
#define TYPELIST_1(T1) TypeList<T1, NullType>
#define TYPELIST_2(T1, T2) TypeList<T1, TYPELIST_1(T2)>
#define TYPELIST_3(T1, T2, T3) TypeList<T1, TYPELIST_2(T2, T3)>
#define TYPELIST_4(T1, T2, T3, T4) TypeList<T1, TYPELIST_3(T2, T3, T4)>
#define TYPELIST_5(T1, T2, T3, T4, T5) TypeList<T1, TYPELIST_4(T2, T3, T4, T5)>
#define TYPELIST_6(T1, T2, T3, T4, T5, T6) TypeList<T1, TYPELIST_5(T2, T3, T4, T5, T6)>
..........................................................................................
Loki library defines macros up to 50 classes, but you can
get an idea from these defines. In the Loki library there is a template
MakeTypeList that automatically generates TypeList up to 18 data types.
To automate the registration of algorithms, we are using a
template RegFactoryClasses (file TypeLists.h):
template <class TList, int idx>
struct RegFactoryClasses;
template <class Head, class Tail>
struct RegFactoryClasses<TypeList<Head, Tail>, 0>
{
typedef Head Result;
static inline void Fn(void)
{
Result::RegisterWithFactory();
}
};
template <class Head, class Tail, int idx>
struct RegFactoryClasses<TypeList<Head, Tail>, idx>
{
typedef typename RegFactoryClasses<Tail, idx - 1>::Result Result;
static inline void Fn(void)
{
Result::RegisterWithFactory();
RegFactoryClasses<TypeList<Head, Tail>, idx - 1>::Fn();
}
};
The compiler at compile time begins unwinding the
template, each time calling the static function Head::RegisterWithFactory(),
where Head is some class from the TypeList. The compiler stops at index
zero.
So we need to define our TypeList for six algorithms now
in the application:
typedef TYPELIST_6(CASTravel, CASETravel, CRASTravel, CBWASTravel, CMMASTravel, CACSTravel) AlgTypeList;
Also we typedef our structure RegFactoryClasses:
typedef RegFactoryClasses<AlgTypeList, TypeListLength<AlgTypeList>::value - 1 > RegAlgStruct;
Here TypeListLength is a meta-function also defined in Andrei's book:
template <class TList>
struct TypeListLength;
template <>
struct TypeListLength<NullType>
{
enum {value = 0};
};
template < class T, class U >
struct TypeListLength<TypeList<T, U> >
{
enum { value = 1 + TypeListLength<U>::value};
};
Now it is elementary: in OnInitDialog() of the main dialog,
you call:
RegAlgStruct::Fn();
It starts calling the algorithms' RegisterWithFactory functions beginning from the last type in
the TypeList, CACSTravel. In the process of registration, the creation functions of
the algorithms are being added to the map of the registered algorithms with
algorithm names as keys. Because the map is a sorted container, the order of
keys in the map is not immediately clear.
We are presenting algorithm types for the user selection in a
combo box of the main dialog, and we want the box to show them in the same
order they appear in the TypeList at the time of
registration. Therefore,
at the time of registration, we add the algorithm name to the vector of
strings. The vector is a data member of the algorithm factory. Later, we
initialize the combo box using this vector, not worrying about the
number
and names of algorithms. Because the first class in the TypeList is registered
last, we start from the end of the vector:
V_ALGNAMES::reverse_iterator rIt = CTravelAlgFactory::m_vAlgNames.rbegin();
V_ALGNAMES::reverse_iterator rItE = CTravelAlgFactory::m_vAlgNames.rend();
for (int idx = 0; rIt != rItE; ++rIt, ++idx)
{
m_comboAlg.InsertString(idx, rIt->c_str());
}
I have mentioned earlier that additional algorithm parameters
are being set via dialogs. The dialogs are created on heap. To free the memory upon
destruction of algorithm, we are using the TypeList again. It is the template
(file TypeLists.h):
template <class Head, class Tail, int idx>
struct DestroyParamsDlgs<TypeList<Head, Tail>, idx>
Statistics
Again, there is a hierarchy of statistics, all derived from a base class (file TStat.h):
class CTStatBase
{
public:
CTStatBase(void);
virtual ~CTStatBase(void);
public:
void UpdateDataCapacity(size_t maxRun);
virtual int TravelStatID(void) const = 0;
virtual V_CHARTNAMES* ChartNames(void) = 0;
virtual void InitStatParams(void) {};
virtual void CalculateDataSample(const CColony& antColony) = 0;
virtual size_t ExportData(CChartContainer& chartContainer, int initEpoch) = 0;
public:
V_STATDATA m_vData1; V_STATDATA m_vData2;
};
All statistics data are stored in two
std::vector<double> data members, m_vData1 and
m_vData2. What exactly is stored depends on the type of
statistics. For example, for Best to date and Best per
iteration statistics are
length of travel for the best to date and best for iteration ants.
To optimize the use of memory, we use the function UpdateDataCapacity(size_t maxRun). It reserves the memory for the vector exactly to
maxRum
elements.
The key function here is CalculateDataSample. It is called upon completion of one
trip.
The statistics data are presented to the
user as numbers and charts. The number of charts per statistics varies. For
example, the Distance statistics has three charts: an average distance, and average
± standard deviation charts. The names of
the charts are stored in the vector of chart names that is a data member of the
concrete statistics.
Upon the user or application's request, the function ExportData
takes the accumulated chunk
of data, calculates data for the charts, and appends charts. It happens
every 100 trips, or on each stop, and on completion of the test.
The statistics classes are:
CTStatBest: gathers travel lengths for best to date and best for iteration antsCTStatWorst:
travel lengths for worst to date and worst for iteration antsCTStatLength: average and standard deviation of lengths
of ant trips for current iterationCTStatDist: average and standard deviation for distances for current iteration (see
Travel Statistics above)CTStatBranch: the same for branching (see Travel Statistics)CTStatCities: distribution of start citiesCTStatRst: intervals between consecutive resets, if the resets are enabled
This is an example of a concrete statistics class:
class CTStatBest : public CTStatBase
{
public:
CTStatBest(void);
virtual ~CTStatBest(void);
public:
static CTStatBase* CreateTStatBest() { return new CTStatBest;}
virtual int TravelStatID() const {return m_statID;}
virtual V_CHARTNAMES* ChartNames() {return &m_vChartNames;}
virtual void CalculateDataSample(const CColony& antColony);
virtual size_t ExportData(CChartContainer& chartContainer,
int initEpoch);
static bool RegisterWithFactory(void);
public:
static const int m_statID;
V_CHARTNAMES m_vChartNames;
};
You can see the implementation in the file TStat.cpp.
Again, we are using the class factory and TypeList to
register the statistics with the factory:
typedef TYPELIST_7(CTStatBest, CTStatWorst, CTStatLength, CTStatDist,
CTStatBranch, CTStatCities, CTStatRst) TStatList;
typedef RegFactoryClasses<TStatList,
TypeListLength<TStatList>::value -1> RegTStatStruct;
As you can see, there are seven statistics, and RegFactoryClasses uses
TStatList, not AlgTypeList.
The trick is, the statistics classes also have static
functions named RegisterWithFactory, so there is no need to overwrite the definition of
RegFactoryClasses.
Besides, we are using TypeList to
initialize a static data member m_statID of a Statistics class. For example:
const int CTStatBest::m_statID = IndexOf<TStatList, CTStatBest>::value;
IndexOf is the structure defined by Andrei Alexandrescu:
template <typename T>
struct IndexOf<NullType, T>
{
enum { value = -1};
};
template <class Tail, typename T>
struct IndexOf<TypeList<T, Tail>, T>
{
enum {value = 0};
};
template <class Head, class Tail, typename T>
struct IndexOf<TypeList<Head, Tail>, T>
{
private:
enum {temp = IndexOf<Tail, T>::value};
public:
enum {value = temp == -1 ? -1 : 1 +temp};
};
TypeList and IndexOf together replace enum values.
Lambda expressions, STL algorithms, and this application
In this application, we often use STL algorithms like std::transform,
std::minmax_element, std::for_each, etc. Often we are applying these
algorithms to containers that keep some structures. To process the data, the STL
algorithms need some predicates or functions to be supplied because operations
like less_than or greater_than are often not
defined for these structures. C++ lambda expressions come to rescue here.
For
example, a code snippet below calculates the maximum value of cities
coordinates to get cities' extent, the square that envelops all cities (file AntColDlg.cpp):
float CAntColDlg::GetCitiesExtent(const MAP_CITIES& mapCities)
{
float maxCoord = 0.0f;
for_each(mapCities.begin(), mapCities.end(),
[&maxCoord](const PAIR_CITY& pair_city) ->void
{PointF pntF = pair_city.second.m_pntLocationF;
float locM = max(pntF.X, pntF.Y);
if (maxCoord < locM) maxCoord = locM;});
....................................................
}
It is an example of a lambda expression with the capture
clause.
First, we define the range of iterators to operate on (it
is the entire map of the cities).
Second, we define a local variable maxCoord = 0.0f.
Next, we call the algorithm for_each on iterators range. The
lambda expression defines the calculations we are going to do.
The variables in the square
brackets are captured variables. VS 2012 Help says: "The lambda expression
can access any variable that has automatic storage duration and that can
be accessed in the enclosing scope." It is a
very powerful feature of lambda expressions.
If the lambda expression is going
to change a value of the captured local variable, you have to pass it by
reference.
Next is a parameter list. As it is
usual for STL algorithms, it dereferences the container iterator.
->void is an expression's return type. That method of declaring
the function return type is introduced in C++ 11 standard.
And finally, there is a body of
the expression.
We access the member of the City, m_pntLocationF, select the maximum of its coordinates X or Y, and update the
captured local variable maxCoord if needed.
In the code,
you find the lambda expressions used with std::transform and other STL
algorithms.
Bring your own ant colony optimization algorithm
You can see that including your own algorithm in this
application is simple.
- First, write your algorithm class derived from
CASTravelBase. Append
files TravelAlg.h and TravelAlg.cpp to do that. It will save you
from headaches of finding and including the appropriate headers if you would use
separate algorithm files. - If your algorithm has parameters, declare them as static data
members of your class. Provide a dialog box or another means to set these
parameters. Remember that you have to provide a pair of static date
members, the value, and the value name string for each parameter to ensure
saving/loading the parameters to/from XML files by the application.
- Add your class type to the
TypeList definition of AlgTypeList. Do not forget
to change the number in the TypeList macro; for
example, if you are adding a class, change TYPELIST_6 to TYPELIST_7, etc. - Compile, build, and run.
Bring your own statistics
It is similar, but more complicated. In addition to your own
statistics class and the correction of the statistics type list you will have to
add a button to the statistics selection dialog box, and your charts (if any)
to the function CAntColDlg::ResetStChartData
in AntColDlg.cpp.
Running an algorithm
Select an algorithm, its parameters, and the appropriate
statistics. After selection, the algorithm and its parameters and the selected
statistics are committed by clicking on the button Apply (function CAntColDlg::OnBnClickedBtnapply()). It enables the buttons
Run or Step. Clicking on one of these buttons will start a worker thread. The thread receives
the function:
unsigned _stdcall CAntColDlg::RunASTravel(void* colDataPtr)
with the pointer to CAntColDlg as a parameter:
m_hWorkThread = (HANDLE)_beginthreadex(NULL, 0, CAntColDlg::RunASTravel, this, CREATE_SUSPENDED , NULL);
The execution of the algorithm is controlled by this function and the function:
CAntColDlg::OnTravelOnce(WPARAM wParam, LPARAM lParam)
In C++ 11 there is a new class std::thread that accepts worker functions with many
parameters. I did not use it because this class is included in VS 2012 only.
Here is the pseudo code for the worker function CAntColDlg::RunASTravel:
- Prepare an array of event
objects to synchronize the worker and the main threads
- Get the max trials
number and enter the loop to execute the trips
- Reset the ant colony
- Travel the colony
graph for all colony's ants for the selected algorithm
- Upon the end of each
trip analyze the requests for graph snapshots and set the snapshot flag if the
snapshot trigger is signaled
- Calculate and save
statistics for the trip
- Check for reset and
mutation conditions and do reset or mutation if needed
- Update the ant colony
graph pheromones
- Check whether it is time to send data to the main thread for periodic display of the travel state
(every 100 trips) or to allow a snapshot to be taken and set the appropriate
control events
- Enter the wait
function and wait on events
- Exit the wait function
if appropriate and return to the beginning of the trip loop
Let us discuss the synchronization of the worker and main
threads.
Synchronization of the worker and the main threads
We are using four Windows event
objects to synchronize the worker and main threads.
The event handles are members of CAntColDlg and are created in CAntColDlg::OnInitDialog:
m_hEvAbortRun = CreateEvent(NULL, FALSE, FALSE, NULL);m_hEvStopReq = CreateEvent(NULL, FALSE, FALSE, NULL);m_hEvInfoReq = CreateEvent(NULL, FALSE, FALSE, NULL);m_hEvContRun = CreateEvent(NULL, TRUE, TRUE, NULL);
The events are ordered at the start of the worker thread in two arrays:
HANDLE syncEvArr[] =
{
antColDlgPtr->m_hEvAbortRun, antColDlgPtr->m_hEvStopReq,
antColDlgPtr->m_hEvInfoReq, antColDlgPtr->m_hEvContRun
};
HANDLE waitEvArr[] =
{
antColDlgPtr->m_hEvAbortRun,
antColDlgPtr-m_hEvContRun
};
The events are initialized:
ResetEvent(syncEvArr[0]);
ResetEvent(syncEvArr[1]);
ResetEvent(syncEvArr[2]);
SetEvent(syncEvArr[3]);
The event to continue the run
is last in both arrays. At the start, only the event to continue run is signaled.
After the worker thread
finishes processing of the trip, it enters the wait function:
DWORD dwWait = WaitForMultipleObjects(4, syncEvArr, FALSE, INFINITE);
switch (dwWait)
{
case WAIT_OBJECT_0: antColDlgPtr->PostMessage(UWM_ONCETRAVELED, MODE_FAIL, runCnt);
return MODE_FAIL;;
case WAIT_OBJECT_0 + 1: if (antColDlgPtr->m_citiesMode == MODE_STEP)
antColDlgPtr->PostMessage(UWM_ONCETRAVELED, MODE_STEP, runCnt);
else
antColDlgPtr->PostMessage(UWM_ONCETRAVELED, MODE_STOP, runCnt);
dwWait = WaitForMultipleObjects(2, waitEvArr, FALSE, INFINITE);
switch (dwWait)
{
case WAIT_OBJECT_0: antColDlgPtr->PostMessage(UWM_ONCETRAVELED, MODE_FAIL, runCnt);
return MODE_FAIL;
case WAIT_OBJECT_0 + 1: break;
}
break;
case WAIT_OBJECT_0 + 2: antColDlgPtr->PostMessage(UWM_ONCETRAVELED, MODE_RUN, runCnt);
dwWait = WaitForMultipleObjects(2, waitEvArr, FALSE, INFINITE);
switch (dwWait)
{
case WAIT_OBJECT_0: antColDlgPtr->PostMessage(UWM_ONCETRAVELED, MODE_FAIL, runCnt);
return MODE_FAIL;
case WAIT_OBJECT_0 + 1: break;
}
break;
case WAIT_OBJECT_0 + 3: break;
}
If the main thread (the user) wants to stop or interrupt test
execution, it should reset the continue event and set one of the
other events, like this:
if (m_citiesMode == MODE_RUN)
{
ResetEvent(m_hEvContRun);
SetEvent(m_hEvInfoReq);
}
The first action is to reset m_hEvContRun. Because all other events are normally
non-signaled, the worker thread will go into the wait state. It waits until the
user will set any other event to the signaled state. That will release the
worker thread, and the worker function will go to the switch statement to
process the return from the first wait function.
First, the worker thread posts a message to the main thread:
antColDlgPtr->PostMessage(UWM_ONCETRAVELED, MODE_RUN, runCnt);
The worker thread passes the appropriate values to WPARAM and LPARAM of the message.
If the user requested an interruption of the test (had set event m_hEvStopReq or m_hEvInfoReq),
to initiate one step or stop
of execution, or the application requested the information on the state
of the travel, the worker thread enters the second wait functions, to
wait for the
user choice to continue or to abort the run. This time the worker thread
is waiting for two events only.
The messages the worker thread sends to the main thread are
handled in the function CAntColDlg::OnTravelOnce(WPARAM wParam, LPARAM lParam) (file AntColDlg.cpp).
This function, after completing all processing, sets the
event m_hEvContRun if the user wants to continue the run. That releases the
worker thread if it was waiting.
After completing the run, the worker thread sends to the main
thread the message:
antColDlgPtr->PostMessage(UWM_ONCETRAVELED, MODE_APPLY, runCnt);
and exits.
Drawing with GDI+
All drawing is rendered in GDI+. To get flicker free
rendering, I am drawing onto a memory bitmap and only at the end of the drawing transfer the bitmap
onto the screen surface (this is well known as double buffering). Here is an
example:
void CStCities::OnPaint()
{
CPaintDC dc(this); Graphics gr(dc.m_hDC); Rect rGdi;
gr.GetVisibleClipBounds(&rGdi); rGdi.Width -= 1; rGdi.Height -= 1; Bitmap clBmp(rGdi.Width, rGdi.Height); Graphics* grPtr = Graphics::FromImage(&clBmp); .................................................
.................................................
gr.DrawImage(&clBmp, rGdi);
delete grPtr;
}
Second, to display the start cities as a bar graph, I used a transparent
picture control CCitiesChart.
I overlapped it over the main dialog chart control. The code
is in CAntColDlg::OnInitDialog():
WINDOWPLACEMENT contPlacement;
m_chartContainer.GetWindowPlacement(&contPlacement);
m_stCitiesChart.SetWindowPlacement(&contPlacement);
Printing outside a document/view model
In the
article KB133275, Microsoft
explains how to print from a class other than an MFC CView. In addition,
there is a tutorial on GDI Printing,
GDI+ Printing on Internet. The tutorial is overcomplicated; Microsoft does
not mention GDI+.
Still,
I followed the framework of the Microsoft sample code.
For
example, this is how I am printing a report of the results of the test.
First,
you start with CPrintDialog to select the printer and get the printer DC (AntColDlg.cpp):
void CAntColDlg::PrintReport(void)
{
CPrintDialog printDlg(FALSE,PD_USEDEVMODECOPIES|PD_HIDEPRINTTOFILE|PD_NOPAGENUMS|
PD_NOSELECTION|PD_RETURNDC);
printDlg.m_pd.Flags &= ~PD_SHOWHELP;
printDlg.m_pd.Flags &= ~PD_NOSELECTION;
if (IDOK == printDlg.DoModal())
{
CPaintDC containerDC(this);
int scrDpiX = containerDC.GetDeviceCaps(LOGPIXELSX);
CPrnReport prnReport; prnReport.InitRepData(this);
bool bPrintSel = printDlg.PrintSelection() == TRUE ? true : false;
prnReport.PrintReport(scrDpiX, bPrintSel, printDlg.GetPrinterDC());
}
}
All work is done in the function (file PrnReport.cpp):
void CPrnReport::PrintReport(int scrDpiX, bool bPrintSel, HDC printDC)
{
if (printDC != NULL)
{
CDC* pDC = new CDC;
pDC->Attach(printDC);
Graphics* grPtr = Graphics::FromHDC(printDC); grPtr->SetPageUnit(UnitDocument);
grPtr->SetSmoothingMode(SmoothingModeAntiAlias);
float dpiRatioX = 300.0f/scrDpiX;
RectF rGdiF;
grPtr->GetVisibleClipBounds(&rGdiF); pDC->StartDoc(m_algName.c_str()); pDC->StartPage();
.......................................... pDC->EndPage();
if (!bPrintSel)
{
...........................................
while (true)
{
pDC->StartPage();
................................. pDC->EndPage();
if (firstRow == rowsTotal)
break;
}
}
pDC->EndDoc();
delete(pDC);
}
}
Pay attention to the use of MFC functions StartDoc, StartPage,
EndPage, and EndDoc.
Creating a custom print dialog
The recipe is known: find the
CPrintDialog resource template in MFC, copy it, extend it, and write your own
class derived from CPrintDialog with all the bells and whistles you like.
I spent a lot of time trying to
find the appropriate resource, and I have found it eventually. You can copy
IDD_DLGEDGEPRINT from this application to save some time.
You have to initialize the
members of the m_pd structure of CFileDialog
like this (file DlgEdgePrint.cpp):
CDlgEdgePrint::
CDlgEdgePrint(BOOL bPrintSetupOnly, DWORD dwFlags, CWnd* pParentWnd)
: CPrintDialog(bPrintSetupOnly, dwFlags, pParentWnd)
{
m_pd.lpPrintTemplateName = (LPTSTR) MAKEINTRESOURCE(IDD_DLGEDGEPRINT);
m_pd.Flags |= PD_ENABLEPRINTTEMPLATE;
m_pd.Flags &= ~PD_SHOWHELP;
m_pd.hInstance = AfxGetInstanceHandle();
}
You also have to write handlers for controls you added to the dialog template.
In my custom print dialog, I have added only a CStatic control to display a warning that was known before the print dialog
was instantiated:
sstream_t stream_t;
stream_t << _T("Selected screen page takes ") << paperPagesPerScrPage
<< _T(" paper pages,\n") << _T("All pages need ")
<< totalPaperPages << _T(" paper pages.\n")
<< _T("Screen page #1 shows ant's path,\nfor other pages")
<< _T(" source vertex's ID = page nmb -2") << endl;
string_t str = stream_t.str();
const _TCHAR* buf = str.data();
I have initialized the m_pd members as follows:
CDlgEdgePrint printDlg(FALSE, PD_SELECTION|PD_USEDEVMODECOPIES|PD_HIDEPRINTTOFILE||PD_RETURNDC);
printDlg.m_pd.Flags &= ~PD_SHOWHELP;
printDlg.m_pd.Flags |= PD_ENABLEPRINTHOOK;
printDlg.m_pd.lpfnPrintHook = PrintHookProc;
printDlg.m_pd.nFromPage = WORD(selPage + 2);
printDlg.m_pd.nToPage = WORD(selPage + 2);
printDlg.m_pd.nMinPage = 1;
printDlg.m_pd.nMaxPage = WORD(pagesNum);
printDlg.m_pd.lCustData = (LPARAM)buf;
I wrote this text in the static control on initialization of the dialog calling the callback function PrintHookProc:
UINT_PTR CALLBACK PrintHookProc(HWND hdlg, UINT uiMsg, WPARAM wParam, LPARAM lParam)
{
UNREFERENCED_PARAMETER(wParam);
switch(uiMsg)
{
case WM_INITDIALOG:
{
PRINTDLG* pd = (PRINTDLG*)lParam;
const _TCHAR* buf = (_TCHAR*)pd->lCustData;
HWND tbHWND = (HWND)GetDlgItem(hdlg, IDC_EDGEPRN_STWARN);
SetWindowText(tbHWND, buf);
} break;
}
return FALSE;
}
The source code and demo project
With this article, I have
included the application source code and the AntCol.exe file.
With the source code are
included the libraries it uses: ChartCtrlLibD.lib (Debug version 1.2.1) and
ChartCtrlLib.lib (Release version 1.2.1.) You will be able to recompile and
rebuild AntCol.exe with your own algorithms.
The code was built under MS
Visual Studio 2012 (VC++ 11) and Windows & Pro.
If you do not have VS
2012, you still can work with the source code in MS VS 2010. I included the
solution and project files in the folder 2010Project in the source zip file.
The source files are the same, the only difference is that for VC++ 11, the
project properties include a preprocessor directive _VARIADIC_MAX=10, because
in VC++ 11 Microsoft uses variadic templates for templates with many arguments,
and default max number of elements is five. In VC++ 10, they are using
recurrent definitions like we used for TypeList.
To work in VS 2010, you will
need VC++ 10 versions of the static library ChartCtrlLib.lib. You can download
them from my article: An
MFC Chart Control with Enhanced User
Interface.
History
- 08/22/2013: Initial version,
1.0.0.
