Introduction
Writing an expression evaluation module is a basic skill for a programmer like my teacher says, and yes it is, when you want to write a module to evaluate a mathematics expression, you should know well some kinds of data structure, algorithm, and the advanced features of the language that you use. Recently I reworked a biochemical system analysis core module in
Visual Basic of the program PLAS which was written by Antonio E.N.Fereira (and I will share this work in my next article on
CodeProject), and in this analysis module I needed a module to evaluate a set of equations, so I wrote a mathematics evaluation module. And at here I will share my work of this mathematics evaluation module.
Using the code
A mathematic expression may have functions, constants, specific operators, and a
very important thing: the bracket expression! Here is a complex example:
Max(Log((((sin(tan(20)^5+50)*40)!-(99*Rnd(4,20)))%((56+8*cos(PI))^2)^-2.3)!^4), log(e))^3
The expression that I have shown above is the most complicated expression that I think will appear in my rework. This expression is in accordance with the syntax of the mathematics expression in the language
Visual Basic (except the operators % and !). In my opinion, a mathematics expression can be classified as
one of two types: a simple expression with only numbers and operators in it, or a complex expression with functions, operators, and bracket pairs. And the complex expression consists
of several simple expressions and functions.
SimpleExpression
1. The basic arithmetic calculation
Here are the arithmetic operators in a simple expression:
+(Plus), -(Subtraction), *(Multiplication), /(Division), \(Exact Division), ^(Power), %(Mod), !(Factorial)
And I use an array of delegates (or Lambda expressions) to carry out these operations:
Public Shared ReadOnly Arithmetic As System.Func(Of Double, Double, Double)() = {
Function(a As Double, b As Double) a + b,
Function(a As Double, b As Double) a - b,
Function(a As Double, b As Double) a * b,
Function(a As Double, b As Double) a / b,
Function(a As Double, b As Double) a \ b,
Function(a As Double, b As Double) a Mod b,
Function(a As Double, b As Double) System.Math.Pow(a, b),
AddressOf Factorial}
Because Visual Basic has no operators for factorial calculation, I have to write a function to do factorial calculation of a number.
Here is the factorial calculation function:
Public Shared Function Factorial(a As Double, b As Double) As Double
If a <= 0 Then
Return 1
Else
Dim n As Integer = a
For i As Integer = n - 1 To 1 Step -1
n *= i
Next
Return n
End If
End Function
Because I don’t know how to do factorial calculation of a negative number, I make the result of a negative number in this function return number ‘’1’.
As you can see in the Delegate array definition: Function(....) is equal to the declared form of
the AddressOf keyword. In fact a delegate Lambda in
Visual Basic can be declared in these three ways:
(a) simplest only in one line:
Function(<paramenter list>) <only one line statement>
(b) much complicated way in sevral lines with no function name:
Function(<paramenter list>) As <Result type>
<Statements>
End Function
(c) declare as a normal function but should use AddressOf keyword to get this
function(AddressOf is just like a operator to get the pointer of a function)
AddressOf <function name>
And the most important thing is that the function should have the same signature
as the delegate that you declare (the same signature means the same parameters and the same return type no matter
if the name is the same or not).
I have defined these basic arithmetic operations as a helper class and you can find this helper class in the namespace of
Helpers in my uploaded project. This helper class has an interface that uses these arithmetic operators:
Public Shared Function Evaluate(a As Double, b As Double, o As Char) As Double
Dim idx As Integer = InStr(OPERATORS, o) - 1
Return Arithmetic(idx)(a, b)
End Function
So, in this interface function, the operator delegate was indexing from the operator character that we parsed from the expression using a constant string:
Public Const OPERATORS As String = "+-*/\%^!"
2. The meta expression
As you can see, a simple expression has only numbers and operators, so in my
personal view a simple expression can be divided into many meta expressions. Here is how
I define a meta expression: a meta expression is an expression token with only an operator and a number on the left side of this operator. So we can get the data structure of the meta expression as:
Public Class MetaExpression
<Xml.Serialization.XmlAttribute> Public [Operator] As Char
<Xml.Serialization.XmlAttribute> Public LEFT As Double
Public Overrides Function ToString() As String
Return String.Format("{0} {1}", LEFT, [Operator])
End Function
End Class
Then we can treat a simple expression as an ordered list of these meta expressions:
Public Class SimpleExpression
Friend MetaList As New List(Of MetaExpression)
And the function below is a simple function to restore this meta expression list to an expression
of string type:
Public Overrides Function ToString() As String
Dim s As StringBuilder = New StringBuilder(128)
For Each e In MetaList
s.Append(e.ToString)
Next
Return s.ToString
End Function
How do we parse the simple expression into a meta expression list? I do the parsing work in the
Construct method of the simple expression class:
Public Shared Widening Operator CType(expression As String) As SimpleExpression
Using the CType construct method will make your code more
natural to a human language like:
Dim Result As SimpleExpression = "(1+1)*2"
I’m also making an output conversion method:
Shared Narrowing Operator CType(e As SimpleExpression) As Double
This CType construct method will also make your code more
natural like:
Dim Result2 As Double = Result
So how do I do my meta expression parsing job? At first I use a regular
expression to parse all of the real numbers that appear in the simple expression:
Dim Numbers As MatchCollection = Regex.Matches(ClearOverlapOperator(expression), DOUBLE_NUMBER_REGX)
And a real number is a Double type number in Visual Basic, it looks like the pattern shown below:
Public Const DOUBLE_NUMBER_REGX As String = "-?\d+([.]\d+)?"
Using a regular expression makes our job a little slow, but this can be
solved by upgrading the CPU in our computer, and in fact this method is what we usually do in our lab,
err........ never mind.
We assume that the previous and the next token of each number is an operator,
so that we can parse the simple expression into a list of meta expressions following these steps:
(1) Get the string value of a number from the MatchCollection
(2) Get the String length of this number and then we can get the reading position in the
simple expression and then we can using the string length to skip the current read number
and the next character in the expression will be a operator
(3) Using current number and the operator that appears next to
the current number then we can generate a meta expression
So here is how it works:
Dim s As String = Numbers(0).Value
Dim p As Integer = Len(s)
Dim o As Char = expression.Chars(p)
NewExpression.MetaList.Add(New MetaExpression With {.LEFT = Val(s), .Operator = o})
p += 1
For i As Integer = 1 To Last - 1
s = Numbers(i).Value
If NewExpression.MetaList.Last.Operator = "-"c Then
p += Len(s) - 1
s = Mid(s, 2)
Else
If expression.Chars(p) = "+"c Then
p += Len(s) + 1
Else
p += Len(s)
End If
End If
o = expression.Chars(p)
p += 1
NewExpression.MetaList.Add(New MetaExpression With {.LEFT = Val(s), .Operator = o})
Next
Finally we get a meta expression list: NewExpression, this is our simple expression object.
3. Calculate the simple expression
The simpleExpression has a function to calculate its value:
Public Function Evaluate() As Double
We write a calculator function that can do a specific set of operators calculation, and this feature makes the operator work easily like:
Calculator("^")
Calculator("*/\%")
Calculator("+-")
Return MetaList.First.LEFT
In the function of Calculator, it accepts the operator list that will do the calculation, and then operates the module variable
MetaList. When done with an operator, it will remove an element in the list, so that finally the metalist only contains one element, and this element is the calculation result.
Friend Sub Calculator(OperatorList As String)
Dim LQuery As Generic.IEnumerable(Of MetaExpression) =
From e As MetaExpression In MetaList
Where InStr(OperatorList, e.Operator) > 0
Select e
Dim Counts As Integer = LQuery.Count
Dim M, NextElement As MetaExpression
For index As Integer = 0 To MetaList.Count - 1
If Counts = 0 OrElse MetaList.Count = 1 Then
Return
ElseIf OperatorList.IndexOf(MetaList(index).Operator) <> -1 Then
M = MetaList(index)
NextElement = MetaList(index + 1)
NextElement.LEFT = Arithmetic.Evaluate(M.LEFT, NextElement.LEFT, M.Operator)
MetaList.RemoveAt(index)
index -= 1
Counts -= 1
End If
Next
End Sub
4. Testing
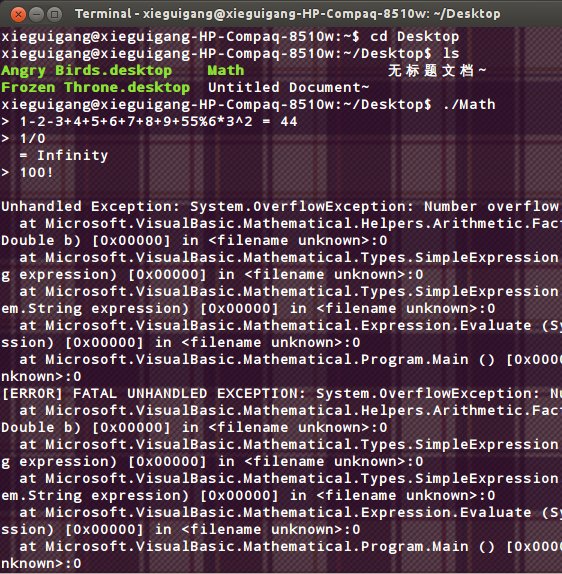
Dim sExpression As String = "1-2-3+4+5+6+7+8+9+55%6*3^2"
Dim e As Microsoft.VisualBasic.Mathematical.Types.SimpleExpression = sExpression
Console.WriteLine("> {0} = {1}", sExpression, e.Evaluate)
Console output:
> 1-2-3+4+5+6+7+8+9+55%6*3^2 = 44
ComplexExpression
An expression that has only basic operators is not enough for our biochemical system analysis work, so we must get a more complex class to deal with the function and the bracket pairs situation that occurs in our research. But at first I should introduce the function calculation work:
1. The function calculation engine
In this helper class, we list all of the math functions available in Visual Basic, and as
with the basic arithmetic operators delegates in the previous section, the
function calculation engine should also consist of a delegate array, but as we
should use a name to identify each function, we use a Dictionary object to store this array:
Public Shared ReadOnly Functions As Dictionary(Of String, System.Func(Of Double, Double, Double)) =
New Dictionary(Of String, System.Func(Of Double, Double, Double)) From {
{"abs", Function(a As Double, b As Double) Math.Abs(a)},
{"acos", Function(a As Double, b As Double) Math.Acos(a)},
{"asin", Function(a As Double, b As Double) Math.Asin(a)},
{"atan", Function(a As Double, b As Double) Math.Atan(a)},
{"atan2", Function(a As Double, b As Double) Math.Atan2(a, b)},
{"bigmul", Function(a As Double, b As Double) Math.BigMul(a, b)},
{"ceiling", Function(a As Double, b As Double) Math.Ceiling(a)},
{"cos", Function(a As Double, b As Double) Math.Cos(a)},
{"cosh", Function(a As Double, b As Double) Math.Cosh(a)},
{"exp", Function(a As Double, b As Double) Math.Exp(a)},
{"floor", Function(a As Double, b As Double) Math.Floor(a)},
{"ieeeremainder", Function(a As Double, b As Double) Math.IEEERemainder(a, b)},
{"log", Function(a As Double, b As Double) Math.Log(a)},
{"log10", Function(a As Double, b As Double) Math.Log10(a)},
{"max", Function(a As Double, b As Double) Math.Max(a, b)},
{"min", Function(a As Double, b As Double) Math.Min(a, b)},
{"pow", Function(a As Double, b As Double) Math.Pow(a, b)},
{"round", Function(a As Double, b As Double) Math.Round(a)},
{"sign", Function(a As Double, b As Double) Math.Sign(a)},
{"sin", Function(a As Double, b As Double) Math.Sin(a)},
{"sinh", Function(a As Double, b As Double) Math.Sinh(a)},
{"sqrt", Function(a As Double, b As Double) Math.Sqrt(a)},
{"tan", Function(a As Double, b As Double) Math.Tan(a)},
{"tanh", Function(a As Double, b As Double) Math.Tanh(a)},
{"truncate", Function(a As Double, b As Double) Math.Truncate(a)},
{"rnd", AddressOf Microsoft.VisualBasic.Mathematical.Helpers.Function.RND},
{"int", Function(a As Double, b As Double) CType(a, Integer)},
{String.Empty, Function(a As Double, b As Double) a}}
2. Parsing the expression
It is not easy to parse an expression with functions and bracket pairs in it, but it still can be solved although this coding job may make the programmer angry.
The function Evaluate is the entry to this parsing job, it accepts a string expression and then parses it into
a simple expression then calculates the simple expression:
Public Shared Function Evaluate(expression As String) As Double
How do we parse the bracket pair? We assume that only one kind of bracket
pair is allowed in the expression as Visual Basic only allows the bracket pair () appear in its math expressions, so we only need a stack to record the positions of the left bracket:
Dim LBStack As New Stack(Of Integer)
We use a variable p to point to the position that we read on the expression string, and when the value of
p is equal to the position of the last char in the expression, it means we have done our calculation work. So we can use this condition
in the While loop:
Do While p <= Expression2.Length - 1
Loop
The program reads the string from the left side to the right side char by char. When it reads a char of
the left side bracket, it pushes the position p to the stack and then goes on reading for a right side bracket. When it reads a right side bracket it looks for the last left side bracket in the stack, if the stack is empty, that means a syntax error in the expression, and when the stack is not empty, then we get a simple expression.
At last using the Mid function we get this simple expression and then evaluate it into a number.
This work seems easy, but the fact is this work is much more complicated than we could think: First, the function gets a bracket pair so some bracket pairs
are not independent. Next, some functions get two parameters, so a comma character may exist in the expression.
So we treat the bracket pair character and the comma as a flag character in our parsing job:
If Expression2.Chars(p) = "("c Then
ElseIf Expression2.Chars(p) = ")"c Then
ElseIf Expression2.Chars(p) = ","c Then
End If
As previously described: when we read a left side bracket pair char, we push the current reading position to the stack and then read
the next character:
LBStack.Push(item:=p + 1)
And then the horrible thing comes: we must parse the function in our expression. As a complex expression may exist as one of the parameters of the function, this situation makes our coding job not so happy. But after observing the pattern of the expression, we find out that a pattern exists in the expression likes: Function(<Expression>) or Function(<Expression1>, <Expression2>), the expression in the
parameter of the function, maybe another function expression, we can do this evaluation recursion: use the function
Evaluate(expression As String) As Double again to get the value of this
parameter expression.
So the code finally looks like this:
Do While p <= Expression2.Length - 1
If Expression2.Chars(p) = "("c Then
LBStack.Push(item:=p + 1)
ElseIf Expression2.Chars(p) = ")"c Then
LBLocation = LBStack.Pop
se = Mid(Expression2.ToString, LBLocation + 1, p - LBLocation)
r = se
LBLocation += 1
If LBLocation < Expression2.Length AndAlso OPERATORS.IndexOf(Expression2.Chars(LBLocation)) = -1 Then
Dim f = GetFunctionName(Expression2, LBLocation)
Call CalcFunction(f, r.Evaluate, 0, 1)
Else
Expression2.Replace("(" & se & ")", r.Evaluate)
p -= Len(se)
End If
ElseIf Expression2.Chars(p) = ","c Then
LBLocation = LBStack.Peek
se = Mid(Expression2.ToString, LBLocation + 1, p - LBLocation)
a = CType(se, Types.SimpleExpression)
LBStack.Push(item:=p + 1)
p += 1
Dim LBStack2 As New Stack(Of Integer)
Do While p <= Expression2.Length - 1
If Expression2.Chars(p) = "("c Then
LBStack2.Push(item:=p + 1)
ElseIf Expression2.Chars(p) = ")"c Then
If LBStack2.Count = 0 Then Exit Do Else LBStack2.Pop()
End If
p += 1
Loop
LBLocation = LBStack.Pop
se = Mid(Expression2.ToString, LBLocation + 1, p - LBLocation)
b = Evaluate(se)
LBLocation = LBStack.Pop
Dim f = GetFunctionName(Expression2, LBLocation)
Call CalcFunction(f, a, b, 0)
End If
p += 1
Loop
Finally, we calculate all of the expressions in the bracket pairs and the function, and at last we get a simple expression, and then we calculate
this expression using the SimpleExpression class object and get the final result of this expression. Here is the whole code of this function:
Public Shared Function Evaluate(expression As String) As Double
Dim LBStack As New Stack(Of Integer)
Dim r As Microsoft.VisualBasic.Mathematical.Types.SimpleExpression, se As String
Dim LBLocation As Integer
Dim Expression2 As StringBuilder = New StringBuilder(value:=expression)
Dim a, b As Double
Dim p As Integer, CalcFunction As System.Action(Of String, Double, _
Double, Integer) = Sub(Func As String, pa As Double, pb As Double, d As Integer)
pa = Microsoft.VisualBasic.Mathematical.Helpers.Function.Functions(Func)(pa, pb)
LBLocation -= Len(Func) + d
se = Mid(Expression2.ToString, LBLocation, p - LBLocation + 2)
Expression2.Replace(se, pa)
p -= Len(se)
End Sub
Do While p <= Expression2.Length - 1
If Expression2.Chars(p) = "("c Then
LBStack.Push(item:=p + 1)
ElseIf Expression2.Chars(p) = ")"c Then
LBLocation = LBStack.Pop
se = Mid(Expression2.ToString, LBLocation + 1, p - LBLocation)
r = se
LBLocation += 1
If LBLocation < Expression2.Length AndAlso _
OPERATORS.IndexOf(Expression2.Chars(LBLocation)) = -1 Then
Dim f = GetFunctionName(Expression2, LBLocation)
Call CalcFunction(f, r.Evaluate, 0, 1)
Else
Expression2.Replace("(" & se & ")", r.Evaluate)
p -= Len(se)
End If
ElseIf Expression2.Chars(p) = ","c Then
LBLocation = LBStack.Peek
se = Mid(Expression2.ToString, LBLocation + 1, p - LBLocation)
a = CType(se, Types.SimpleExpression)
LBStack.Push(item:=p + 1)
p += 1
Dim LBStack2 As New Stack(Of Integer)
Do While p <= Expression2.Length - 1
If Expression2.Chars(p) = "("c Then
LBStack2.Push(item:=p + 1)
ElseIf Expression2.Chars(p) = ")"c Then
If LBStack2.Count = 0 Then Exit Do Else LBStack2.Pop()
End If
p += 1
Loop
LBLocation = LBStack.Pop
se = Mid(Expression2.ToString, LBLocation + 1, p - LBLocation)
b = Evaluate(se)
LBLocation = LBStack.Pop
Dim f = GetFunctionName(Expression2, LBLocation)
Call CalcFunction(f, a, b, 0)
End If
p += 1
Loop
Return CType(Expression2.ToString, Microsoft.VisualBasic.Mathematical.Types.SimpleExpression)
End Function
3. Testing
Module Program
Function Main() As Integer
Dim Cmd As String = String.Empty
#If DEBUG Then
Dim sExpression As String = "1-2-3+4+5+6+7+8+9+55%6*3^2"
Dim e As Microsoft.VisualBasic.Mathematical.Types.SimpleExpression = sExpression
Console.WriteLine("> {0} = {1}", sExpression, e.Evaluate)
#End If
Console.Write("> ")
Do While Cmd <> ".quit"
Cmd = Console.ReadLine
Console.WriteLine(" = {0}", Expression.Evaluate(Cmd))
Console.Write("> ")
Loop
Return 0
End Function
End Module
A tiny mathematical script engine
How to parse a constant
A constant is a fake variable that its value will not change at any time. When we want to parse a constant from the expression, we should get the constant name first. And then we could parse the constant from the expression, but the problem is that a constant name maybe too short that it may appear in the function name or a variable name, like:
pie+pi+e
Where pie is a variable name and then pi and e
are constant names. When we replace the constant name with a value directly, it
would disrupt the variable pie,
and that is terrible. So the constant parsing job goes horrible.
From observing the pattern of the constant, we find that the pattern of a constant is:
[Operator][Constant Name][Operator]
And this pattern is as well as the variable or a number does too. So from this point we could make the constant and variables’ name parsing job. Here is how we do
it:
- Get a name list, and this list is ordered by the string length in descending
order.
- Use the
InStr function to get the position of this constant name in the expression. - This step is the key step: get the previous char and the next token char of the position that we get, and then
see if both of them are operators or not.
- If true, then we get a constant, and replace this token with the constant value.
- If not, then get the next position of the constant with the overloaded function of
InStr. - Next loop.
So, let’s see how my code works in the function Function Replace(expression As String) As String:
At first, in case of the constant appearing at the beginning and the last position of the expression, we make the expression add zero to make this horrible situation easy:
expression = "0+" & expression & "+0"
and then a For loop to replace all of the constants in the module:
For Each [Const] In ConstantList
Dim p As Integer = InStr(expression, [Const]), _
l As Integer = Len([Const])
c = Constants([Const])
Variable p is the position of the specific constant in our expression, so using
the function we get a position, this position maybe the position of the constant or just partly variable or function name.
Next we get the character between this constant, and see of it is a constant name or not:
Do While p
Right = expression(p + l - 1)
Left = expression(p - 2)
If InStr(LEFT_OPERATOR_TOKENS, Left) AndAlso InStr(RIGHT_OPERATOR_TOKENS, Right) Then
s = Mid(expression, p - 1, l + 2)
Call sBuilder.Replace(s, Left & c & Right)
expression = sBuilder.ToString
p = InStr(p + Len(c), expression, [Const])
Else
p = InStr(p + l, expression, [Const])
End If
Loop
If we get a constant, then we replace it with its value; if not, we go to the next position:
p = InStr(p + l, expression, [Const])
The user variables parsing is the same as the constant parsing, and the difference between the constant and the variables is that the constant is stored in a dictionary so that we can not modify its value again after we create it, and the variable is stored in a hashtable so that we
can modify its value in the feature.
Please notice that we do the constant parsing job before we do the variable parsing job in the function
Expression.Evaluate:
expression = Helpers.Constants.Replace(expression)
expression = Helpers.Variable.Replace(expression)
so that the constant has higher privilege than the variable, that means if we get a constant named o and a variable which has the same name, the constant will override the value of the variable o.
Write a simple script engine for mathematics calculation
Here I write a simple script execution engine for my mathematics evaluator, it
has only three commands so far, take a look at how it works:

How this engine works
Commands are stored in a dictionary in the form of {Name, Action}:
Friend Shared ReadOnly StatementEngine As Dictionary(Of String, System.Action(Of String)) =
New Dictionary(Of String, System.Action(Of String)) From {
{"const", AddressOf Helpers.Constants.Add},
{"function", AddressOf Helpers.Function.Add},
{"var", AddressOf Helpers.Variable.Set},
{".quit", Sub(NULL As String) NULL = Nothing}}
Each command has a parameter of Statement As String, and the
entry function Function Shell(statement As String) As String. We split the string that
the user inputs from the console to get the command name. Please notice that, in the statement syntax of my tiny script engine, the command name always appears at the first place of the statement. Here is the syntax and the usage information of the
three commands and an additional value assignment command:
Name
| Syntax
| Information
| Example
|
const
| const <const_name> value
| Declare a new constant
| Const p 123
|
function
| function <function_name> expression
| Declare a new function
| Function f log(x^3+e)-y
|
var
| var <var_name> value
| Declare a new variable or assign the value to the variable
| Var p2 0.123
|
Value assignment
| <var_name> <- expression
| Assign the value of the expression to the variable
| P2 <- f(pi!,pow(e,5))
|
Declare a const or variable
The constant is the same as the variable, but we could not change the value of the constant again, here is how we declare a new constant or a variable:
Public Shared Sub Add(Name As String, value As String)
Constants.Add(Name.ToLower, value)
ConstantList.Clear()
Dim Query As Generic.IEnumerable(Of String) = From s As String In Constants.Keys
Select s
Order By Len(s) Descending
Call ConstantList.AddRange(Query.ToArray)
End Sub
At first we add the new constant to the constant dictionary, and then regenerate the constant name list for the replacement of the constant value in the future calculation.
The variable declaration does the same thing.
Declare a function
Declare a function same as the constant and variable, and it has only two
parameters to replace because the math function Visual Basic has a maximum of
only two parameters. So we first replace the function parameter x and y
with a long string that could hardly be the same as that the user declared of any object in my script engine, and then, when we calculate a user function, we can replace this string directly
with its value. At last we use the shared function of Expression.Evaluate to get the value of this user function using a delegate function.
Public Shared Sub Add(Name As String, Expression As String)
Dim [Function] As System.Func(Of Double, Double, Double)
Expression = Constants.Replace(Expression)
Expression = Replace(Expression)
[Function] = Function(DblX As Double, DblY As Double) As Double
Dim sBuilder As StringBuilder = New StringBuilder(Expression)
sBuilder.Replace(X, DblX)
sBuilder.Replace(Y, DblY)
Return Microsoft.VisualBasic.Mathematical.Expression.Evaluate(sBuilder.ToString)
End Function
Call Add(Name.ToLower, [Function])
End Sub
Variable value assignment
Variable <- expression
The expression could be any mathematics expression with the syntax of a
mathematics expression in Visual Basic. And actually the value assignment statement in my script engine is another way of variable declaration:
> var x1 123
> x1
= 123
> x2 <- 33
> x2
= 33
>
A special variable
Variable $ is a system reserved variable to keep the calculation value of the last expression.
> $ <- e
> $
= 2.71828182845905
> sin(e)
= 0.410781290502904
> $
= 0.410781290502904
>
I makes the character $ a system reserved variable because I am going to add the feature of multiple line script file calculation in my script engine just like
the m file in Matlab. And this system reserved variable will keep the calculation result of each script file and return it to the script engine
to assign the value to the parent function which will call the script file or the script text.
This program was developed on Microsoft Visual Studio 2013 Preview, Microsoft Windows 7 Ultimate, and successfully debugged and tested
on Ubuntu 13.04 (Mono 2.1).
