A C++ Karnaugh Map Minimizer (Infinite Variables)

• Download source code   
• Download executable file 

Introduction

This code provides a C++ program that implements a Karnaugh map (k-map) minimizer with an algorithm that can get a solution for all k-map's types, i.e., for k-maps with any number of variables, but it has been implemented in this program for 26 variables only as much as the number of letters in the English alphabet.  

Background  

The reader should have the basics of Boolean algebra and k-map usage in order to get the most benefit from this article.

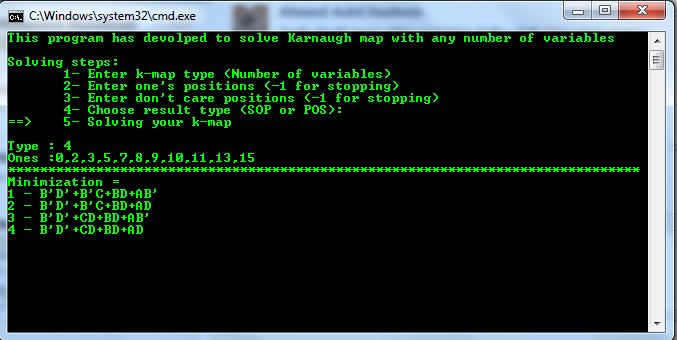
To use this program, you need to follow the next steps:

1. Enter k-map type (Number of variables)
2. Enter ones' positions (-1 for stopping)
3. Enter don't-care positions (-1 for stopping)
4. Choose result's type (SOP or POS)
5. Getting the solutions of your k-map 

Algorithm 

This algorithm has 3 steps. A special class is used to implement each:  

1. Setting k-map by getting its information from user (type ones' and don't care's positions) and saving ones' and don't care's positions with its Binary values.  
2. Comparing ones' and don't care's positions to get all possible minimums.
3. Filtering the comparison result to eliminate unessential terms, take essential ones and provide all possible solutions.  

Step 1  

In this step, k-map's type is entered by the user (ones' and don't care's positions). Then it's converted to its binary equivalent, i.e., its binary representation according to the k-map type. Then it's saved in a vector, so if we have a 4-var k-map, its ones' positions are 0,1,3,4 and 11 and its don't care position is 5, this leads to:  

• type will be: 4  
• ones' positions will be saved as: 0000 , 0001, 0011, 0100 and 1011
• don't care position will be saved as: 0101

Step 2  

In this step, ones and don't cares are compared by their equivalent binary values one by one:

1. If there are two Binary values matched in type - 1 digits, save this value and consider the different condition = -1.  
2. Consider all these semi-matched values as dashed values.
3. Do this process type times as if we have n-var k-map and this k-map is full, we need to do comparison n times in order to consider 1 var as -1 in each circle and at last solve this k-map with a full k-map.  

So if we follow this approach with the example mentioned in the first step, handled data will be: 

•   starting :             0000, 0001, 0011, 0100, 0101 and 1011  
•   First circle:          000(-1), 0(-1)00, 00(-1)1,0(-1)01,(-1)011 and 010(-1) 
•   Second circle:      0(-1)0(-1), 0(-1)0(-1), 00(-1)1 and (-1)011  
•   Third circle :        0(-1)0(-1), 0(-1)0(-1), 00(-1)1 and (-1)011    
•   Last circle:           0(-1)0(-1), 0(-1)0(-1), 00(-1)1 and (-1)011      

After comparison, repeated terms are deleted to ensure the ease of the next process. So, the data which will be handled then is: 0(-1)0(-1), 00(-1)1 and (-1)011. 

After deletion, binary terms are converted to their equivalent alphabetical letters with the following instructions:    

1. These numerical terms are represented with letters equal to its type's value, starting with A then B,C ... etc.  
2. First digit from the left represents A, the second is B, the third is C ... etc.
3. If the digit equals 0, its equivalent letter will be dashed. If it equals 1 it won't be dashed and if it equals (-1) then it will be skipped.  

So, the last binary values would be represented by: A'C', A'B'D and B'CD.

Note: If all the min-terms of a term : -1, this means a full map, and its solution = 1 , and if there aren't any ones, this means an empty map and its solution will be 0. And in these cases, the next step (filter) will be skipped.

Step 3

In this step, results that came from comparison are filtered as these results aren't all essential. And finding all possible solutions is attempted using next instructors:

1. Count all term's min-terms and set the largest term's min-term's count.
2. Assume all smaller term's min-terms as essential terms.
3. Make a combination between essential terms and other terms and check them. If they accept the k-map save them, otherwise don't save them until all k-map's possible solutions are saved.

Note: All possible solutions should have the same term's number.

Implementation

Step 1

In step 1, class setKmap is used. This class sets the k-map by getting its information from user (type, one's positions and don't-care's positions) and saving one's positions and don't care's positions with its binary values, as:

1. guidewin method guides user during using the program by demonstrating its processes steps.
2. readInt method is the method that is used to read integer values and -1 (if needed) and prevent unneeded inputs.
3. getPos method is the method that reads one's and don't care's positions using readInt method.
4. setTerms method is the method that saves one's and don't care's positions with its binary equivalent.

//this class is used for prompting k-map details from user
//and setting k-map in order to solveing itclass setKmap 
{ 
protected: 
		int	type,	            //k-map type 2,3, ....
			termCount,          //term's count
			saverCount;			//saving savers
		vector<int>ones;          //Saving ones position
 		vector<int>dCare;        //Saving dont care position
		bool hasEnteredType,      //check entering type of not
			SOP;			      // ture for some of product
		                          // false for product of some
	void guideWin (short cursor);
	int readInt (int &count, bool negative ); 
	void getPos (vector<int> &pos, string name);
	void setTerms (vector<int> ones, vector<vector<int> > &terms);  
	
	setKmap(): hasEnteredType(false) {}
};//end kmap 

Step 2

In this step, class CompareKmapTerms is used. This class inherits the class setKmap to compare one's positions and don't-care's positions in order to get all possible minimizings, as:

1. Minimize method is the method that performs comparison by:
   • Setting one's positions in k-map with setTerms method.
   • Setting don't-care positions in k-map with setTerms method.
   • Comparing all terms with each other in pairs using compare method.
   • Removing repeated terms with unrepeat method.
   • Convert binary terms to alphabetical symbols by posToTerm method.
2. Compare method which compares all terms one by one and if there are two terms match in digits and equal type value - 1, it saves them with saveValue method and consider the different digit = -1, and consider this term as dashed one.
3. saveValue is the method that follows compare method in saving semi-matching terms.
4. addOther is the method that saves terms which haven't been dashed.
5. unRepeat is the method that removes repeated terms after saving.
6. posToTerm is the method that converts binary terms to alphabetical term.

//This class is used to compare inputs results and provides
// minmizing terms in order to filter them and get results
class   CompareKmapTerms : public setKmap 
{
protected:
		int	temp, temp1, temp2, temp3; //temperature variables
		int resultTerms;
	vector<char> minimize (vector<int> &ones, vector<int> &dCare);
	void compare (vector < vector< int >> &terms); // comparelify
	void saveValue(vector<int> &tempSave, vector<vector<int>> 
	&saver, vector<bool> &hascompare, vector<vector<int>> &terms);
	void addOther (vector<vector<int>> &saver,vector<bool> 
	&hascompare, int &saverCount, vector<vector<int>> &terms);
	void unRepeat (vector<vector<int> > &terms);
	vector<char> posToTerm(vector<vector<int>> 
	&terms); //convert position to its terms
		
};//end kmap 

Step 3

In this step, class FilterKmapTerms is used. This class inherits classes CompareKmapTerms, ConverteTerms and Combination to filter comparison results to prevent unessential terms, take essential terms and provide all possible solutions, as:

1. getTerm is the method that can read one term from an array of characters that has some terms.
2. getMintermCount is the method that can count a term's min-terms.
3. getLargestTermSize is the method that can determine the largest term in comparison with its min-term's count.
4. checkResult is the method that checks if some result covers all ones or not.
5. getFilterResult is the method that makes a combination between unessential terms and adds them to essential terms. Then it checks this result by checkResult method, as if this result is covering all ones, it will save it till getting all possible solutions.
6. Filter is the method that organizes the class's processes by:
   • Determining largest term in min-terms by getLargestTermSize method.
   • Determining essential terms and unessential terms in comparison with its term's min-terms.
   • Making a combination between unessential terms and adding them to essential terms to create a result.
   • Checking some result with chechResult method, to determine if this result covers all ones or not, as if yes, save this result.

//this class is used for filtering results and giving
//all possible results
class FilterKmapTerms : public CompareKmapTerms, public ConverteTerms, public Combination
{
protected:
	int	temp, temp1, temp2, temp3; //temperature variables
	vector<char> getTerm (vector<char> 
	&result, int pos); //getting a term form an array
	int getMintermCount(vector<char> &term);
	int getLargestTermSize(vector<char> &result);
	bool checkResult (vector<char> someResult, vector<int> ones );	
vector <vector<char>> getFilterResult(vector<vector 
< char>> &results, vector<char> &essentialTerms);	
	vector <vector<char>> filter 
	(vector<char> &result, vector<int> ones);	
};//end filterKmapTerms 

Finally, the results are printed.

Points of Interest

1. This code deals with all types of k-maps, i.e., with any number of variables and this is the newest thing (26 variables as the number of letters in English alphabet).
2. This code depends in its work on vector templates, so it saves memory in comparison with codes that depend on arrays as vectors has been built.
3. It can deal with most irregular cases (if not all).

Reference

• Digital Design 4^th edition, by M. Morris Mano and Michael D. Ciletti