Introduction
This article provides a 2-3 tree implementation in the C++ language. The implementation is based on several articles found on the internet. These articles can be found in the references section, which also offers articles with an in-depth explanation of a 2-3 tree.
For the implementation I used a threaded tree. A threaded tree makes use of a parent pointer. This parent pointer makes it easier to move from a child node to its corresponding parent without using recursion. In addition, I used templates to enable the usage of different data types in the 2-3 tree.
Background
A 2-3 tree is a multi-way search tree in which each node has two children (referred to as a two node) or three children (referred to as a three node). A two node contains one element. The left subtree contains elements that are less than the node element. The right subtree contains elements that are greater than the node element. However unlike a binary search tree a two node can have either no children or two children it cannot have just one child. A three node contains two elements, one designated as the smaller element and one designated as the larger element. A three node has either no children or three children. If a three node has children, the left subtree contains elements that are less than the smaller node element. The right subtree contains elements greater than the larger node element. The middle subtree contains elements that are greater than the smaller node element and less than the larger node element. Due to the self balancing effect of a 2-3 tree all the leaves are on the same level. A 2-3 tree of size N has a search time complexity of O(log N).
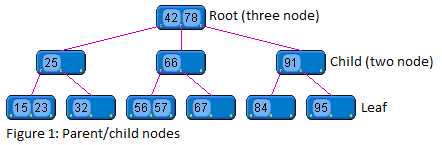
Inserting elements into a 2-3 tree
All insertions in a 2-3 tree occur at the leaves of the tree. The tree is searched to determine where the new element will go, then it is inserted. The process of inserting an element into a 2-3 tree can have a ripple effect on the structure of the rest of the tree. Inserting an element into a 2-3 tree can be divided into three cases.
- The simplest case is that the tree is empty. In this case a new node is created containing the new element. The node is then designated as the root of the tree.
- The second case occurs when we want to insert a new element at a leaf that is a 2-node. In this case the new element is added to the 2-node making it a 3-node.
- The third insertion situation occurs when we want to insert a new element at a leaf that is a 3-node. In this cases the 3-node is split and the middle element is moved up a level in the tree and the insertion process is repeated. When the root of the tree is split, the height of the tree increases by one.

Deleting elements from a 2-3 tree
Deleting elements from a 2-3 tree is also made up of three cases.
- The simplest case is that the element to be removed is in a leaf that is a 3-node. In this case, removal is simply a matter of removing the element from the node.
- The second case is that the element to be removed is in a leaf that is a 2-node. This condition is called underflow and creates a situation in which we must rotate or merge nodes in order to maintain the properties of the 2-3 tree.
- The third case is that the element to be removed is in an internal node. In this case, we can simply replace the element to be removed with its inorder successor. The inorder successor of an internal element will always be a leaf element. After replacement we can simply remove the leaf element using the first or second case.

Using the code
The project available for download includes a 2-3 tree implementation and test cases that illustrate the usage of the tree. The test cases are described in the document TreeTestcases.pdf, which is included in the project. Extract the zip file into a directory, and its ready for use. The CTree usage is straightforward. The only condition that should be met is that the key object supports the < and << operators because these two operators are used in the CTree class.
All tree functions are encapsulated in two template classes CTree and CNode. Each of the tree functions has a comment block that describes what that function does. I am avoiding recursion functions in the tree to avoid stack overflow. So you will find all my code using while loops. Due to this the code becomes a little more complicated, especially in the print function.
To create a tree object, call the default constructor:
CTree<CMovie> *pMovieTree = new CTree<CMovie>();
In order for the CTree object to make the necessary key comparisons, the key object must implement the < operator.
class CMovie
{
inline bool operator< (const CMovie& rCMovie) const
{
return (strcmp(this->getTitle(), rCMovie.getTitle()) < 0);
};
}
int CTree<T>::TCompare(const T* const pT1, const T* const pT2) const
{
int iReturnCode = FAILURE;
if(*pT1 < *pT2)
{
iReturnCode = LESS;
}
else if(*pT2 < *pT1)
{
iReturnCode = GREATER;
}
else
{
iReturnCode = EQUAL;
}
return iReturnCode;
}
In order for the CTree object to print the key objects, the key object must also implement the << operator.
friend std::ostream& operator<< (std::ostream& out, CMovie& rCMovie)
{
out <<rCMovie.getTitle()<<";"<<rCMovie.getReleaseYear();
return out;
}
Overview of public CTree functions
int insert(const T* const pKey): Inserts a new key in the tree. int deleteItem(const T* const pKey): Deletes a key and fixes the tree. const T* const find(const T* const): Searches for specified key in the tree. int print(eTreeTraversal eTraversalMethod) const: Prints all keys (inorder, postorder and preorder).int removeAll(void): Removes all tree nodes.
Output from the test project
The sample project demonstrates various method calls to the tree. The resulting output is show in a console window. Executing one of the test cases produces the following output:

Points of Interest
The tree stores (key) objects. These objects can embed key attributes (used for comparison) as well as data attributes. If we want to perform a search in the tree to find a specific object, a search object needs to be created with the comparison attributes set. The search object can then be passed to the find method, which then searches the tree and returns the object found. Examples on how to search the tree can be found in the demo project.
The templates used in the Tree classes are implemented in header files. Due to the usage of template variables, boolean flags are used to indicate which keys are set.
T m_tSmallKey;
T m_tBigKey;
bool m_bBigKeyIsSet;
bool m_bSmallKeyIsSet;
The code is well tested. A summary of the test cases used can be found in the included document TreeTestcases.pdf. Improvements that can be made to the code include, displaying the tree in a graphical format instead of a windows console, optimizing the code for speed and improving the readability of the print function.
References
