Introduction
In mathematics, the exponential function is the function ex, where e is the number (approximately 2.718281828) such that the function ex is its own derivative. The exponential function can be characterized in many ways, one of the most common characterizations is with the infinite Taylor series.
A Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point.
The concept of a Taylor series was formally introduced by the English mathematician Brook Taylor in 1715. If the Taylor series is centered at zero, then that series is also called a Maclaurin series, named after the Scottish mathematician Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century.
I implement the exponential function in two different ways, one with recursion and the other without, I used Common Table Expression; for more details about using and implementing CTE check this nice article: CTE in SQL Servers.
Implement with CTE
To find out what I do in my code, as the picture shows I need to calculate the factorial of digits and power of them, I create a table with an identity row by cte:
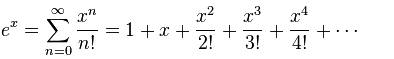
As default number of recursion in cte is 100, I limit the identity number to 100, so the series continues 100 times.
;WITH CTE AS
(SELECT cast(1.0 as float) AS rowNumber
UNION ALL
SELECT cast(cast(rowNumber as float)+1 as float)
from CTE
WHERE rowNumber < 100)
select *
FROM CTE
And the result is numbers 1 to 100:

Then for each number I need its factorial. For this I add an additional column, and it is the result of multiplication with the last rows for each row:
;WITH CTE AS
(SELECT cast(1.0 as float) AS i,
cast(1.0 as float) AS factorial
UNION ALL
SELECT cast(cast(i as float)+1 as float),
cast(cast(factorial as float)*(cast(i as float)+1)as float)
FROM CTE
WHERE i < 100)
select * from CTE And the result is as below:
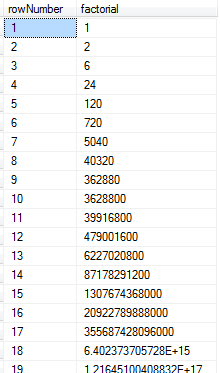
At last for each row I want the power of rowNumber for x and I use the power function.
As first the row which is created is the result of @x ^1. In the second row I start the power with rowNumber +1.
declare @x float = 3
;WITH CTE AS
(SELECT cast(1.0 as float) AS rowNumber,
cast(1.0 as float) AS factorial,
cast(@x as float)as [power]
UNION ALL
SELECT cast(cast(rowNumber as float)+1 as float),
cast(cast(factorial as float)*(cast(rowNumber as float)+1)as float),
cast(power(cast(@x as float),cast(rowNumber+1 as float)) as float)
FROM CTE
WHERE rowNumber < 100)
select * from CTE And the result is as below:
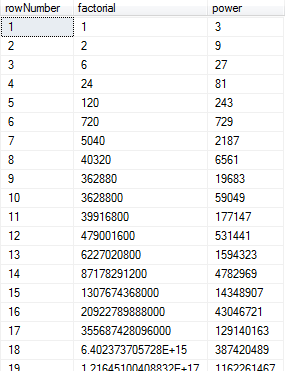
At last I added the division of power to the factorial in each row with others by dynamic concatenation:
create FUNCTION dbo.EpowerX(@x int)
RETURNS FLOAT
AS
BEGIN
declare @Result float
;WITH N AS
(SELECT cast(1.0 as float) AS i,
cast(1.0 as float) AS f,
cast(@x as float)as g
UNION ALL
SELECT cast(cast(i as float)+1 as float),
cast(cast(f as float)*(cast(i as float)+1)as float),
cast(power(cast(@x as float),cast(i+1 as float)) as float)
FROM N
WHERE i < 100)
select @Result=isnull(@Result,cast(@x as float))+ cast(g as float)/cast(f as float)
from N
where i !=1
OPTION (MAXRECURSION 0);
RETURN @Result + 1
END
select cast(cast(dbo.EpowerX(30) as float) as decimal(38,3)) as myex
select cast(cast(EXP(30)as float) as decimal(38,3)) sqlexpAnd the result is :
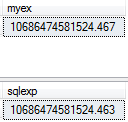
I hope it was a useful article and you enjoyed the T-SQL programming.
