Introduction
In this article, I will explain the technical architecture of Jace.NET (https://github.com/pieterderycke/Jace), an OSS framework which I developed in my spare time. Jace.NET is a high performance calculation engine for the .NET platform that can dynamically interpret and execute strings containing mathematical functions. These functions can rely on variables. If variables are used, values can be provided for these variables at execution time of the mathematical function. Jace.NET is available for the various .NET flavors: .NET, WinRT, WP7, and WP8.
Background
In a variety of applications, the need arises to have formulas specifically suited for different business case. Examples are payroll systems, scientific simulations, financial applications… Unfortunately, implementing such an engine is not a particularly straightforward task for the average programmer: the operation precedence rules make parsing mathematical formulas hard.
Quite a few developers are unaware, however, that this problem has already been tackled about five (!) decades ago by the Dutch computer scientist Edsger W. Dijkstra. He came up with the simple shunting-yard algorithm, very much inspired by the way how a railroad junction functions. This algorithm is simple and it can be explained in pseudo code on a single page.
I was not the first to develop a calculation engine for the .NET framework that allows developers to introduce dynamic formulas in their applications without being bothered with the complexity of parsing mathematical formulas. But I was confronted with the fact that the existing frameworks had design limitations that did not allow an easy port to newer .NET platforms such as Windows Phone or Windows RT. So I decided to start Jace.NET (Just another calculation for .NET) with a parser based on the shunting yard algorithm. Jace.NET offers a public API that is completely identical across all supported platforms.
Architecture
Jace.NET has an architecture similar to the one of modern compilers: interpretation and execution are performed in a number of steps. Each step focuses on one aspect of the parsing and interpretation of the formula. This keeps the overall complexity manageable.
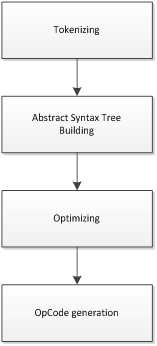
Tokenizing
The process starts with the tokenizing phase. During this phase, the input string is converted into the various allowed tokens: integers, doubles, operations and variables. If a part of the input string contains text that does not match with any type of token,
an exception is thrown and Jace will halt.
someVariable + 2 * 3 => [‘someVariable’, ‘+’, ‘2’, ‘3’]
public List<Token> Read(string formula)
{
if (string.IsNullOrEmpty(formula))
throw new ArgumentNullException("formula");
List<Token> tokens = new List<Token>();
char[] characters = formula.ToCharArray();
bool isFormulaSubPart = true;
for(int i = 0; i < characters.Length; i++)
{
if (IsPartOfNumeric(characters[i], true, isFormulaSubPart))
{
string buffer = "" + characters[i];
int startPosition = i;
while (++i < characters.Length &&
IsPartOfNumeric(characters[i], false, isFormulaSubPart))
{
buffer += characters[i];
}
int intValue;
if (int.TryParse(buffer, out intValue))
{
tokens.Add(new Token() { TokenType = TokenType.Integer,
Value = intValue, StartPosition = startPosition, Length = i - startPosition });
isFormulaSubPart = false;
}
else
{
double doubleValue;
if (double.TryParse(buffer, NumberStyles.Float | NumberStyles.AllowThousands,
cultureInfo, out doubleValue))
{
tokens.Add(new Token() { TokenType = TokenType.FloatingPoint,
Value = doubleValue,
StartPosition = startPosition, Length = i - startPosition });
isFormulaSubPart = false;
}
else if (buffer == "-")
{
tokens.Add(new Token() { TokenType = TokenType.Operation,
Value = '_', StartPosition = startPosition, Length = 1 });
}
}
if (i == characters.Length)
{
continue;
}
}
if (IsPartOfVariable(characters[i], true))
{
string buffer = "" + characters[i];
int startPosition = i;
while (++i < characters.Length && IsPartOfVariable(characters[i], false))
{
buffer += characters[i];
}
tokens.Add(new Token() { TokenType = TokenType.Text,
Value = buffer, StartPosition = startPosition, Length = i -startPosition });
isFormulaSubPart = false;
if (i == characters.Length)
{
continue;
}
}
if (characters[i] == this.argumentSeparator)
{
tokens.Add(new Token() { TokenType = Tokenizer.TokenType.ArgumentSeparator,
Value = characters[i], StartPosition = i, Length = 1 });
isFormulaSubPart = false;
}
else
{
switch (characters[i])
{
case ' ':
continue;
case '+':
case '-':
case '*':
case '/':
case '^':
case '%':
if (IsUnaryMinus(characters[i], tokens))
{
tokens.Add(new Token() { TokenType = TokenType.Operation,
Value = '_', StartPosition = i, Length = 1 });
}
else
{
tokens.Add(new Token() { TokenType = TokenType.Operation,
Value = characters[i],
StartPosition = i, Length = 1 });
}
isFormulaSubPart = true;
break;
case '(':
tokens.Add(new Token() { TokenType = TokenType.LeftBracket,
Value = characters[i], StartPosition = i, Length = 1 });
isFormulaSubPart = true;
break;
case ')':
tokens.Add(new Token() { TokenType = TokenType.RightBracket,
Value = characters[i],
StartPosition = i, Length = 1 });
isFormulaSubPart = false;
break;
default:
break;
}
}
}
return tokens;
} Abstract Syntax Tree Building
When tokenizing is successfully finished, an abstract syntax tree (AST) is constructed. This abstract syntax tree is a tree like data model that unambiguously represents the mathematical formula in memory. All mathematical precedence rules are taken into account when constructing the abstract syntax tree. Jace uses an algorithm inspired by the shunting-yard algorithm of Dijkstra to create this AST.

Optimizing
After AST creation, the optimizer will try to simplify the abstract syntax tree: if a part of the formula does not depend on variables but solely on constants. This part of the tree is already calculated and replaced by a constant in the tree.

public Operation Optimize(Operation operation, IFunctionRegistry functionRegistry)
{
if (!operation.DependsOnVariables && operation.GetType() != typeof(IntegerConstant)
&& operation.GetType() != typeof(FloatingPointConstant))
{
double result = executor.Execute(operation, functionRegistry);
return new FloatingPointConstant(result);
}
else
{
if (operation.GetType() == typeof(Addition))
{
Addition addition = (Addition)operation;
addition.Argument1 = Optimize(addition.Argument1, functionRegistry);
addition.Argument2 = Optimize(addition.Argument2, functionRegistry);
}
else if (operation.GetType() == typeof(Subtraction))
{
Subtraction substraction = (Subtraction)operation;
substraction.Argument1 = Optimize(substraction.Argument1, functionRegistry);
substraction.Argument2 = Optimize(substraction.Argument2, functionRegistry);
}
else if (operation.GetType() == typeof(Multiplication))
{
Multiplication multiplication = (Multiplication)operation;
multiplication.Argument1 = Optimize(multiplication.Argument1, functionRegistry);
multiplication.Argument2 = Optimize(multiplication.Argument2, functionRegistry);
}
else if (operation.GetType() == typeof(Division))
{
Division division = (Division)operation;
division.Dividend = Optimize(division.Dividend, functionRegistry);
division.Divisor = Optimize(division.Divisor, functionRegistry);
}
else if (operation.GetType() == typeof(Exponentiation))
{
Exponentiation division = (Exponentiation)operation;
division.Base = Optimize(division.Base, functionRegistry);
division.Exponent = Optimize(division.Exponent, functionRegistry);
}
return operation;
}
} OpCode Generation
The final phase is the OpCode generation. During this phase, a .NET dynamic method is created and the necessary MSIL is generated to execute the formula. To generate this, I rely on two advanced APIs of the .NET framework: Reflection.emit and Expression Trees. Of these two frameworks, Reflection.Emit is the oldest and the most low-level. It allows to dynamically create classes and methods by emitting the necessary MSIL instructions (MSIL is the assembler of the CLR). This framework is supported on Windows Phone and the standard .NET framework, but unfortunately not on WinRT. Expression Trees is the newer API of Microsoft to generate dynamic methods and provides an abstraction above the MSIL. Unfortunately, this API is not (yet) supported on Windows Phone.
| .NET 4.0 | WinRT | Windows Phone |
| Reflection.emit | P | O | P |
| Expression Trees | P | P | O |
The component in the Jace.NET source code responsible for the OpCode generation is called the DynamicCompiler. Two implementations of this component exist: one based on Reflection.Emit and one based on Expression Trees. Depending on the used platform, one of the two implementations is used. This is handled internally in Jace.NET and is transparent for developers using Jace.NET.
Example of Reflection.Emit
private void GenerateMethodBody(ILGenerator generator, Operation operation,
IFunctionRegistry functionRegistry)
{
if (operation == null)
throw new ArgumentNullException("operation");
if (operation.GetType() == typeof(IntegerConstant))
{
IntegerConstant constant = (IntegerConstant)operation;
generator.Emit(OpCodes.Ldc_I4, constant.Value);
generator.Emit(OpCodes.Conv_R8);
}
else if (operation.GetType() == typeof(FloatingPointConstant))
{
FloatingPointConstant constant = (FloatingPointConstant)operation;
generator.Emit(OpCodes.Ldc_R8, constant.Value);
}
else if (operation.GetType() == typeof(Variable))
{
Type dictionaryType = typeof(Dictionary<string, double>);
Variable variable = (Variable)operation;
Label throwExceptionLabel = generator.DefineLabel();
Label returnLabel = generator.DefineLabel();
generator.Emit(OpCodes.Ldarg_0);
generator.Emit(OpCodes.Callvirt,
typeof(FormulaContext).GetProperty("Variables").GetGetMethod());
generator.Emit(OpCodes.Ldstr, variable.Name);
generator.Emit(OpCodes.Callvirt, dictionaryType.GetMethod
("ContainsKey", new Type[] { typeof(string) }));
generator.Emit(OpCodes.Ldc_I4_0);
generator.Emit(OpCodes.Ceq);
generator.Emit(OpCodes.Brtrue_S, throwExceptionLabel);
generator.Emit(OpCodes.Ldarg_0);
generator.Emit(OpCodes.Callvirt,
typeof(FormulaContext).GetProperty("Variables").GetGetMethod());
generator.Emit(OpCodes.Ldstr, variable.Name);
generator.Emit(OpCodes.Callvirt,
dictionaryType.GetMethod("get_Item", new Type[] { typeof(string) }));
generator.Emit(OpCodes.Br_S, returnLabel);
generator.MarkLabel(throwExceptionLabel);
generator.Emit(OpCodes.Ldstr, string.Format(
"The variable \"{0}\" used is not defined.", variable.Name));
generator.Emit(OpCodes.Newobj,
typeof(VariableNotDefinedException).GetConstructor(new Type[] { typeof(string) }));
generator.Emit(OpCodes.Throw);
generator.MarkLabel(returnLabel);
}
else if (operation.GetType() == typeof(Multiplication))
{
Multiplication multiplication = (Multiplication)operation;
GenerateMethodBody(generator, multiplication.Argument1, functionRegistry);
GenerateMethodBody(generator, multiplication.Argument2, functionRegistry);
generator.Emit(OpCodes.Mul);
}
else if (operation.GetType() == typeof(Addition))
{
Addition addition = (Addition)operation;
GenerateMethodBody(generator, addition.Argument1, functionRegistry);
GenerateMethodBody(generator, addition.Argument2, functionRegistry);
generator.Emit(OpCodes.Add);
}
} Example of Expression Trees
private Expression GenerateMethodBody
(Operation operation, ParameterExpression contextParameter,
IFunctionRegistry functionRegistry)
{
if (operation == null)
throw new ArgumentNullException("operation");
if (operation.GetType() == typeof(IntegerConstant))
{
IntegerConstant constant = (IntegerConstant)operation;
return Expression.Convert
(Expression.Constant(constant.Value, typeof(int)), typeof(double));
}
else if (operation.GetType() == typeof(FloatingPointConstant))
{
FloatingPointConstant constant = (FloatingPointConstant)operation;
return Expression.Constant(constant.Value, typeof(double));
}
else if (operation.GetType() == typeof(Variable))
{
Type contextType = typeof(FormulaContext);
Type dictionaryType = typeof(Dictionary<string, double>);
Variable variable = (Variable)operation;
Expression getVariables = Expression.Property(contextParameter, "Variables");
Expression isInDictionaryExpression = Expression.Call(getVariables,
dictionaryType.GetRuntimeMethod("ContainsKey", new Type[] { typeof(string) }),
Expression.Constant(variable.Name));
Expression throwException = Expression.Throw(
Expression.New(typeof
(VariableNotDefinedException).GetConstructor(new Type[] { typeof(string) }),
Expression.Constant(string.Format
("The variable \"{0}\" used is not defined.", variable.Name))));
LabelTarget returnLabel = Expression.Label(typeof(double));
return Expression.Block(
Expression.IfThenElse(
isInDictionaryExpression,
Expression.Return(returnLabel, Expression.Call(getVariables,
dictionaryType.GetRuntimeMethod
("get_Item", new Type[] { typeof(string) }),
Expression.Constant(variable.Name))),
throwException
),
Expression.Label(returnLabel, Expression.Constant(0.0))
);
}
else if (operation.GetType() == typeof(Multiplication))
{
Multiplication multiplication = (Multiplication)operation;
Expression argument1 = GenerateMethodBody
(multiplication.Argument1, contextParameter, functionRegistry);
Expression argument2 = GenerateMethodBody
(multiplication.Argument2, contextParameter, functionRegistry);
return Expression.Multiply(argument1, argument2);
}
else if (operation.GetType() == typeof(Addition))
{
Addition addition = (Addition)operation;
Expression argument1 = GenerateMethodBody
(addition.Argument1, contextParameter, functionRegistry);
Expression argument2 = GenerateMethodBody
(addition.Argument2, contextParameter, functionRegistry);
return Expression.Add(argument1, argument2);
}
} The generated dynamic methods are cached in memory. If the same formula is executed again in the future with different variable values,
the interpretation steps are skipped and the dynamic method is directly executed. If the formulas of the calculations are frequently reoccurring, Jace.NET has near compiled code performance.
Using Jace.NET
The easiest way to add Jace.NET to the solution is by using NuGet. At the moment of writing the latest stable version is “0.8.3”: https://www.nuget.org/packages/Jace.
In order to start using Jace, an instance of the calculation engine class has to be created. This calculation engine will handle the interpreting of the mathematical formulas and the caching of previously used formulas. Furthermore, it allows to easily define new functions and constants. It acts as the façade above all Jace’s internal components and offers an easy API for developers.
To directly execute a given mathematical formula using the provided variables:
CalculationEngine engine = new CalculationEngine();
double result1 = engine.Calculate("1+2-3*4/5+6-7*8/9+0");
engine.AddFunction("test", (a, b) => a + b);
double result2 = engine.Calculate("test(2,3)");
Dictionary<string, double> variables = new Dictionary<string, double>();
variables.Add("variable", 2);
variables.Add("otherVariable", 4.2);
double result3 = engine.Calculate("max(sin(variable), cos(otherVariable))", variables); To build a .NET Func accepting a dictionary as input containing the values for each variable:
CalculationEngine engine = new CalculationEngine();
Func<Dictionary<string, double>,
double> formula = engine.Build("var1+2/(3*otherVariable)");
Dictionary<string, double> variables = new Dictionary<string, double>();
variables.Add("var1", 2);
variables.Add("otherVariable", 4.2);
double result = formula(variables); Jace.NET also allows to build typed Funcs:
CalculationEngine engine = new CalculationEngine();
Func<int, double, double> formula =
(Func<int, double, double>)engine.Function("var1+2/(3*otherVariable)")
.Parameter("var1", DataType.Integer)
.Parameter("otherVariable", DataType.FloatingPoint)
.Result(DataType.FloatingPoint)
.Build();
double result = formula(2, 4.2);
Further Reading
History
- 18/11/2013: Initial version
