Introduction
Tree structures are one of the most popular data structures used in today's world. They are not only effective in organizing data but provide an efficient
lookup. Implementing trees using programming languages like C, C++, Java, C#.NET and many other languages is not uncommon. However, implementing
tree like structure in database is not very popular. Here, I am first going to present a simple database schema design to store trees having N child
nodes (commonly termed as N-ary trees). Then I will explain a technique to calculate cost of the tree. Readers can extend this structure by implementing
it with various attributes as per their needs. I hope that you will find it helpful.
Background
A tree is a hierarchical structure which is derived from a single node called as root node. Each node (except leaf nodes) can have upto N children (in N-ary tree)
. Nodes that do not have any children are termed as leaf nodes. In this tutorial, we assume a tree where each node is associated with a weight.
Each link in a tree is associated with a link weight and a node's "cost" is determined as:
Node cost j = Node weight j + Sum of(Link weight of child i * Node weight of child i)
Designing the Schema
The database schema consists of two tables viz. Nodes and Links. Nodes table is designed as shown below:
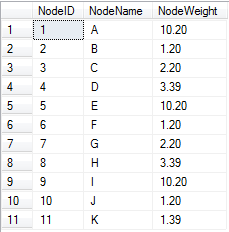
Each node consists of NodeWeight which is used for calculation of its parent node's cost. Cost is calculated using the above formula.
Links table is designed as below:

LinkWeight defines the cost of link connecting the node with its parent. The Links table shown above consists of two tree structures.
For simiplicity, I have shown the tree structure in the below image for its pictorial representation.

Motivation
Tree structures similar to which are described above are very useful in storing hierarchical data in databases. A very popular application of such schema
would be Bill of Material. However, to avoid stereotyping of this application to bill of materials, I will explain a very general design.
Such database structures can also be traversed using common tabular expressions (CTE) however, on large databases CTE can incur high computation cost. The
scheme explained in this article is lightweight since it uses Stack as the data structure to traverse the tree.
Using the Code
The algorithm shown below for calculating tree cost can be divided into two sections. The procedure accepts a node ID as input and calculates cost for that Node.
Passing root node ID will give cost for its subtree; for example, passing ID of F will generate cost for subtree rooted at F.
Let's start by creating temporary tables to store intermediate data.
Extracting Rooted Tree
CREATE PROCEDURE GetTreeCost
(
@NodeID INT
)
AS
BEGIN
CREATE TABLE #TREE
(
RecordID INT IDENTITY(1,1),
ParentNodeID INT,
NodeID INT,
NodeWeight DECIMAL(18,2),
LinkWeight INT,
LevelID INT,
ProcessingComplete BIT
)
CREATE TABLE #STACK
(
ParentNodeID INT,
NodeID INT,
LevelID INT
)
First section can be labeled as "Tree formation". Given a node id, we first extract tree structure rooted at that node in a temporary table
#TREE.
INSERT INTO #STACK
SELECT -1, @NodeID, NodeWeight FROM Nodes WHERE NodeID = @NodeID
INSERT INTO #TREE
SELECT -1, @NodeID, NodeWeight, 1, 0, 0 FROM Nodes WHERE NodeID = @NodeID
WHILE((SELECT COUNT(*) FROM #STACK) > 0)
BEGIN
SELECT TOP 1 @CurrentNodeID = NodeID, _
@CurrentParentID = ParentNodeID, @CurrentLevelID = LevelID FROM #STACK
DELETE FROM #STACK WHERE NodeID = @CurrentNodeID AND _
ParentNodeID = @CurrentParentID AND LevelID = @CurrentLevelID
IF ((SELECT COUNT(*) FROM Links L WHERE L.ParentNodeID = @CurrentNodeID) > 0)
BEGIN
INSERT INTO #STACK
SELECT @CurrentNodeID, L.NodeID, @CurrentLevelID + 1
FROM Links L WHERE L.ParentNodeID = @CurrentNodeID
INSERT INTO #TREE(ParentNodeID, NodeID, _
NodeWeight, LinkWeight, LevelID, ProcessingComplete)
SELECT @CurrentNodeID, L.NodeID, P.NodeWeight, _
L.LinkWeight, @CurrentLevelID + 1, 0 FROM Links L
INNER JOIN Nodes P ON L.NodeID = P.NodeID WHERE L.ParentNodeID = @CurrentNodeID
END
END
To extract the tree structure for a given node ID, a simple logic is used which is built on the Stack abstraction. Initially, we add the passed node ID
in Stack. Since this node is not child of any node, parent ID for this record is kept as -1. Finally, a level is maintained for tree nodes which is 0 for
root node in stack as well as tree.
Now, we iterate until there are elements present in Stack. The algorithm for extracting tree can be formulated as below:
- Pop the top node from Stack (
select and delete) - Check whether selected node is a parent node using the
Links table - If no, then continue
- Else, add children of the node in Tree as well as push them on Stack with
LevelID = CurrentLevelID + 1 - Continue
After extracting tree, #TEMP looks as shown in the below figure:

ProcessingComplete field is used during cost computation phase.
Calculating Tree Cost
Having tree ready with us in the #TREE temporary table, we can now proceed with calculating cost of the tree. Readers are advised to refer to the
formula stated above for calculating tree cost. Code for cost computation looks somewhat complicated at first, but it is eventually a simple algorithm.
WHILE((SELECT COUNT(*) FROM #TREE WHERE ProcessingComplete = 0) > 0)
BEGIN
DECLARE @MaxLevelID INT
DECLARE @RecordID INT
DECLARE @CurrentNodeWeight DECIMAL(18,2)
DECLARE @UpLinkWeight INT
SELECT @MaxLevelID = MAX(LevelID) FROM #TREE WHERE ProcessingComplete = 0
SELECT @RecordID = RecordID, @CurrentNodeID = NodeID, _
@CurrentParentID = ParentNodeID, @CurrentNodeWeight = NodeWeight,
@UpLinkWeight = LinkWeight FROM #TREE WHERE LevelID = @MaxLevelID AND ProcessingComplete = 0
IF @CurrentParentID <> -1
BEGIN
UPDATE #TREE SET NodeWeight = NodeWeight + @CurrentNodeWeight * @UpLinkWeight
WHERE NodeID = @CurrentParentID
END
UPDATE #TREE SET ProcessingComplete = 1 WHERE RecordID = @RecordID
END
ProcessingComplete field is marked when a row is processed. The algorithm proceeds in a Bottom up manner and processes nodes level wise.
We first process the leaf nodes (nodes which are at lowest level in tree, i.e., having highest level ID).
Since they are at leaf level, they do not have any children. We can compute the
cost for its parent using the formula given above. The cost update is done at the following line:
UPDATE #TREE SET NodeWeight = NodeWeight + @CurrentNodeWeight * @CurrentQuantity
WHERE NodeID = @CurrentParentID
After adding a node's cost to its parent, we mark the node as
Processed. We continue this until all the nodes in tree are processed.
Since we compute cost in bottom up manner, cost computation reaches intermediate nodes when all the nodes below its level are "Processed".
Finally, we get a fully calculated tree structure as shown in the below image:

Final cost for node 5 (E) can be seen in above figure as 106.69 which is calculated from its children.
Points of Interest
Tree structures are very simple to design and efficient to store data. A popular application of such kind of tree structure is Bill of Materials.
Using CTE approach to deal with such structures is popular, however, this handcrafted traversal of the structure makes it lightweight and cost effective.
History
