Counting and Generating Sequences

• Download source - 1 Kb

Introduction

The purpose of this post is to present some algorithmic and analytic techniques for counting and generating fixed-length sequences over some alphabet (such as bits or decimal digits).

To make the presentation more digestible, we will consider the following problems.

Problem 1: Given two positive integers n and k, where k ≤ n, count (or list) all bit strings of length n that do not contain k consecutive 1s.

Problem 2: Given two positive integers n and k, count (or list) all strings of decimal digits of length n whose sum of digits = k.

The discussion explores the use of brute-force search (augmented with pruning) for enumeration and using recurrence equations for counting and enumeration.

Also, we will discuss the use of inclusion-exclusion to solve some specific instances of these problems.

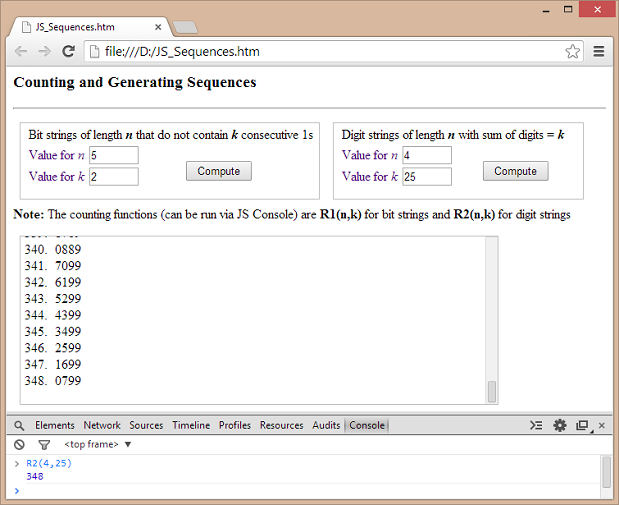
The various algorithms are encoded in JavaScript in an HTML page that can be accessed from here. The above figure shows a screen snapshot of the page when accessed from browser. Although JavaScript is slow in comparison with compiled languages, the browser environment has the benefit of quick development and testing.

Brute-force search augmented with pruning

Brute-force (exhaustive) search can be used to generate (enumerate) all sequences (vectors) of length n. Using this technique, sequences of length n, are generated one sequence at a time, and every sequence is tested for eligibility (i.e., whether it satisfies the problem constraints).

To generate sequences of a specified length n, we can use a process of slot filling. The sequence is represented as an array S[1..n]. Each array component S[i] represents a slot that can be filled with one value from a predefined set A. This process can be implemented by the following recursive procedure (This assumes that the array is to be filled in order from lowest-numbered slot to highest-numbered slot):

SlotFill(i,n))
{  for each value v in A
   {  fill the i-th slot in S with v;  
      if i = n then 
      { if ValidSolution(S) then Print(S); }
      else SlotFill(i+1) // SlotFill the remaining slots 
   }
}

For a more specific example, the following code will print all 2ⁿ bit strings of length n.

SlotFill(i,n))
{  for(k=0; k ≤1; k++)
   {  S[i] = k;  
      if i = n then 
      { Print(S); }
      else SlotFill(i+1) // SlotFill the remaining slots 
   }
}

It is somewhat surprising that the preceding code would indeed print all possible bit string of length n. The program first prints the sequence 00...0, and then the deepest recursive call returns and its parent call resumes and fills the nth slot with a bit value of 1 and prints the sequence 00...01, and so on.

It helps to prune early

Generally, for most problems, the search space is huge and it would take a long time to explore all of it. Therefore, it is best to avoid growing a partial solution vector the moment it is found to be violating the problem constraints.

[Note: This technique of brute-force search with pruning is known as "backtracking".]

This is normally achieved using a helper function, <em>ValidSolution<em>(), to test partial solution vectors for compliance with the problem's constraints.

Thus, the previous skeleton code for brute-force search can be revised into the following code (Assume that each slot is to be filled with the integers from 1 to k, and that the solution vector is defined using a global array, S[1..n].)

void SlotFill(int pos, int n)  
{ for slotval = 1 to k
  { if (sf_flag) return; // to terminate if only one solution is desired
    S[pos] = slotval; // Fill the slot at position pos 
    if ValidSolution(S,pos) // Check if partial solution S[1..pos] is valid
    { // Check if solution is complete
      if (pos == n) // Solution found 
      { sf_flag = true; Print(S); } 
      else // "pos < n" is implied; Advance to next slot
      SlotFill(pos+1,n); 
    }
  }        
}

As an alternative to testing partial vectors, we can achieve pruning by filtering the set of possible values at the time of filling a slot. For Problem 1, this means the following: at the time of filling a slot with "1", we check the previous k-1 positions and bypass the filling if we find that the previous k-1 bits are all 1s.

Based on the preceding idea, the following listing shows the program code for solving Problem 1 using Brute-force search with pruning:

// Sample initial call: SlotFill_Bits(1,10,3) to generate
// bit strings of length 10 not containing 3 consecutive 1s 
var S;  // the array object
function SlotFill_Bits(pos, n, k)  
{  for(var slotval = 0;  slotval < 1; slotval++)
   { if ((slotval==1) && (pos >= k))
        if (Filter(S,pos,k)) continue;

    S[pos] = slotval; // Fill the slot at position pos  
    {  // Check if solution is complete
       if (pos == n) // Solution found 
       { Print(S); }  
       else SlotFill_Bits(pos+1,n,k); 
    } 
  }        
}

function Filter(S,pos,k)
{   // check if any of the previous k-1 positions is 0
    for(var i=pos-1; i > pos-k; i--)   
    { if (S[i] ==0) return false; }
 
    return true; 
}

var OutStr=""; // Output vector as a string of list items
function Print(S)
{ OutStr += "<li>" + S.join("") + "</li>"; }

Using Recurrence Equations

This approach is particularly useful for counting strings. It can be used for enumeration too. As an aid to understanding this technique, we go through an example (a special case of Problem 1 with k=2).

Example 1: Derive the necessary recurrence equation(s) for R(n), the number of bit strings of length n that do not contain two consecutive 1s.

Proof:

As before, a bit string of length n can be represented by the 0/1-array S[1..n].
Let R(n) denote the number of bit strings of length n that do not contain two consecutive 1s. Let us try to relate R(n) to R(n-1) (or, in general, to R(k) where k < n). Consider the two cases of filling the leftmost slot, as illustrated in the above figure. If this slot is filled with 0, the remaining n-1 slots must not contain two consecutive 1s; by definition, the number of such strings is R(n-1). On the other hand, if the leftmost slot is filled with 1, the next slot can only be filled with 0 (to avoid consecutive 1s), and the remaining n–2 slots must not contain two consecutive 1s; the number of such strings is given by R(n-2). Therefore, we conclude that R(n) = R(n-1) + R(n-2) (Recall the sum rule, |A∪B| = |A|+|B|-|A∩B|, where in this case A∩B is the empty set.)

We need two base steps. R(1) = 2, because both binary strings of length 1 are acceptable. Also, R(2) = 3, because we are to count the strings 00, 01 and 10. Based on the preceding analysis, we can write the following recursive method to compute R(n):

// The function R returns the number of bit strings of length n 
// that do not contain two consecutive 1s 
function R(n) 
{  if (n == 1) return 2;
   else if (n == 2) return 3;
   else return R(n-1)+R(n-2);
}

Caution: The preceding function will take a long time (days) to complete for n > 30. This is caused by the presence of the two recursive calls R(n-1) and R(n-2), which leads to an excessive number of procedure calls; certain calls with the same input arguments will be encountered more than once (for example, in computing R(4), R(2) is called twice). This problem can be resolved by converting recursion into iteration, as given by the following code.

function R_Iterative(n) 
{  if (n == 1) return 2;
   else if (n == 2) return 3;

   var A = new Array();
   A[0]=2;
   A[1]=3; 
   for(var i=2; i < n; i++)
   { A[i%2] = A[(i-1)%2] + A[(i-2)%2]; }

   return A[(n-1)%2] ;
}

Example 2: Derive the necessary recurrence equation(s) for R(n,k), the number of bit strings of length n that do not contain k (where k ≤ n) consecutive 1s.

Proof:

Consider the bit strings starting with 0 or 10 or 110, ..., or 11..10 (i.e., starting with k-1 1s). For the remaining bits in these strings we must not have k consecutive 1s. Because these strings are all of the strings that are to be counted [Note: Any string starting with k consecutive 1s must be excluded.], we conclude the following recurrence equation for R(n,k):

R(n,k) = R(n-1,k) + R(n-2,k) + ... + R(n-k,k)

As base steps, we can argue the following equations:
1. If n < k then R(n,k) = 2ⁿ, because all bit strings of length less than k are acceptable
2. If n = k then R(n,k) = 2ⁿ -1, because for n=k, we only need to exclude exactly one string (the string with k 1s).

The preceding equations can be encoded as the following JavaScript function: (It is named R1 in our JavaSCript code to distinguish it from other functions.)

// The function R1(n,k) returns the number of bit strings of length n 
// that do not contain k consecutive 1s 
function R1(n,k) 
{  if (n < k) return Math.pow(2,n);
   else if (n == k) return Math.pow(2,n)-1;
   else
   {  var sum =0;
      for(var i = 1; i ≤ k; i++)
      { sum += R1(n-i,k); }
 
      return sum; 
   }
}

Enumeration from Recurrence

If you think deeply about the recurrence equation for Example 1 (or Example 2), you might be pondering the following thought: “Can’t we use the recurrence for the number of solutions to generate the actual solutions?” This is indeed the case, and we state it as a principle.

The Enumeration Principle: The recurrence equation(s) for the number of solutions can be recast into an algorithm to generate the actual solutions.

Moreover, this approach, because it generates the solutions that satisfy the constraints and no other solutions, is expected to be more efficient than the approach that generates a larger set of solutions and filters.

Recasting the Recurrence of Example 1 into Enumeration

For the program code, we simply encode slot filling as a recursive method mimicking the process (and accompanying proof) illustrated in Figure ‎1.

We will assume that the solution vector is encoded by a global 0/1-array S[1..n]. Thus, we can do with a single input parameter n that denotes the position of the current slot to be filled. Filling starts from the n-th slot downward until we reach the first slot. When this happens, we have a completed solution vector, which we print.

// The function SlotFill_Rec(n) prints bit strings of length n that
// do not contain two consecutive 1s
// Initial call: SlotFill_Rec(n), where n is the length of binary strings   
// Uses a global array S[1..n]
function SlotFill_Rec(n) 
{ if (n == 1) 
  { S[1]=0; Print(S); S[1]=1; Print(S); }
  else if (n == 2)
  { S[1]=0; S[2]=0; Print(S); 
    S[1]=0; S[2]=1; Print(S); 
    S[1]=1; S[2]=0; Print(S);
  }
  else 
  { S[n]=0; SlotFill_Rec(n-1);
    S[n]=1; S[n-1]=0; SlotFill_Rec(n-2);
  } 
}

Recurrence and Enumeration for Problem 2

We present this as one more example.

Example 3: Derive recurrence equation(s) for R(n,k) as defined in Problem 2. Use the equations to write a program function for generating the corresponding strings.

Proof for recurrence:

Let R(n,k) denote the number of strings of decimal digits of length n whose sum of digits = k. If the leftmost slot is filled with digit d, the remaining n-1 slots must have their sum of digits = k-d; by definition, the number of such strings is R(n-1,k-d). Because there are 10 possible values for filling the leftmost slot, it follows that R(n,k) = R(n-1,k) + R(n-1,k-1) + ... + R(n-1,k-9)

As base steps we have R(1,k) = 1 if k is one of the digit values 0-9; otherwise, R(1,k) = 0.

Based on the preceding proof, we can write the following recursive function to compute R(n,k) (It is named R2 in our JavaSCript code to distinguish it from other functions.)

// The function R2(n, k) returns the number of decimal 
// strings of length n whose sum of digits = k
function R2(n, k) 
{  if (n == 1)  
   {  if (( k >= 0) && (k ≤ 9)) return 1;
      else return 0; 
    }
   // else here can be committed (why?)   
   var count=0;
   for(var digit=0; digit ≤ 9; digit++)
   { count += R2(n-1, k-digit); }
   return count;
 }

The above recurrence can be expressed as the following function to enumerate the corresponding strings.

// The function SlotFill_Digits(n,k) prints decimal strings of length n 
// whose sum of digits = k
// Uses a global array S[1..n]
function SlotFill_Digits(n, k) 
{  if (n == 1)  
   {  if (( k >= 0) && (k ≤ 9))  
      { S[1]=k; Print(S); } 
   }
   else 
   for(var digit=0; digit ≤ 9; digit++)
   { S[n]= digit; SlotFill_Digits(n-1, k-digit); }
}

Other Analytic Techniques

The inclusion-exclusion principle can be utilized to produce formulas for the number of sequences satisfying certain constraints. We will show this for a specific instance of Problem 2.

Example 4:: Count all strings of decimal digits of length 4 whose sum of digits = 25.

The reader can use the hosted page (see the figure at top) to verify that the answer for this instance is 348.

The following explanation shows a solution that uses combination-with-repetition and inclusion-exclusion principle.

The number of strings (of decimal digits of length 4 whose sum of digits = 25) is equal to the number of solutions to the following equation:

X₁+ X₂+ X₃+ X₄= 25,
where the X_i's are integer variables and 0 ≤ X_i ≤ 9.

The number of solutions when X_i's are not restricted (other than X_i is non-negative) is a combination-with-repetition scenario equivalent to distributing 25 stars and 3 bars (one less than number of variables), which is Comb(25+3,3).

To handle the restricted problem, we utilize set complement. The set of solutions to the original problem = All (unrestricted) solutions - complement of the set of solutions where all of the X_is ≤ 9.

Thus, size-wise, we have the following equation for N (the number of solutions to the original problem):

N = |All solutions| -|A ∪ B ∪ C ∪ D| , where

A is the set of solutions where X₁ ≥ 10,
B is the set of solutions where X₂ ≥ 10,
C is the set of solutions where X₃ ≥ 10,
D is the set of solutions where X₄ ≥ 10.

By the inclusion-exclusion principle,

|A ∪ B ∪ C ∪ D| = |A|+ |B|+ |C| + |D| - [|A∩B| + |A∩C|+ |A∩D|+ |B∩C|+ |B∩D|+ |C∩D|] + [|A∩B∩C| + |A∩B∩D|+|A∩C∩D| + |B∩C∩D|] - |A∩B∩C∩D|

The individual sets A, B, C, or D correspond to one of the X_i's ≥ 10 (reserve 10 stars and distribute remaining 15 stars among four variables, Comb(15+3,3). (Note that this case occurs 4 times.)

The intersection of two sets corresponds to two of the X_i's ≥ 10 (reserve 20 stars and distribute remaining 5 stars among four variables, Comb(5+3,3). (Note that this case occurs Comb(4,2)= 6 times.)

The intersection of three sets, which corresponds to three of the X_i's ≥ 10, evaluates to 0 (because this needs a minimum of 30 stars).

Thus, we conclude that N = Comb(25+3,3) - 4×Comb(15+3,3) + 6×Comb(5+3,3) = (28*27*26)/(3*2*1) - 4×(18*17*16)/(3*2*1) + 6×(8*7*6)/(3*2*1) = 384.