Loop Unrolling over Template Arguments

• Download source code - 2.99 MB

Introduction

This article deals with loop unrolling, a technique to improve speed. For varying problem sizes, you can use integral template parameters.

Background

Loop unrolling is a great feature when writing fast code. Imagine when the loop count is small and you know it at compile time, like this:

for (int i = 0; i < 8; ++i) {
    a[i] = b[i] + c[i];
}

Most of the time, it is faster for the CPU (and GPU) to have the loop unrolled, because otherwise you have to jump every time at the } to the beginning of the loop. When the loop is unrolled, the code looks like this:

a[0] = b[0] + c[0];
a[1] = b[1] + c[1];
a[2] = b[2] + c[2];
a[3] = b[3] + c[3];
a[4] = b[4] + c[4];
a[5] = b[5] + c[5];
a[6] = b[6] + c[6];
a[7] = b[7] + c[7];

For pipelining and other issues, this is faster than the original loop. The processor can simply execute every statement in sequence, looking forward to further statements and pre-fetching the values. (Otherwise, there is a JNZ and a INC and some other assembler statements between every line.)

Getting it done

Of course, it would be horrible to write every loop like this (that's why there exists the loop statement!). Some small loops are already unrolled by the compiler. The Nvidia CUDA compiler and the IBM compiler offer the #pragma unroll or #pragma unroll N (where N is a literal constant) to advise the compiler to unroll the following loop, if it can predict its trip count. Unfortunately, they have problems with template parameters:

template <int N>
void doit() {
    #pragma unroll N
    for (int i = 0; i < N; ++i) {
        a[i] = b[i] + c[i];
    }
}

nvcc doesn't like the N at this place, and without any argument, it can't deduce the trip count, so the loop is not unrolled. The bad thing in CUDA coding is, if the access to an array is non-deterministic (like a[i] where i is not fixed), the compiler puts the array to an off chip location where the latency is about 700 times slower than on the chip (where you would access the array only by constant indexes, like a[0] = a[1] + a[2]). But I had a varying template parameter in many functions. I could have refactored it all with preprocessor macros, but that would have been awkward. So there came the Unroller:

//static unroller
template <typename Action, int Begin, int End, int Step = 1>
struct UnrollerS {
    static void step() {
        Action::action(Begin);
        UnrollerS<Action, Begin+Step, End, Step>::step();
    }
};
//end of static unroller
template <typename Action, int End, int Step>
struct UnrollerS<Action, End, End, Step> {
    static void step() { }
};

//dynamic unroller
template <typename Action, int Begin, int End, int Step = 1>
struct UnrollerD {
    static void step(Action& a) {
        a.action(Begin);
        UnrollerD<Action, Begin+Step, End>::step(a);
    }
};
//end of dynamic unroller
template <typename Action, int End, int Step>
struct UnrollerD<Action, End, End, Step> {
    static void step(Action& a) { }
};

UnrollerD and UnrollerS call their Action (either static or member function), and then loop themselves with Begin incremented, until they reach the partial specialization, where Begin == End they do nothing.

Using the code

So, if you have an action to be performed without any extra information, you declare it as a struct with a static function action(i), and give it to UnrollerS:

struct Printer {
    static void action(int i) {
        printf("%d\n", i);
    }
};

//later...

UnrollerS<Printer, 10, 20>::step();

If you have to pass some values to the Action, use UnrollerD:

struct Aassign {
    int* rhs;
    int *m;
    void action(int i) {
        m[i] = rhs[i];
    }
};

nbase<M>& operator=(int* rhs) {
    Aassign assign;
    assign.m = m_array;
    assign.rhs = rhs;
    //m_array and rhs are both of (templated) size M
    UnrollerD<Aassign, 0, M>::step(assign);
    return *this;
}

It depends on the inline capability of your compiler how far it inlines your Action. The Visual C++ compiler inlines only 2 or 4 steps, even with the inline declaration. You have to force it with __forceinline at the action and the step functions to completely unroll the loop.

Member function pointers

As stated in the previous version, here is the code for UnrollerM:

//member function unroller
template<typename Action, void (Action::*Function)(int), int Begin, int End, int Step = 1>
struct UnrollerM {
    static void step(Action& action) {
        (action.*Function)(Begin);
        UnrollerM<Action, Function, Begin+Step, End, Step>::step(action);
    }
};
//end of member function unroller
template<typename Action, void (Action::*Function)(int), int End, int Step>
struct UnrollerM<Action, Function, End, End, Step> {
    static void step(Action& action) {
    }
};

It is useful if you have different methods and don't want to create an Action for everything (also enables data sharing, but not shown here).

struct MultiFunctor {
    void twice(int i) {
        cout << 2*i << ' ';
    }
        void quad(int i) {
        cout << i*i << ' ';
    }
};

//...
MultiFunctor mfunc;
//call quad(int) from mfunc from 0 to 10
UnrollerM<MultiFunctor, &MultiFunctor::quad, 0, 10>::step(mfunc);
cout << endl;
//call twice(int) from mfunc from 20 to 0 step -2 (note, 0 is not evaluated)
UnrollerM<MultiFunctor, &MultiFunctor::twice, 20, 0, -1>::step(mfunc);

Lambda functions

The next step would be to use the new lambda functions rather then the "hard to type" member function pointers. In Visual Studio 2010, they appeared to have an anonymous type in an unknown namespace, so it was not easy to hardwire them as a template argument. Luckily, as a member function template, the compiler can itself deduce the correct type of the lambda.

template<int Begin, int End, int Step = 1>
//lambda unroller
struct UnrollerL {
    template<typename Lambda>
    static void step(Lambda& func) {
        func(Begin);
        UnrollerL<Begin+Step, End, Step>::step(func);
    }
};
//end of lambda unroller
template<int End, int Step>
struct UnrollerL<End, End, Step> {
    template<typename Lambda>
    static void step(Lambda& func) {
    }
};

When you are familiar with the new lambda syntax, this will be the most easy to use unroller:

//use it as local variable
auto lambda = [](int i){ cout << i << ' '; };
//means: from 30 to 20 backward
UnrollerL<30, 20, -1>::step(lambda);
cout << endl;

int numbers[] = {1, 22, 333, 4444, 55555};
//capture the array, and print it out (defined lambda on the fly)
UnrollerL<0, 5>::step( [&numbers] (int i) {
    cout << numbers[i] << ' ';
}
);

Performance test

The test ran on an Intel P8600 (dual core, 2.4 GHz) with the Visual Studio 2010 C++ compiler in Release mode and some optimizations. __forceinline was added to the step function in UnrollerL. For this test, I created a random histogram and wanted to create a prefix sum (for example, in statistical applications, or radix sort). You have an int-array histogram and transform it so that each entry has the sum of its values preceding. The core loop looks like this:

tmp = histogram[i] + sum;
histogram[i] = sum;
sum = tmp;

I measured three different computation methods. The first is "normal" as with a standard for loop:

int sum = 0;
int tmp;
for (int i = 0; i < N; ++i) {
    tmp = histogram[i] + sum;
    histogram[i] = sum;
    sum = tmp;
}

Second, the loop completely unrolled:

int sum = 0;
int tmp;
int* hist = histogram;
UnrollerL<0, N>::step( [&] (int i) {
    tmp = hist[i] + sum;
    hist[i] = sum;
    sum = tmp;
}
);

(Note: the histogram was out of scope, so I aliased a pointer and captured it in the lambda.) At last, something like a hybrid unrolled loop, or partial unrolled. The complete loop is not unrolled, but H iterations are hardwired so the loop has to cycle only N/H times.

template<int H>
//...
int sum = 0;
int tmp;
int *hist = histogram;
for (int i = 0; i < N; i += H) {
    UnrollerL<0, H>::step( [&] (int j) {
        tmp = hist[i+j] + sum;
        hist[i+j] = sum;
        sum = tmp;
    }
    );
}
//Note: lokes like a nested loop

In the first graph, normal, complete, and hybrid were measured in this order. The array size was 16, 32, 64, 128, 256; the hybrid unroll factor was 8:

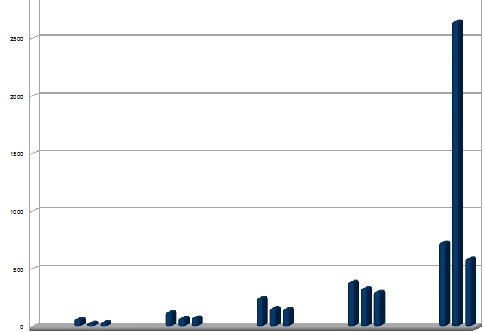
For small trip counts, complete is good. For 128 items, hybrid is already a little better. At 256 items, the complete unroll just explodes. This is because the code bloats so much, that it doesn't fit into the program cache, and is too large to be sequenced fast.

Because 256 complete unrolled iterations took so long, this type was left out in the following graph. Normal loop is left, partial unrolled right. The first three were 1024 items and hybrid unroll 8, 16, 32; the next three were 2048 with same hybrid factors; then 4096, 8192, and 16384. Then, the column sizes were halved, and 32768 was measured with 8, 16, 32, and 64 hybrid unroll. At last, 65536 was measured with 8, 16, 32, 64, and 128 inner hybrid unrolls.

Hybrid unroll is always better than the normal loop. In the last case, the raw numbers differ from 3086 to 2463.

Partial unroller

After a little praxis with the unrollers, I saw the necessity to create a partial unroller. As seen before, unrolled loops with 256 iterations are too extreme. The hybrid solution was more stable because it unrolled an inner part of the loop. It was also too strict, you have to know the total iteration count at compile time. So the solution is UnrollerP:

//UnrollerP: loops over given size, partial unrolled
template<int InnerUnroll = 8, int Begin = 0>
public:
struct UnrollerP {
    template<typename Lambda>
    static void step(size_t N, Lambda& func) {
        size_t i = Begin;
        for (; i < N - InnerUnroll; i += InnerUnroll) {
            UnrollerInternal<>::step(func, i);
        }
        for (; i < N; ++i) {
            func(i);
        }
        
    }
private:
    //start of UnrollerInternal
    template<size_t Offset = 0>
    struct UnrollerInternal {
        template<typename Lambda>
        static void step(Lambda& func, size_t i) {
            func(i + Offset);
            UnrollerInternal<Offset + 1>::step(func, i);
        }
    };

    //end of UnrollerInternal
    template<>
    struct UnrollerInternal<InnerUnroll> {
        template<typename Lambda>
        static void step(Lambda& func, size_t i) {
        }
    };

};

UnrollerP serves as a starter, the real unrolling is done by UnrollerInternal (which works as common). UnrollerP itself has a loop with InnerUnroll as increment, and in this loop body, the lambda is unrolled by this factor. For odd sizes, the last steps are iterated normally. Note that the number of total iterations N is dynamically evolved, so this is more flexible. Use it like this:

int numbers;
//get 'numbers' at runtime

int *arr = new int[numbers];
//assign some values

int sum = 0, tmp;

//unroll the loop 8 times, offset is 0 so 
//the range is from 0 to numbers
UnrollerP<8>::step(numbers, [&] (size_t i) {
    arr[i] = i;
    tmp = arr[i] + sum;
    arr[i] = sum;
    sum = tmp;
}
);

Unification

Thanks to UsYer, who figured out that UnrollerS, UnrollerD, UnrollerM, and UnrollerL can be combined to a single, STL-compliant template:

template<int Begin, int End, int Step = 1>
struct Unroller {
    template<typename Action>
    static void step(Action& action) {
        action(Begin);
        Unroller<Begin+Step, End, Step>::step(func);
    }
};

template<int End, int Step>
struct Unroller<End, End, Step> {
    template<typename Action>
    static void step(Action& action) {
    }
};

The only requirement for Action is that it must be callable, so any function or functor with operator()(int) fits. The previous examples could work like this:

int numbers[] = {1, 22, 333, 4444, 55555};

//use a free or static function:
Unroller<10, 20, 2>::step(Printer::act);

//use a functor:    
ArrayPrinter ap;
ap.items = numbers;
Unroller<1, 4>::step(ap);

//Unroll memberfunction with the help of c++1x's std::bind 
MultiFunctor mfunc;
Unroller<20,0,-1>::step(std::bind(&MultiFunctor::twice,&mfunc,std::placeholders::_1));

//Of course lambdas are supported as well, because they are callable too(std::function)
Unroller<0, 5>::step([&numbers](int i){cout << numbers[i] << ' ';});

Conclusion

Loop unrolling is a fancy tool to get several percent speedup. If you overdo it (too large trip count), your code might get slower (program code doesn't fit into the L1 cache). Just test it out, and feel the difference. With these templates, you can unleash the power and keep the maintainability.

History

• v2.1: Added partial unrolling and unifying some unrollers, thanks to UsYer.
• v2.01: Sample project can be downloaded.
• v2.0: Added support for lambda functions, performance test, and sample project.
• v1.1: Added member function pointers and variable step count.
• v1.0: Initial version.