Code Repository
Introduction
In this article we jump straight to the implementation of the algorithm, I assume reader is familiar with the Travelling salesman problem and Dynamic Programming.
Background
I couldn't find a solid implementation of the algorithm, So I decided to do it myself, hope it helps somebody ;)
How it works
The gist of dynamic programming is two parts:
1) A base case that we already know the answer of (stopping condition)
2) Decreasing the problem domain and calling our algorithm again. (Recursion)
put very simply, and without going into much mathematical lingo, the algorithm takes two inputs, the vertex we are starting from v<code>ertex, and a list of vertices to visit vertices.
No we are faced with two situations, either:
- vertices is empty, then yay! no work to do, return the distance between starting point and
<span style="font-size: 14px;">v</span><span style="font-size: 14px; color: rgb(153, 0, 0); font-family: Consolas, 'Courier New', Courier, mono;">ertex</span><span style="color: rgb(17, 17, 17); font-family: 'Segoe UI', Arial, sans-serif;">.</span> - vertices is not empty, hmph! lets decrease our problem space:
a) consider each vertex newV in vertices as a starting point.
b) since we are considering newV as a starting point, we have to adjust the list of vertices to visit, by removing newV from vertices. (why would I plan a route to a city I am already in) let it be newVertices.
c) calculate cost of visiting newV + cost of visiting rest of vertices starting from newV.
(which is basically calling the algorithm again but with newV and newVertices as input)
d) return minimum result from step c.
Step by step walkthrough
lets say we have a bi-directional graph with the following distance matrix:
| | 1 | 2 | 3 | 4 |
| 1 | 0 | 10 | 15 | 20 |
| 2 | 5 | 0 | 9 | 10 |
| 3 | 6 | 13 | 0 | 12 |
| 4 | 8 | 8 | 9 | 0 |
the starting vertex is (1), we wish to visit vertices {2,3,4}
lets say our function is called g, then what we want is:
g(1,{2,3, 4})
These are broken down into getting minimum of:
c12 + g(2,{3, 4})
c13 + g(3,{2,4})
c14 + g(4,{2,3})}
c12 is cost of getting from (1) to (2), c13 is cost of getting from (1) to (3),etc...
which are (in order)
g(2, {3,4})= min {
c23 + g(3,{4}),
c24 + g(4,{3})
} = 25
g(3, {4}) = c34 + g(4,{}) = 12 + 8 = 20
g(4, {3}) = c43 + g(3,{}) = 9 + 6 =15
g(3, {2,4})= min {
c32 + g(2,{4}),
c34 + g(4,{2})
} = 25
g(2, {4}) = c24 + g(4, {}) = 10 + 8 = 18
g(4, {2}) = c42 + g(2,{}) = 8 + 5 = 13
g(4, {2,3})= min {
c42 + g(2,{3}),
c43 + g(3,{2})
} = 23
g(3, {2}) = c32 + g(2,{}) = 13 + 5 = 18
g(2, {3}) = c23 + g(3, {}) = 9 + 6 = 15
Substituting in our first three formulas gives :
min{
10 + 25,
15 + 25,
20 + 23
}=min {35, 40, 43}=35
To get the actual tour, we create a Tree
private class Node
{
public int Value { get; set; }
public Node[] ChildNodes { get; set; }
public bool Selected { get; set; }
}
The tree data structure will mimic the branching of our algorithm, marking each time the Node (Vertex) with least cost as selected.
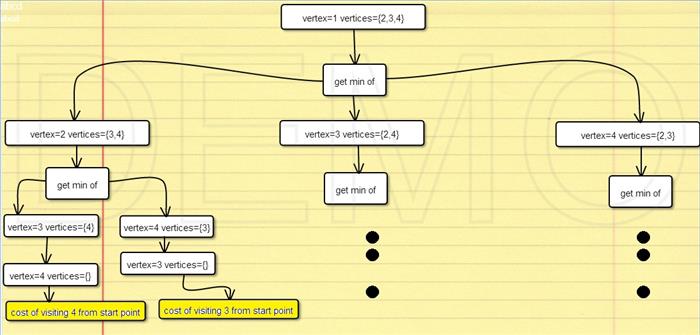
After the algorithm terminates, we traverse the tree, checking only vertices that were marked as selected.
Code
private double GetMinimumCostRoute(int startVertex, HashSet<int> set, Node root)
{
if (!set.Any())
{
root.ChildNodes = new Node[1] { new Node { Value = _vertices.First(), Selected = true } };
return _adjacencyMatrix[startVertex, 0];
}
double totalCost = double.MaxValue;
int i = 0;
int selectedIdx = i;
root.ChildNodes = new Node[set.Count()];
foreach (var destination in set)
{
root.ChildNodes[i] = new Node { Value = destination };
double costOfVistingCurrentNode = _adjacencyMatrix[startVertex, destination];
var newSet = new HashSet<int>(set);
newSet.Remove(destination);
double costOfVisitingOtherNodes = GetMinimumCostRoute(destination, newSet, root.ChildNodes[i]);
double currentCost = costOfVistingCurrentNode + costOfVisitingOtherNodes;
if (totalCost > currentCost)
{
totalCost = currentCost;
selectedIdx = i;
}
i++;
}
root.ChildNodes[selectedIdx].Selected = true;
return totalCost;
}
</int></int>
Conclusion
Note that the running time is exponential, There are at most O(n*2n) subproblems, and each one takes linear time to solve. The total running time is therefore O(n2*2n).
As always I hope I delivered a clear explanation and an adequate implementation ;)
Do let me know if you have any feedback/questions.
