Interpolate 2D Points Using Bezier Curves in WPF

• Download sample - 132.9 KB
• Sample on GitHub (WPF)
• Sample on Github (JavaScript)
• Live example in JavaScript (ReactJs)

Introduction

Interpolating points sometimes is hard mathematical work, even more, if the points are ordered. The solution is to create a function using the points and using an extra parameter t that represents the time dimension. This often is called a parametric representation of the curve. This article shows a simple way of interpolating a set of points using Bezier curves in WPF.

Background

The idea of this solution comes after asking this question in Stack Overflow. The accepted answer makes references to a simple and interesting method proposed by Maxim Shemanarev, where the control points are calculated from the original points (called anchor points).

Here, we create a WPF UserControl that draws the curve from any collection of points. This control can be used with the pattern MVVM. If any point's coordinate changes, the curve also will change automatically. For instance, it can be used for a draw application, where you can drag & drop the points for changing the drawing, or curve.

The Algorithm Behind

Due to the original antigrain site being down (I can find that Sourceforge is still supporting this library and we can find the original article over here!), I'm going to explain what is the algorithm proposed by Maxim Shemanarev.

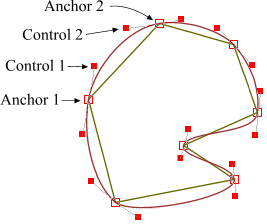A Bezier curve has two anchor points (begin and end) and two control ones (CP) that determine its shape. Our anchor points are given, they are pair of vertices of the polygon. The question is, how to calculate the control points? It is obvious that the control points of two adjacent edges form one straight line along with the vertex between them.

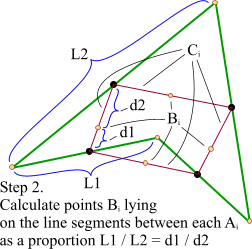
The solution found is a very simple method that does not require any complicated math. First, we take the polygon and calculate the middle points A_i of its edges.

Here, we have line segments C_i that connect two points A_i of the adjacent segments. Then, we should calculate points B_i as shown in this picture.

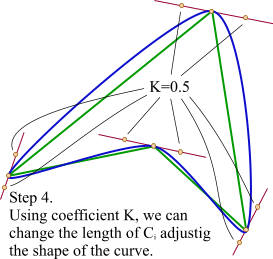
The third step is final. We simply move the line segments C_i in such a way that their points B_i coincide with the respective vertices. That's it, we calculated the control points for our Bezier curve and the result looks good.

One little improvement. Since we have a straight line that determines the place of our control points, we can move them as we want, changing the shape of the resulting curve. I used a simple coefficient K that moves the points along with the line relative to the initial distance between vertices and control points. The closer the control points to the vertices are, the sharper figure will be obtained.

The method works quite well with self-intersecting polygons. The examples below show that the result is pretty interesting.

The Class for Calculation

Below is the class that makes the calculation of the spline segments, based on the algorithm, exposed above. This class is named InterpolationUtils, it has a static method (named InterpolatePointWithBezierCurves) that returns a list of BezierCurveSegment, that will be the solution to our problem.

The class BezierCurveSegment has the four properties that define a spline segment: StartPoint, EndPoint, FirstControlPoint, and the SecondControlPoint.

As the above algorithm is originally implemented for closed curves, and it is desired that it can be applied for open curves too, a little change is needed. For this reason, the InterpolatePointWithBezierCurves method receives a second parameter, a boolean variable named isClosedCurve, which determines if the algorithm will return an open or closed curve. Since we take four points (x1 = the current point, x2 = the next point, but also are required two more points for creating the three edges. x0 = the current's previous point and x3 = the next's next point), the x0 and x3 points selection will be like this:

• If it is a closed curve if x1 is the first point, then x0 is going to be the latest point (in this implementation, it is the latest but one because the latest point is the same that the first one), and if x2 is the latest point, then x3 is going to be the first point (in a similar way, in this implementation, is going to be the second point).
• If it is an open curve, then x0 = x1 and x3 = x2 for the previous cases.

using System;
using System.Collections.Generic;
using System.Linq;
using System.Windows;

namespace BezierCurveSample.View.Utils
{
    public class InterpolationUtils
    {
        public class BezierCurveSegment
        {
            public Point StartPoint { get; set; }
            public Point EndPoint { get; set; }
            public Point FirstControlPoint { get; set; }
            public Point SecondControlPoint { get; set; }
        }

        public static List<BezierCurveSegment> 
        InterpolatePointWithBezierCurves(List<Point> points, bool isClosedCurve)
        {
            if (points.Count < 3)
                return null;
            var toRet = new List<BezierCurveSegment>();

            //if is close curve then add the first point at the end
            if (isClosedCurve)
                points.Add(points.First());

            for (int i = 0; i < points.Count - 1; i++)   //iterate for points 
                                                         //but the last one
            {
                // Assume we need to calculate the control
                // points between (x1,y1) and (x2,y2).
                // Then x0,y0 - the previous vertex,
                //      x3,y3 - the next one.
                double x1 = points[i].X;
                double y1 = points[i].Y;

                double x2 = points[i + 1].X;
                double y2 = points[i + 1].Y;

                double x0;
                double y0;

                if (i == 0) //if is first point
                {
                    if (isClosedCurve)
                    {
                        var previousPoint = points[points.Count - 2];    //last Point, 
                                            //but one (due inserted the first at the end)
                        x0 = previousPoint.X;
                        y0 = previousPoint.Y;
                    }
                    else    //Get some previouse point
                    {
                        var previousPoint = points[i];//if is the first point 
                                                      //the previous one will be itself
                        x0 = previousPoint.X;
                        y0 = previousPoint.Y;
                    }
                }
                else
                {
                    x0 = points[i - 1].X;     //Previous Point
                    y0 = points[i - 1].Y;
                }

                double x3, y3;

                if (i == points.Count - 2)    //if is the last point
                {
                    if (isClosedCurve)
                    {
                        var nextPoint = points[1];  //second Point(due inserted 
                                                    //the first at the end)
                        x3 = nextPoint.X;
                        y3 = nextPoint.Y;
                    }
                    else    //Get some next point
                    {
                        var nextPoint = points[i + 1];  //if is the last point 
                                              //the next point will be the last one
                        x3 = nextPoint.X;
                        y3 = nextPoint.Y;
                    }
                }
                else
                {
                    x3 = points[i + 2].X;   //Next Point
                    y3 = points[i + 2].Y;
                }

                double xc1 = (x0 + x1) / 2.0;
                double yc1 = (y0 + y1) / 2.0;
                double xc2 = (x1 + x2) / 2.0;
                double yc2 = (y1 + y2) / 2.0;
                double xc3 = (x2 + x3) / 2.0;
                double yc3 = (y2 + y3) / 2.0;

                double len1 = Math.Sqrt((x1 - x0) * 
                              (x1 - x0) + (y1 - y0) * (y1 - y0));
                double len2 = Math.Sqrt((x2 - x1) * 
                              (x2 - x1) + (y2 - y1) * (y2 - y1));
                double len3 = Math.Sqrt((x3 - x2) * 
                              (x3 - x2) + (y3 - y2) * (y3 - y2));

                double k1 = len1 / (len1 + len2);
                double k2 = len2 / (len2 + len3);

                double xm1 = xc1 + (xc2 - xc1) * k1;
                double ym1 = yc1 + (yc2 - yc1) * k1;

                double xm2 = xc2 + (xc3 - xc2) * k2;
                double ym2 = yc2 + (yc3 - yc2) * k2;

                const double smoothValue = 0.8;
                // Resulting control points. Here smooth_value is mentioned
                // above coefficient K whose value should be in range [0...1].
                double ctrl1_x = xm1 + (xc2 - xm1) * smoothValue + x1 - xm1;
                double ctrl1_y = ym1 + (yc2 - ym1) * smoothValue + y1 - ym1;

                double ctrl2_x = xm2 + (xc2 - xm2) * smoothValue + x2 - xm2;
                double ctrl2_y = ym2 + (yc2 - ym2) * smoothValue + y2 - ym2;
                toRet.Add(new BezierCurveSegment
                {
                    StartPoint = new Point(x1, y1),
                    EndPoint = new Point(x2, y2),
                    FirstControlPoint = i == 0 && !isClosedCurve ? 
                                        new Point(x1, y1) : new Point(ctrl1_x, ctrl1_y),
                    SecondControlPoint = i == points.Count - 2 && 
                    !isClosedCurve ? new Point(x2, y2) : new Point(ctrl2_x, ctrl2_y)
                });
            }

            return toRet;
        }
    }
} 

The User Control

The user control that we propose is very simple to use, and it works with the MVVM pattern.

The LandMarkControl has only two dependency properties, one for the points, and another for the color of the curve. The most important property is the Points attached property. It is of IEnumerable type, and it assumes that each item has an X and Y properties.

In case the collection of points implements the INotifyCollectionChanged interface, the control will register to the CollectionChanged event, and if each point implements the INotifyPropertyChanged interface, the control also will register to the PropertyChanged event. In this way, every time any point is added or removed, or any point's coordinates changed, the control will be refreshed.

This is the complete user control code behind:

using System.Collections;
using System.Collections.Generic;
using System.Collections.Specialized;
using System.ComponentModel;
using System.Linq;
using System.Windows;
using System.Windows.Controls;
using System.Windows.Media;
using BezierCurveSample.View.Utils;

namespace BezierCurveSample.View
{
    /// <summary>
    /// Interaction logic for LandmarkControl.xaml
    /// </summary>
    public partial class LandmarkControl : UserControl
    {
        #region Points

        public IEnumerable Points
        {
            get { return (IEnumerable)GetValue(PointsProperty); }
            set { SetValue(PointsProperty, value); }
        }

        // Using a DependencyProperty as the backing store for Points. 
        // This enables animation, styling, binding, etc...
        public static readonly DependencyProperty PointsProperty =
            DependencyProperty.Register("Points", typeof(IEnumerable),
            typeof(LandmarkControl), 
            new PropertyMetadata(null, PropertyChangedCallback));

        private static void PropertyChangedCallback(DependencyObject dependencyObject,
        DependencyPropertyChangedEventArgs dependencyPropertyChangedEventArgs)
        {
            var landmarkControl = dependencyObject as LandmarkControl;
            if (landmarkControl == null)
                return;

            if (dependencyPropertyChangedEventArgs.NewValue is INotifyCollectionChanged)
            {
                (dependencyPropertyChangedEventArgs.NewValue as
                INotifyCollectionChanged).CollectionChanged += 
                                          landmarkControl.OnPointCollectionChanged;
                landmarkControl.RegisterCollectionItemPropertyChanged
                (dependencyPropertyChangedEventArgs.NewValue as IEnumerable);
            }

            if (dependencyPropertyChangedEventArgs.OldValue is INotifyCollectionChanged)
            {
                (dependencyPropertyChangedEventArgs.OldValue as
                INotifyCollectionChanged).CollectionChanged -= 
                                          landmarkControl.OnPointCollectionChanged;
                landmarkControl.UnRegisterCollectionItemPropertyChanged
                (dependencyPropertyChangedEventArgs.OldValue as IEnumerable);
            }

            if (dependencyPropertyChangedEventArgs.NewValue != null)
                landmarkControl.SetPathData();
        }

        #endregion

        #region PathColor

        public Brush PathColor
        {
            get { return (Brush)GetValue(PathColorProperty); }
            set { SetValue(PathColorProperty, value); }
        }

        // Using a DependencyProperty as the backing store for PathColor. 
        // This enables animation, styling, binding, etc...
        public static readonly DependencyProperty PathColorProperty =
            DependencyProperty.Register("PathColor", typeof(Brush), 
                                         typeof(LandmarkControl),
                                         new PropertyMetadata(Brushes.Black));

        #endregion

        #region IsClosedCurve

        public static readonly DependencyProperty IsClosedCurveProperty =
            DependencyProperty.Register("IsClosedCurve", typeof (bool), 
                                         typeof (LandmarkControl),
                                         new PropertyMetadata(default(bool), 
                                         OnIsClosedCurveChanged));

        private static void OnIsClosedCurveChanged
        (DependencyObject dependencyObject, 
         DependencyPropertyChangedEventArgs dependencyPropertyChangedEventArgs)
        {
            var landmarkControl = dependencyObject as LandmarkControl;
            if (landmarkControl == null)
                return;
            landmarkControl.SetPathData();
        }

        public bool IsClosedCurve
        {
            get { return (bool) GetValue(IsClosedCurveProperty); }
            set { SetValue(IsClosedCurveProperty, value); }
        }

        #endregion


        public LandmarkControl()
        {
            InitializeComponent();
        }

        void SetPathData()
        {
            if (Points == null) return;
            var points = new List<Point>();

            foreach (var point in Points)
            {
                var pointProperties = point.GetType().GetProperties();
                if (pointProperties.All(p => p.Name != "X") ||
                pointProperties.All(p => p.Name != "Y"))
                    continue;
                var x = (float)point.GetType().GetProperty("X").GetValue
                        (point, new object[] { });
                var y = (float)point.GetType().GetProperty("Y").GetValue
                        (point, new object[] { });
                points.Add(new Point(x, y));
            }

            if (points.Count <= 1)
                return;

            var myPathFigure = new PathFigure { StartPoint = points.FirstOrDefault() };


            var myPathSegmentCollection = new PathSegmentCollection();

            var bezierSegments = InterpolationUtils.InterpolatePointWithBezierCurves
                                 (points, IsClosedCurve);

            if (bezierSegments == null || bezierSegments.Count < 1)
            {
                //Add a line segment <this is generic for more than one line>
                foreach (var point in points.GetRange(1, points.Count - 1))
                {

                    var myLineSegment = new LineSegment { Point = point };
                    myPathSegmentCollection.Add(myLineSegment);
                }
            }
            else
            {
                foreach (var bezierCurveSegment in bezierSegments)
                {
                    var segment = new BezierSegment
                    {
                        Point1 = bezierCurveSegment.FirstControlPoint,
                        Point2 = bezierCurveSegment.SecondControlPoint,
                        Point3 = bezerCurveSegment.EndPoint
                    };
                    myPathSegmentCollection.Add(segment);
                }
            }

            myPathFigure.Segments = myPathSegmentCollection;

            var myPathFigureCollection = new PathFigureCollection {myPathFigure} ;

            var myPathGeometry = new PathGeometry { Figures = myPathFigureCollection };

            path.Data = myPathGeometry;
        }

        private void RegisterCollectionItemPropertyChanged(IEnumerable collection)
        {
            if (collection == null)
                return;
            foreach (INotifyPropertyChanged point in collection)
                point.PropertyChanged += OnPointPropertyChanged;
        }

        private void UnRegisterCollectionItemPropertyChanged(IEnumerable collection)
        {
            if (collection == null)
                return;
            foreach (INotifyPropertyChanged point in collection)
                point.PropertyChanged -= OnPointPropertyChanged;
        }

        private void OnPointCollectionChanged(object sender, 
                                              NotifyCollectionChangedEventArgs e)
        {
            RegisterCollectionItemPropertyChanged(e.NewItems);

            UnRegisterCollectionItemPropertyChanged(e.OldItems);

            SetPathData();
        }

        private void OnPointPropertyChanged(object sender, PropertyChangedEventArgs e)
        {
            if (e.PropertyName == "X" || e.PropertyName == "Y")
                SetPathData();
        }
    }
} 

And this is the XAML code:

 <UserControl x:Class="BezierCurveSample.View.LandmarkControl"
             xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
             xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
             xmlns:mc="http://schemas.openxmlformats.org/markup-compatibility/2006" 
             xmlns:d="http://schemas.microsoft.com/expression/blend/2008" 
             mc:Ignorable="d" 
             x:Name="UserControl"
             d:DesignHeight="300" d:DesignWidth="300">
    <Path x:Name="path" Stroke="{Binding PathColor, 
                        ElementName=UserControl}" StrokeThickness="1"/>
</UserControl>  

Examples of Usage

Using the control for creating the data template for the LandMarkViewModel:

<DataTemplate DataType="{x:Type ViewModel:LandmarkViewModel}">
   <PointInterpolation.View:LandmarkControl x:Name="control"
   Points="{Binding LandmarkPoints}" Visibility="{Binding IsVisible,
   Converter={StaticResource BoolToVisibilityConverter}}" ToolTip="{Binding Label}"/>
   <DataTemplate.Triggers>
       <DataTrigger Binding="{Binding IsSelected}" Value="True">
           <Setter Property="PathColor" TargetName="control" Value="Red"/>
       </DataTrigger>
   </DataTemplate.Triggers>
</DataTemplate>

Now everywhere a LandMarkViewModel is displayed, this data template will show the item as a LandMarkControl. It needs to be rendered on a Canvas:

 <ListBox x:Name="landMarks" ItemsSource="{Binding Landmarks}">
    <ListBox.Template>
    <ControlTemplate>
        <Canvas IsItemsHost="True"/>
    </ControlTemplate>
    </ListBox.Template>
</ListBox> 

This is a final image example:

References

• Bézier curve
• De Casteljau's algorithm
• Interpolation By Bezier Curves

History

• 6^th May 2014: Initial version
• 4^th July 2023: Update the links and references. Added references to the original article, and also to some other implementations.