Introduction
The purpose of this post is to present a possible animation of Quicksort algorithm using JavaScript.
Quicksort is a practical and fast sorting algorithm. It is a fundamental topic
in the standard algorithm course in computer science.
The algorithm for Quicksort serves as a good example of the divide-and-conquer algorithm-design technique; a technique for which the resulting algorithm can be compactly and elegantly expressed using recursion.
As an aid to understanding the algorithm, an educator might show a trace of the algorithm's execution on some specific input.
The trace normally shows the content of the input array and other key parameters at various stages during execution. This is essentially what our JavaScript code does but in a vivid way.
The animated Quicksort algorithm can be run from here.
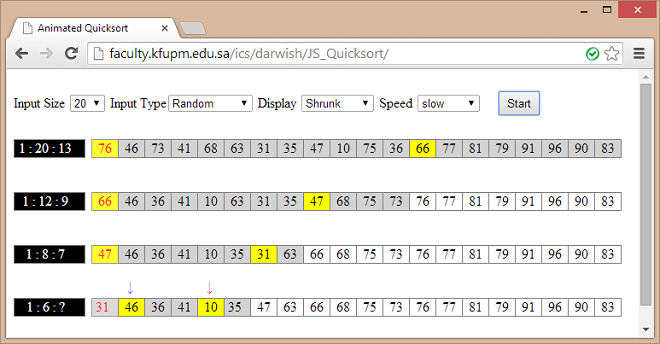
The interface provides one of two views (Display list-box). In the "Shrunk" view, the array is shown for every call of the algorithm with the values for the lo,hi, and mid parameters shown to the left. The line-display for the current
array dynamically changes with every swap.
In the "Expanded" view, the array is shown on a separate line for every swap of elements with the swapped elements highlighted using a distinct color. In both views, the elements from lo to hi are shown with a gray background, while other elements will have a white background. The pivot is identified with red foreground color.
The approach used for animation uses the same technique presented by the author in the
Tower-of-Hanoi article.
As noted by the author, placing the setInterval() calls directly within the procedure to be animated is a recipe for chaos. An effective alternative is to run the normal
unanimated procedure until completion whilst using a stack to save the parameters of interest.
Then process the stack and utilize JavaScript setInterval() function
combined with some visual elements to show the algorithm progress.
How does Quicksort work?
The recursive algorithm for Quicksort can be expressed by the following Quicksort(A, lo, hi) JavaScript function:
function Quicksort(A, lo, hi)
{ if (lo < hi)
{ var mid = Partition(A,lo,hi);
Quicksort(A,lo,mid-1);
Quicksort(A,mid+1,hi);
}
}
The input to the function is an array A of the items to be sorted.
The lo and hi parameters denote, respectively, the lowest index
and highest index of some unsorted section within the array.
For the initial call of the above function, the lo and hi parameters are respectively set (by caller) to the first (leftmost) and last (rightmost) indices of the array.

As illustrated by the preceding figure, Quicksort uses a divide-and-conquer strategy, dividing
the input array into two parts (sections) and sorting each part recursively.
Quicksort uses an auxiliary procedure to perform in-place partitioning of its input (in-place means without using an additional working array). The Partition procedure works as follow:
it picks an element P and arranges the elements so that elements ≤ P are moved to the left side of the sequence and the elements > P are moved to the right side.
The element P used for partitioning is referred to as the pivot element.
The pivot can be any of the elements in the input sequence to be partitioned;
however, quite often, the first (leftmost) element is chosen as the pivot.
function Partition(A, lo, hi)
{
paramStack.push([-lo,hi]);
var pivot = A[lo];
var left = lo+1;
var right = hi;
while (left <= right)
{ while ((left <= right) && (A[left] <= pivot)) left++;
while ((left <= right) && (A[right] > pivot)) right--;
if (left < right)
{
paramStack.push([left,right]);
var t = A[left]; A[left] = A[right]; A[right] = t; left++; right--;
}
}
A[lo] = A[right]; A[right] = pivot;
paramStack.push([lo,right]);
return right;
}
One simple algorithm for partitioning the input array is given by the preceding Partition() function.
Note: The function includes modifications in three places (the lines in bold) that use paramStack.push() to save the lo and hi values as well as the locations of the array elements being swapped.
This uses two pointers (left and right) that are, respectively, set to the start and end of the array to be partitioned.
The left pointer moves toward the right, skipping elements ≤ pivot,
whereas the right pointer moves toward the left, skipping elements > pivot,
but where the left and right pointers stop and left < right, the corresponding elements are swapped.
The process ends when the left and right pointers meet or pass each other.
Then a final swap involving the pivot element and the element pointed to by
the right pointer is executed to put the pivot into its proper sorted location.
Animation of Quicksort

As shown by the preceding figure, our program code for the animated Quicksort consists of six functions:
ExecuteQS(), Quicksort(), Partition(), ProcessStack(),
PrintArray(), AnimateArrow().
The above figure shows the relationship among these functions.
The functions Quicksort() and Partition() are as given previuosly.
The following shows partial code for the other functions.
var A;
var paramStack;
function ExecuteQS()
{
paramStack=[];
var B = A.slice();
Quicksort(A,1,A.length-1);
A = B.slice();
ProcessStack();
}
function ProcessStack()
{ var elem = document.getElementById("arr0");
if (elem) elem.parentNode.removeChild(elem);
elem = document.getElementById("arr1");
if (elem) elem.parentNode.removeChild(elem);
if (paramStack.length==0)
{ PrintArray(A,-1,0); return; }
gelem1 = null; gelem2 = null;
newRow = false;
var param = paramStack.shift();
left = param[0]; right = param[1];
if (left < 0)
{ newRow =true;
lo = -left; hi = right;
prevleft = lo;
prevright = hi;
param = paramStack.shift();
left = param[0]; right = param[1];
}
dispLeft = left-prevleft;
dispRight = prevright-right ;
if (left==lo) dispLeft = right - prevleft;
PrintArray(A, prevleft, prevright);
prevright = right; prevleft = left;
var t = A[left]; A[left] = A[right]; A[right] = t;
if (!Timer1) Timer1 = setInterval(AnimateArrow,Speed);
}
function PrintArray(A, prevleft, prevright)
{
}
function AnimateArrow()
{
}
Concluding Remarks
In the rendered animation, the left arrow is not allowed to move past the
right arrow. This behavior is acceptable, since the data that is saved to the stack are places of swaps and not necessarily all the locations that the left arrow has passed through. The "predefined" example for n=20 shows (first line of output) that the left arrow is not moving because its current location is where the right arrow will end up.
The program code was tested in latest versions of popular browsers. It works
properly in latest versions of IE (version 11), Chrome (version 30), and
Firefox (version 24).
