Introduction
This article is going to explain the basics of evolutionary algorithms with the example of an easy to use Evolution class written for C# and the example of Schwefel's function. You can use this project to find solutions for any system which takes numbers as input arguments and a value in return to maximize the system. Such as efficiency of a wind turbine or value of a function.
Why Do I Need Evolution?
Let's assume you have a black box with 2 sliders with each 10 positions. The output of this black box is energy. You can try to derive an analytical model of the black box or you can use combinatorics to find the maximum energy output. Let's try to imagine that: You have 10^2 Positions to try to find the best solution. What happens if you have 20 sliders with 100 positions? You get 20^100 possibilities. Not all time in the Universe is enough to try all positions. Here evolutions comes into play. It will not try all possibilities but it will always find good slider positions in a relatively short amount of time.
Reality is much more complicated than this. Imagine you build an engine. You have 4000 free parameters such as material compositions and widths of parts. You want to maximize the engine for efficiency. Evolution .NET only needs a reference to the free parameters and the efficiency in return. The only requirement is that you can calculate the efficiency somewhere else and feed it back to the class.
If you want to try it for yourself, feel free to download the demo project.
Using the Code
This class was made to be as intuitive as possible. You only need to say: Here are my variable references, please give me a good solution for my problem. No wrapper classes needed. Very handy. All the magic stuff happens behind the scenes.
double a=0;
var Evo=new Evolution(EvolutionMode.Maximize);
Evo.AddVariable(ref a);
while(true)
{
Evo.Fitness=Math.Sin(a/2);
}
Many things are happening here:
- You tell the Evolutionary algorithm to maximize fitness. If you would Minimize the loop fitness value would approach
-1. - The class does not know how the fitness value is calculated, but it will find the right solution.
- "
a" is changed in the moment the Fitness property is set. There is an internal reference list of IntPtr - You alternate in the standard range for evolution of -500 , 500
Notice: The value of "a" is changed after you have passed it to a function without extra code.
The value of "a" will approach p. A test run showed Fitness to be 0.9999999999946 which is a good approximation for the high point of this function (1).
This class doesn't only support double types but almost all signed numeric types. Float, Int, Double, even Bool. And all lists and public properties of these types.
Behind the Scenes
This class is a self adapting genetic algorithm which means that evolutionrate and other parameters can be changed by the user and are also changed by the class itself.
An evolutionary algorithm uses a hidden list of numbers called the genome. A genome has a value assigned called the fitness. Goal of the evolutionary algorithm is to maximize the fitness value. As discussed in the second paragraph, trying all possibilities is not an option. An evolutionary algorithm uses three principles.
- Reproduction
- Mutation
- Selection
In fact, these are the three things happening in nature all the time. The fourth step is implied and also very important: Repeat as long as you are not happy with the outcome.
For a good introduction about the main ideas, please check out:
In the background, there is a sorted list of genomes and fitness values. This list is called population. Its size can be changed and is 100 at stock. Below, you see the lines responsible for finding better values than before.
if (SafeRandom.Percent(20) && Population.Count > 2)
{ genome = neu.Marry(Population[Population.Count - 2]).genome; return; }
if (SafeRandom.Percent(80)){genome=neu.Mutate(Properties.Mutationrate,Properties).genome;return;}
if (SafeRandom.Percent(20) && Population.Count > 2)
{ genome = neu.Marry(Population[(int)SafeRandom.Between(0,Population.Count-2)]).genome; return; }
genome=neu.Mutate(100,Properties).genome;
There is no proven optimal percentage of the percent values. These are empirical values and optimize the time needed to encounter one optimum.
There are 3 outcomes here:
- crossover
- mutation
- random
Crossover is replacing a genome with another good genome from a certain (random) startindex. This is not necessary as mutation can do something similar, but it really improves the time needed to find the perfect configuration. Mutation varies some of the genes with a certain probability. This is good if you already are in a local maximum and still try to get a better score. And random is important to find other maxima which could turn out to be better.

The lines below are responsible for self adaptation. Each mutation sequence varies the genome between a min and a max. It is a random process and thus a normal distributed process. In this case, Tau (the max genome change in one generation) is defined to be the number of steps it would take minimum to get from the global maximum to the global minimum. You can see that the accuracy is proportional to the search space. If no better solution is found 10x the Tau value is decreased. If the value is at 1/300th of the global search space the algorithm recognizes a local minimum and calls the OptimumReached event.
if (noimprove > 10 && Properties.Selfadapting == true&&Properties.Tausteps<300)
{
Properties.Tausteps++;
noimprove = 0;
}
if (noimprove>15&&Properties.Tausteps>=300)
{
bool cont=false;
if (OptimumReached != null)
{
var arg = new EvolutionEventArgs(gen, DateTime.Now - start.Value);
OptimumReached(this, arg, ref cont);
if (arg.Hardreset == true) { Population.Clear();
genome = genome.Select(x => x = 0).ToList(); this.StartTraining(); }
Continue = cont;
}
}
There is no possible way to know if you actually found the global optimum, there could always be a better solution in your search space.
Sample Project
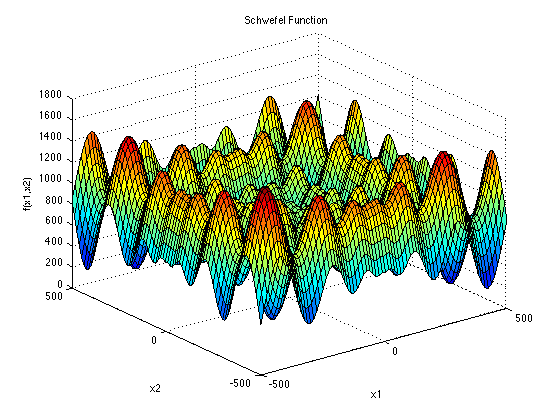
This sample project uses the evolution class to find the minimum point of Schwefel's function.
f(x,y) = (-x * Math.Sin(Math.Sqrt(Math.Abs(x)))) + (-y * Math.Sin(Math.Sqrt(Math.Abs(y))))
using Evolution;
static void Main(string[] args)
{
double x = 0;
double y = 0;
var evolute = new Evolution(EvolutionMode.Minimize);
evolute.AddVariable(ref x);
evolute.AddVariable(ref y);
evolute.OptimumReached += evolute_OptimumReached;
evolute.Properties.Globalmin = -500;
evolute.Properties.Globalmax = 500;
while (evolute.Continue)
{
evolute.Fitness = (-x * Math.Sin(Math.Sqrt(Math.Abs(x)))) + (-y * Math.Sin(Math.Sqrt(Math.Abs(y))));
Console.WriteLine(" x:"+x+" y:"+y+" = " +evolute.Fitness);
}
Console.Clear();
Console.WriteLine("Schwefel’s Function has its minimum at:");
double val = (-x * Math.Sin(Math.Sqrt(Math.Abs(x)))) + (-y * Math.Sin(Math.Sqrt(Math.Abs(y))));
Console.WriteLine(" x:" + x.ToString("0.000") +
" y:" + y.ToString("0.000") + " Z= " + val);
Console.ReadKey();
}
static void evolute_OptimumReached(Evolution Evo, EvolutionEventArgs Arg, ref bool Continue)
{
Continue = false;
Console.WriteLine("Found minimum after: " + Arg.Duration);
}
Please notice: The OptimumReachedEvent which is very handy in the while loop. As a user, you probably don't know when to stop a function. This event gets fired if there is no significant change in fitness over the past couple generations. The event allows you to stop, continue or start completely from new if you are unhappy with the fitness and gives you some other statistical values as arguments.
The function has a minimum value of -837.9658 at x = y = 420.9687
The sample project has an output of -837.965773 at x=420.968 and y = 420,972
Some mechanism were not described for simplicity. Please feel free to download the source (VS2013).
Conclusion
Evolution .NET is a lightweight implementation of an evolutionary algorithm. It does not differentiate between lists properties or variables. It has an eventhandler to "know" when to stop the evolutionloop.
This class doesn't need a wrapper class for the problem. Variables lists of variables and properties can be directly added. If you use the redist DLL, you don't need to compile with /unsafe.
Points of Interest
During my coding, I encountered the problem to save a reference to a value type into a list and change it later. Managed code strongly prohibits to store ref arguments. All lists are stored as reference but I wanted to use the same variables in the same scope.
Dead End 1
List<ref int>
Dead End 2
This function looked promising:
static void change(ref int a)
{
var variables = new StackTrace().GetFrame(1).GetMethod().GetMethodBody().LocalVariables;
}
Solution
public void AddVariable(ref double Variable)
{
unsafe
{
fixed (void* location = &Variable)
{
pointers.Add(new IntPtr(location));
pointertypes.Add(Variable.GetType());
}
}
}
This is the final solution for ref variables. Lists and properties of class instances can be stored and changed in fully managed code. There is unfortunately no other way to do this (Atleast, I don't know one yet).
The solution allows blittable types to be passed by ref and changed later. All other types are passed as List which is always passed by reference. So problem solved.
http://msdn.microsoft.com/en-us/library/75dwhxf7%28v=vs.110%29.aspx
