Introduction:
Merge sort is divide and conquer sorting technique where we divide the whole array in to parts then apply merge technique on them and then combine them in order to produce the final sorted array. Merge sort consist of two basic algorithms called MERGE and MERGE_SORT.
Background:
The basic algorithm MERGE is the procedure of combining two sorted arrays into a new sorted array.
It is like say there are two arrays,
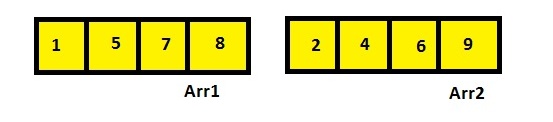
Now we will apply MERGE technique on it.
- Firstly we will create a new array of size m+n where m is the size of the Arr1 and n is the size of the Arr2. Like in this case m=4 and n=4. Hence our new array Arr3 will of size 4+4=8.

- Now we will have two pointers first pointing at the first position of Arr1 and the other on the 1st position of the Arr2.
- Then they go on comparing the values of the two pointers. The pointer with lesser value copy the value to the Arr3 and move a place right.

- Now for the first comparison Arr1[0]=1 and Arr2[0]=2. So as 1<2 hence Arr3[0]=1 and the pointer at Arr1[0] incements and now points towards Arr1[1].

- Similarly now Arr1[1]=5 and Arr2[0]=2. We know that 2<5 and hence Arr3[1]=Arr2[0]=2. Pointer pointing towards Arr2[0] increments and now pointing towards Arr2[1].

- Similarly now Arr1[1]=5 and Arr2[1]=4. We know that 4<5 and hence Arr3[2]=Arr2[1]=4. Pointer pointing towards Arr2[1] increments and now pointing towards Arr2[2].

- Similarly after several steps we get,

It actually compares the elements of both the array and choose the small one and add it in the new array.
In this manner the both arrays are combined into a new sorted array.
The algorithm of MERGE is,
MERGE ( A, low1, high1, low2, high2 )
- while low1<=high1 and low2<=high2 then
- if A[low1] > A[low2] then B[i++] = A[low2++]
- else if A[low1] < a[low2] then B[i++] = A[low1++]
- else
- B[i++] = A[low1++]
- B[i++] = A[low2++]
- End while
- while low1 <= high1
- B[i++] = A[low1++]
- End while
- while low2 <= high2
- B[i++] = A[low2++];
- End while
- for j = low upto j<i
- A[low++] = B[j]
- Increment j by 1
- End MERGE
Then comes the merge sort algorithm. It actually divide the given array to minimum size and then go on combining the arrays by MERGE to sorted new list.
MERGE_SORT( A, low, high )
- if low < high then
- mid = ( low+high )/2
- MERGE_SORT( A, low, mid )
- MERGE_SORT( A, mid+1, high )-
- MERGE( A, low, mid, mid+1, high )
- END MERGE_SORT
Example,

The working diagram of the sorting is

Now consider a MERGE_SORT(A,1,6). Means a Merge sort of an array of 6 elements indexed from 1 to 6.
Th flow of control in this recursive algorithm is,
In case of Time Complexity,
In MERGE() algo we copy n (say) elements of array 1 to array 3 and m (say) elements of array 2 to array 3
So the complexity is O(n+m) which can be said as O(n)
So the complexity of Merging two sorted arrays is O(n)
MERGE_SORT( A, low, high )----------------------------------->T(n)
- if low < high then
- mid = ( low+high )/2
- MERGE_SORT( A, low, mid )----------------------->T(n/2)
- MERGE_SORT( A, mid+1, high )------------------->T(n/2)
- MERGE( A, low, mid, mid+1, high )---------------->O(n)
So the equation is T(n)=2*T(n/2)+O(n)
Using Master's theorem, ( Check it by http://en.wikipedia.org/wiki/Master_theorem )
T(n)=O(nlogn)
Code:
It is one of the standard form of merge_sort using C
#include<stdio.h>
void merge(int arr1[],int ll1,int ul1,int ll2,int ul2)
{
int i=0,k,ll=ll1;
int arr3[100];
while(ll1<=ul1&&ll2<=ul2)
{
if(arr1[ll1]<arr1[ll2])
arr3[i++]=arr1[ll1++];
else
arr3[i++]=arr1[ll2++];
}
while(ll1<=ul1)
arr3[i++]=arr1[ll1++];
while(ll2<=ul2)
arr3[i++]=arr1[ll2++];
for(k=0;k<i;k++)
arr1[ll++]=arr3[k];
}
void merge_sort(int arr1[],int ll,int ul)
{
int mid;
if(ll<ul)
{
mid=(ul+ll)/2;
merge_sort(arr1,ll,mid);
merge_sort(arr1,mid+1,ul);
merge(arr1,ll,mid,mid+1,ul);
}
}
void main()
{
int arr1[100];
int n,i;
printf("\nEnter the no. of elements present in the array :");
scanf("%d",&n);
for(i=0;i<n;i++)
{
printf("\narr[%d]=",i);
scanf("%d",&arr1[i]);
}
merge_sort(arr1,0,n-1);
printf("\nThe sorted array is...");
for(i=0;i<n;i++)
{
printf("\narr[%d]=%d",i,arr1[i]);
}
}
Conclusion:
This is the standard description of merge sort. It is a divide and conquer method of sorting. Merge sort is a sorting where best,worst and average case time complexities are the same.
Reference:
- Introduction to Algorithms by CORMEN, LEISERSON, RIVEST, STEIN
- www.wikipedia.org ( the moving picture and the url is taken from wikipedia )
