MultiClass Logistic Classifier in Python

Introduction

In this article, we look at the basics of MultiClass Logistic Regression Classifier and its implementation in Python.

Background

• Logistic regression is a discriminative probabilistic statistical classification model that can be used to predict the probability of occurrence of a event.
• It is a supervised learning algorithm that can be applied to binary or multinomial classification problems where the classes are exhaustive and mutually exclusive.
• Inputs to classification algorithm are real valued vectors of fixed dimensionality and outputs are the probability that input vector belongs to the specified class.
• Logistic Regression is a type of regression that predicts the probability of occurrence of an event by fitting data to a logistic function .
• Logistic Regression can also be considered as a linear model for classification.
• Logistic function is defined as:

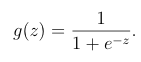
The domain of logistic function lies between [0,1] for any value of input z.

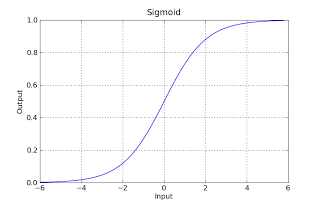
Thus, it can be used to characterize a cumulative distribution function.

The function to apply logistic function to any real valued input vector "X" is defined in Python as:

# function applies logistic function to a real valued input vector x
def sigmoid(X):
   # Compute the sigmoid function
   den = 1.0 + e ** (-1.0 * X)
   d = 1.0 / den
   return d

• The Logistic Regression Classifier is parametrized by a weight matrix and a bias vector \(\mathcal{W},\mathcal{b}\)
• Classification is done by projecting data points onto a set of hyper-planes, the distance to which is used to determine a class membership probability.
• Mathematically, this can be expressed as \( \begin{eqnarray*} P(Y=i|x, W,b) =\frac {e^{W_i x + b_i}}{\sum_j e^{W_j x + b_j}} \\ \end{eqnarray*}\)
• Corresponding to each class \(y_i\)logistic classifier is characterized by a set of parameters \(W_i,b_i\).

The above function is also called as softmax function. The logistic function applies to binary classification problem while the softmax function applies to multi-class classification problems.

# softmax function for multi class logistic regression
def softmax(W,b,x):
   vec=numpy.dot(x,W.T);
   vec=numpy.add(vec,b);
   vec1=numpy.exp(vec);
   res=vec1.T/numpy.sum(vec1,axis=1);
   return res.T;

The parameters (W,b) are the weight vector and bias vector respectively. Let N be the dimension of input vector and M be the number of classes.

The dimension of W is \(MxN\) while that of B is (Mx1). The output of the softmax function if a vector of dimension \(Mx1\).

• These parameters are used to compute the class probability.
• Given a unknown vector (x), The prediction is performed as
  $\begin{eqnarray*} y_{pred} = argmax_i P(Y=i|x,W,b) \\ y_{pred} = argmax_i \frac {e^{W_i x + b_i}}{\sum_j e^{W_j x + b_j}} \end{eqnarray*}$
  The code for the prediction function in Python is as follows:

# function predicts the probability of input vector
# the output y is MX1 vector (M is no of classes)
def predict(self,x):
    y=softmax(self.W,self.b,x);
    return y;

The code for classification function in Python is as follows:

# function returns the lables corresponding to the input y
def lable(self,y):
    return self.labels[y];

# function classifies the input vector x into one of output lables
# input is NXD vector then output is NX1 vector

def classify(self,x):
    result=self.predict(x);
    indices=result.argmax(axis=1);
    #converting indices to lables
    lablels=map(self.lable, indices);
    return lablels;

The validation function accepts validation data and predicts the accuracy of model on the data set.

 # validation function to test the accuracy of model

def validate(self,x,y):
    #classify the input vector x
    result=self.classify(x);
    y_test=y
    #computer the prediction score
    accuracy=met.accuracy_score(y_test,result)
    #compute error in prediction
    accuracy=1.0-accuracy;
    print "Validation error   " + `accuracy`
    return accuracy;

• Given a set of labelled training data \({X_i,Y_i}\)where \(i \text{ in } {1,\ldots,N} \), we need to estimate these parameters.

The essential components of Machine learning framework are:

• Model ( Logistic Regression) - parameterized family of functions
• Loss function - quantitative measurement of performance
• Learning algorithm - Training criteria
• Optimization algorithm - optimization algorithms

Learning Algorithm

• In general, any machine learning algorithm consists of a model, loss function, learning algorithm and optimizer.
• The learning algorithm estimates the parameters of model. This is done using optimization technique by maximizing some objective function. The objective function in case of machine learning algorithms is called as a loss function.
• The optimization techniques work by defining a objective function and then find the parameters of the model that maximizes/minimizes the objective function.

Loss Function

• Ideally, we would like to compute the parameters so that the (0-1) loss is minimized
  $\begin{eqnarray*} \ell_{0,1} = \sum_{i=0}^{|\mathcal{D}|} I_{f(x^{(i)}) \neq y^{(i)}} \\ f(x)= argmax_k P(Y=y_k |x,\theta) \end{eqnarray*}$
• \(P(Y=y_k |x,\theta)\) is modeled using logistic function.
• The (0-1) loss function is not differentiable, hence optimizing it for large modes is computationally infeasible.
• In the present application, negative log-likelihood is used as the loss function.
• Optimal parameters are learned by minimizing the loss function.

Estimation Technique/Learning Algorithm

• Estimation technique called Maximum Likelihood estimation is used to perform this operation.
• The method estimate's the parameters so that likelihood of training data \(\mathcal{D}\) is maximized under the model parameters
• It is assumed that the data samples are independent, so the probability of the set is the product of probabilities of individual examples.

• It should be noted that Likelihood of correct class is not same as number of right predictions.
• Log Likelihood function can be considered as differential version of the (0-1) loss function.

Optimizer - Graidient Based Methods for Minimization

Let us consider a single data sample for the gradient computation. Let the data sample belong to class \(i\). Corresponding to each output class, we have a output matrix \(W_i\) and bias vector \(b_i\).

We need to compute the gradients for all the elements of \(W_i\) and \(b_i\).

If N be the number of dimensions of input vector and M be the number of output classes.

\(W_i\) will be a MxN vector and \(b_i\) will be Mx1 vector:

• In the present application, gradient based methods are used for minimization.
• The cost function is expressed as
  $\begin{eqnarray*} L(\theta,\mathcal{D}) = - log P(Y=y_i | X=x_i,W,b) \\ L(\theta,\mathcal{D}) = - log \frac {e^{W_i x + b_i}}{\sum_j e^{W_j x + b_j}} \\ L(\theta,\mathcal{D}) = - log {e^{W_i x + b_i}}- log {\sum_j e^{W_j x + b_j}} \\ L(\theta,\mathcal{D}) = - {W_i x + b_i} + log \frac{1}{\sum_j e^{W_j x + b_j}} \\ \end{eqnarray*}$
  $\begin{align} \nabla_{\mathbf{w}_i}\ell(\mathbf{w}) &= \frac{\partial}{\partial \mathbf{w}_i}\left(\mathbf{w}_{i}^T\mathbf{x} - \log\left( \sum_{k'}^K \exp(\mathbf{w}_k^T\mathbf{x}) \right) \right) \\ =& \left(\frac{\partial}{\partial \mathbf{w}_i}\mathbf{w}_i^T\mathbf{x} - \frac{\partial}{\partial \mathbf{w}_i}\log\left( \sum_{k'}^K \exp(\mathbf{w}_i^T\mathbf{x}) \right) \right) \\ =& \left(\mathbf{x_i} - \frac{\mathbf{x_i}\exp(\mathbf{w}_i^T\mathbf{x})}{\sum_{k'}^K \exp(\mathbf{w}_i^T\mathbf{x})} \right) \end{align}$
  For the all other \(W_j\) for which \(j \ne i\)
  $\begin{align} \nabla_{\mathbf{w}_j}\ell(\mathbf{w}) =& \frac{\partial}{\partial \mathbf{w}_j}\left(\mathbf{w}_{i}^T\mathbf{x}_i - \log\left( \sum_{k'}^K \exp(\mathbf{w}_k^T\mathbf{x}) \right) \right) \\ =& \left(\frac{\partial}{\partial \mathbf{w}_j}\mathbf{w}_i^T\mathbf{x} - \frac{\partial}{\partial \mathbf{w}_j}\log\left( \sum_{k'}^K \exp(\mathbf{w}_i^T\mathbf{x}) \right) \right) \\ =& \left( - \frac{\mathbf{x}_j\exp(\mathbf{w}_j^T\mathbf{x})}{\sum_{k'}^K \exp(\mathbf{w}_k^T\mathbf{x})} \right) \end{align}$
• This can be computed in Python as:
  Python

  # function computes the negative log likelihood over input dataset
  #  params is optional argument to pass parameter to classifier
  #  Useful in cases of iterative optimization routines for function evaluations
  # like scipy.optimization package
  def negative_log_likelihood(self,params):
      # args contains the training data
      x,y=self.args;
  
      self.update_params(params);
      sigmoid_activation = pyvision.softmax(self.W,self.b,x);
      index=[range(0,np.shape(sigmoid_activation)[0]),y];
      p=sigmoid_activation[index]
      l=-np.mean(np.log(p));
      return l;
  

• The first part of the sum is affine, second is a log of sum of exponential's which is convex. Thus, the loss function is convex and therefore has a unique global maxima/minima.

• Thus, we compute the derivatives of the loss function \(L(\theta,\mathcal{D}) \text{with respect to} \theta ,\partial{\ell}/\partial{W} \text{ and } \partial{\ell}/\partial{b}\)

• Different gradient based minimization exist like gradient descent, stochastic gradient descent, conjugate gradient descent, etc.

The Python code for computing gradients are:

# function to compute the gradient of parameters for a single data sample
def compute_gradients(self,out,y,x):
    out=(np.reshape(out,(np.shape(out)[0],1)));
    out[y]=out[y]-1;
    W=out*x.T;
    res=np.vstack((W.T,out.flatten()))
    return res;

# function to compute the gradient of loss function over all input samples
#    params is optional input parameter passed to the classifier, which is
#   useful in cases  of iterative optimization routines,added for compatiblity with
#    scipi.optimization package
def gradients(self,params=None):
    # args contains the training data
    x,y=self.args;
    self.update_params(params);
    sigmoid_activation = pyvision.softmax(self.W,self.b,x);
    e = [ self.compute_gradients(a,c,b) for a, c,b in izip(sigmoid_activation,y,x)]
    mean1=np.mean(e,axis=0);
    mean1=mean1.T.flatten();
    return mean1;

The aim of gradient descent algorithms would be to take a small step along the direction of gradient to reach to global maxima.

Thus gradient descent algorithms are characterized by the update and evaluate steps. At each iteration, the values of parameters are updated, i.e. (W,b) and then logistic loss function is evaluated wrt training data set. This process is repeated till we are certain that obtained set of parameters result in a global maximum values for negative log likelihood function.

Optimizer

We also do not use custom implementation of gradient descent algorithms rather the class implements optimizer using the newtons conjugate gradient method fmin_cg from the Scipy optimization package. The input to the optimizer are the evaluation function, initial parameters and partial derivatives and output is the optimized parameters that maximuze the input functions.

Callback functions are also specified which perform validation tests to computer the accuracy on the training database.

To use the scipy optimization package, we require the input to the functions to be the parameter values that need to be optimized. The functions evaluated at the optimized values are loss function, gradient or Hessian of loss functions. The output of optimization process are the optimized parameter values. The output of derivative function are the partial derivatives wrt the function evaluated at values specified by the input parameter value.

We define a class called Optimizer that performs optimization. It currently supports conjugate gradient descent and stochastic gradient descent algorithms.

In the present article, we will look at using the conjugate gradient descent algorithm.

The optimization function found in optimizer.py file corresponding to conjugate gradient descent algorithm is as below:

self.iter=0;
index=self.iter;
batch_size=self.batch_size;  
            
# training data
x=self.training[0];
y=self.training[1];
            
# training data batch for each iteration
train_input=x[index * batch_size:(index + 1) * batch_size];
train_output=y[index * batch_size:(index + 1) * batch_size];
train_output=np.array(train_output,dtype=int);            

self.args=(train_input,train_output);            
args=self.args;
# setting the training data in LogisticRegression class
self.setdata(args);
# getting initial parameter from LogisticRegression class
self.params=self.init();

print "**************************************"
print "starting with the optimization process"
print "**************************************"
print "Executing nonlinear conjugate gradient descent optimization routines ...."
res=optimize.fmin_cg(self.cost,self.params,fprime=self.gradient,maxiter=self.maxiter,callback=self.local_callback);
print "**************************************"
print "completed with the optimization process"

self.cost corresponds to the negative_log_likelihood method of LogisticRegression class

self.gradient corresponds to the gradients method of the LogisticRegression class

self.callback method corresponds to callback method in the Logisitic regression class, which is called at each iteration to update parameter values, computer Likelihood and observe other statictics indicating how the optimization is proceeding.

In case of the scipy.optimization package, it computes the cost function and gradient values by passing parameter values to these functions,and performs parameter update based on the result returned by function and gradient evaluations. The parameter values are updated in the LogisticRegression whenever cost or gradient function are called. The parameter values are also updated in each callback iteration loop.

# the function performs training for logistic regression classifier """        
def train(self,train,test,validate):
    if self.n_dimensions==0:
        self.labels=np.unique(train[1]);            
        n_classes = len(self.labels) 
        n_dimensions=np.shape(x)[1];
        self.initialize_parameters(n_dimensions,n_classes);
    # create the optimizer class """       
    opti=Optimizer.Optimizer(10,"CGD",1,600);    
    # set the training and validation datasets"""
    opti.set_datasets(train,test,validate);
    # pass the cost,gradient and callback functions"""
    opti.set_functions(self.negative_log_likelihood,self.set_training_data,
         self.classify,self.gradients,self.get_params,self.callback);
    # run the optimizer"""
    opti.run();

A class called LogisticRegression is defined which encapsulates the methods that are used to perform training and testing of multi-class Logistic Regression classifier.

TRAINING DATASET

• For demonstration, we will use MNIST dataset. The MNIST dataset consists of handwritten digit images and it is divided in 60,000 examples for the training set and 10,000 examples for testing. The official training set of 60,000 is divided into an actual training set of 50,000 examples and 10,000 validation examples All digit images have been size-normalized and centered in a fixed size image of 28 x 28 pixels. In the original dataset, each pixel of the image is represented by a value between 0 and 255, where 0 is black, 255 is white and anything in between is a different shade of grey.
• The dataset can be found at http://deeplearning.net/data/mnist/mnist.pkl.gz.
• The dataset is pickled can be loaded using Python pickle package.
• The data set consists of training, validation and test set.
• The data set consists of feature vector of length 28 x 28 = 784 and number of classes are 10.

#  MAIN FUNCTION 
if __name__ == "__main__":    


     model_name1="/home/pi19404/Documents/mnist.pkl.gz"
     data=LoadDataSets.LoadDataSets();
     [train,test,validate]=data.load_pickle_data(model_name1);
     
     x=train[0].get_value(borrow=True);
     y=train[1].eval();     
     train=[x,y];

     x=test[0].get_value(borrow=True);
     y=test[1].eval();
     test=[x,y];
     
     x=validate[0].get_value(borrow=True);
     y=validate[1].eval();
     validate=[x,y];
     
     classifier=LogisticRegression(0,0);
     classifier.Regularization=0;
     classifier.train(train,test,validate);

Code for saving/loading the model files, passing parameters to optimization functions have not been implemented, these will be added in the future. The output of the training process is shown below. The conjugate gradient optimizer without regularization gives accuracy of 80% with 5 iterations:

... loading data  /home/pi19404/Documents/mnist.pkl.gz
number of dimensions :  784
number of classes  : 10
number of training samples : 50000
iteration   :  0
Loss function   :  1.98470824149
Validation error   0.39827999999999997
iteration   :  1
Loss function   :  1.35257458245
Validation error   0.32438
iteration   :  2
Loss function   :  1.0896595289
Validation error   0.27329999999999999
iteration   :  3
Loss function   :  0.928568922396
Validation error   0.23626000000000003
iteration   :  4
Loss function   :  0.811558448986
Validation error   0.20977999999999997
Warning: Maximum number of iterations has been exceeded
         Current function value: 0.811558
         Iterations: 5
         Function evaluations: 171
         Gradient evaluations: 171
(50000, 784) (50000,)

Code

• Download source code - 3.5 KB
• Alternate link

The code can also be found at Github code repository.

• The Python code for Logistic Regression Classifier can be found at github repository https://github.com/pi19404/OpenVision/tree/master/ImgML/PyVision/LogisticRegression.py file.
• The LoadDataSets.py contains methods to load datasets from pickel files, LogisticRegression.py is the main file that implements the multiclass Logsitic Regression Classifier, while Optimizer.py contains the methods for handling optimization process.
• You may need to install Python packages numpy, scipy
• You may need to install scikit machine learning package. The sklearn.metrics is used for accuracy metrics computation in validation methods of the LogisticRegression class.