This article presents simple software for solving quadratic optimal control problem for linear and nonlinear dynamic systems.
Table of Contents
Introduction
In this article, I'd like to present a compact and simple-to-use software tool for optimal control of dynamic systems. Optimal control is a very broad topic. Its foundation was laid with works by Norbert Wiener, John Ragazzini, Lotfi Zadeh, Richard Bellman, Lev Pontryagin, Rudolf Kalman, and many others in the 1940s - 60s. Optimal control has numerous practical applications. Here, we will focus on the following classic optimal control problem. Our goal is to transfer a given dynamic system from its initial state to some final state with external control inputs. We desire that during this transition system, parameters follow their prescribed trajectories as close as possible. This is a very fundamental task of optimal control with a lot of practical applications. For example, to start of electrical motor limiting initial jump of electric current to acceptable value; promptly damping undesirable oscillations in electronic and mechanical systems, and countless sophisticated applications ranging from spacecraft control to missiles interception.
Dealing with this problem and even its statement requires a lot of math. I will confine myself to the necessary minimum required to describe the problem and understand how to use the software. Some additional recursive formulas are given in an appendix without proof.
Problem Statement
Let's formalize our problem. A dynamic system is described with the following set of differential equations:
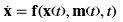 | (1) |
where t is time, x is the state vector consisting of parameters characterizing system behavior, ẋ is vector of the first derivative of x by time, m is the control vector. Normally, the dimension of the control vector does not exceed the dimension of the state vector. In this statement, vector m is independent on vector x, and may be considered as control of the open-loop system. The open-loop control system with input control vector m and state vector x is depicted below:
 |
| Open-Loop Control System |
We’d like to obtain control policy m(t) during the time interval between 0 and the final time of tf which minimizes the cost function:
 | (2) |
where superscript T denotes transposing of vector or matrix, r is the desirable state vector, u is the desirable control vector, Q and Z are weight matrices for the deviation between desirable and actual parameters of state and control vectors respectively. In most cases, Q and Z are diagonal matrices (but not necessarily!). Each diagonal element of them defines the relative weight of the square of the difference between desirable and real values of a parameter at a given moment of time. The matrices may be time-dependent, e.g., it is common practice to increase the relative weight of the differences at the final time to ensure a desirable final state. The problem formulated here is often referred to as a "tracking problem."
Linear Dynamic Systems
Before we come to a solution, let's discuss a special case of dynamic systems. The most well-studied class of the systems is linear dynamic systems, i.e., systems in which dynamics is described with a set of linear differential equations. For such a system, equation (1) may be rewritten as follows:
 | (3) |
where A(t) and B(t) are matrices. First, we will provide a solution for this kind of system, and then spread it to nonlinear dynamic systems.
Discrete Time
Since we are going to offer a numeric solution, we will deal with the system in discrete moments of time. So we will reformulate our problem for discrete time t = k ⋅ Δt, where Δt constitutes a small time interval (sampling interval) and k is a given time step, 0 <= k < N, tf = (N-1) ⋅ Δt. Now equations (1) may be rewritten for discrete time:
 | (4) |
and the linear system is defined as:
 | (5) |
where Fk and Hk are matrices obtained from A(t) and B(t) as follows:
Fk = exp(A(k⋅Δt)⋅Δt) ≅ I+A(k⋅Δt)⋅Δt, Hk = A-1[exp(A(k⋅ Δt)⋅Δt) - I]B ≅ B(k⋅Δt)⋅Δt, where I is unit matrix.
Cost function (2) in discrete time will be reshaped to:
 | (6) |
Solution for the Linear Case
A numeric solution to the problem may be obtained based on Bellman's principle of optimality. Results are quite bulky and presented in the appendix. For general understanding, it is essential to know that mk control policy is calculated in two major runs. First, an inverse calculation run is performed starting with final time step N-1 and going down to initial time 0. The inverse calculation run using system matrices F and H, desirable state r and control u vectors, and weight matrices Q, Z yields some vector ck and matrix Lk. Then the direct run is carried out from time 0 till N-1 obtaining vector mk at each k time step as:
 | (7) |
Both inverse and direct calculation runs are shown in the picture below:
 |
| Calculation scheme |
Vectors cN-k and matrices LN-k are known from the inverse run and dependent on system matrices F and H, user-defined desirable vectors, and weights. They also depend on auxiliary matrices PN-k and vectors vN-k participating in the inverse run and starting from zero initial conditions. On each step of the direct calculation run, we obtain control vector mk based on state vector xk for this time. Then calculate the next state xk+1 using equation (5). This procedure is repeated until the last time moment N-1 giving us both open-loop control policy mk and states of the system xk vs. time. Statement (7) provides us with closed-loop control as depicted below:
 |
| Closed-Loop Control System |
where vector c constitutes closed-loop control and matrix L provides feedback from state vector x. These parameters allow the designer to generate vector m based on the actual state of the system, thus making the system more stable and robust.
Discussion of the Solution for the Linear Case
For linear systems, control policy mk minimum of the cost function (6) is achieved with just one iteration consisting of one inverse and one direct run. As we have stated above, this policy depends on system matrices and user-chosen parameters, namely desirable vectors and weight matrices. These parameters are intuitive enough to reduce the control policy design to a play with them. The user chooses a set of parameters and calculates the control policy and appropriate state trajectories. If she/he is not satisfied with the result, the calculation is repeated for another set of desirable vectors and weight matrices. It is also interesting to observe that if system matrices F, H, and weight matrix Q are time-invariant then feedback matrix L will be also time-invariant, which considerably simplified the design of the system’s controller. For linear case system matrices F, H are normally time-invariant. So, to attain time-invariant feedback, the user should choose constant weight matrix Q, i.e. control without formal strict achievement of desirable final state at the final moment of time. In real life by proper choice of Q, we can achieve a desirable final state in an acceptable time, even before our final time. Although it is convenient to implement control policy using state vector coordinates, in real life usually not all those coordinates are available for measurement. Various techniques have been developed to overcome this difficulty. Different kinds of state coordinate observers may be used to estimate unmeasured coordinates using information for the coordinates available for measurement.
Nonlinear Systems
The nonlinear system case is much more complex. Unlike linear systems, it does not have an overall decision for all kinds of systems. Here, we can try to reduce the nonlinear optimization problem to a linear one using the quasilinearization approach. To use the same math solution, we have to present a general dynamic system description given by equation (1) in a linearized form similar to equation (5). To achieve this, we should consider an iterative calculation process. We can linearize (1) to (5) in a particular point on xk and mk of i-th trajectory:
 | (8) |
where:
 | (9) |
Linearized system matrices F and H are matrices of appropriate partial derivatives of functions f at point k on i-th trajectory. State and control vectors on (i+1)-th trajectory may be presented as:
 | (10) |
Equation (8) may be formulated for increments Δx and Δm. In this case, in cost function (6), new vectors r and u correspond to:
 | (11) |
respectively. This allows us to reduce the nonlinear problem to a sequence of quasilinear iterations, each of which is depicted in the computational scheme figure above. The algorithm consists of the following steps:
- Assuming for iteration i=0 vectors xk and mk (normally all zeros accept xk=0 initial conditions, but the choice is up to the user) calculate linearized all Fki and Hki for i-th trajectory according to (8).
- Calculate new rki and uki for i-th iteration according to (11).
- Calculate Δmki and Δxki using inverse and direct runs as for linear case.
- Calculate xki+1 and mki+1 for (i+1)-th iteration.
- Check condition to stop iterations. This condition may be based, e.g., on the difference between values of cost function compared to the previous iteration, or simply contain a fixed number of iterations. Anyway, if the condition is not satisfied, then steps 1-5 should be repeated until the
stop condition will be satisfied. After the condition was satisfied, policy mk and states xk may be considered as the final solution.
Obtaining exact formulas for partial derivatives of functions f may be tedious work, and becomes impossible when functions f are defined numerically, e.g., as a table. In these cases, it is possible to use simple numeric approximation by giving small increments to a state vector coordinate of partial derivative and computing the result value of f function. The code sample provides appropriate examples.
Method Limitations
Like any numeric approach, this one has its limitations. One limitation is rather obvious and should be considered for both linear and nonlinear cases: the time sampling interval should be small enough to guarantee convergence of calculations. Desirable values of r, u, and weight factors Q and Z should be reasonable to achieve intuitively optimal system behavior. In the case of nonlinear systems, we should clearly understand that this is a "game without strict rules," and thus there is not any guarantee that the technique is applicable to a particular case. The method is sensitive to the computing of linearized system matrices accuracy. More complex methods may be used to estimate the applicability of this approach to a particular nonlinear system, but usage of the try-and-fail approach seems more practical for engineers. Again, in some way dealing with nonlinear systems is still "art rather than science."
Constant Feedback
As in the linear case, control with constant feedback may be considered for nonlinear systems. To obtain constant feedback in nonlinear case weight matrices Q, Z, the initial trajectory for state x and control m should be time-invariant (except for initial state x0), and an acceptable result should be achieved in a single iteration (since system matrices F and H calculated according to (9) depend on previous iteration trajectory). Normally, engineers adopt a rather informal approach to system optimization, when delivering minimum to our cost function is not the ultimate goal but a means to attain acceptable system behavior. So it may be wise in some cases to sacrifice further cost function minimization for the sake of feedback simplicity. It is also possible that in some cases constant feedback may to some extent compensate for nonlinearity. Of course, like everything in nonlinear systems, it is possible not in all cases. An appropriate numeric example will be discussed below.
Usage of Software
.NET
The software is written in plain C# without any additional libraries. In the last update, it has been converted to .NET 6 (DLLs are in .NET Standard 2.0) . .NET demo can be run in Windows and Linux alike by command
dotnet Test.dll
Project MatrixCalc provides arithmetic operations with vectors and matrices including transposition and inversion. The project SequentialQuadratic supports calculations for system optimization and simulation. Project Test uses static methods and interfaces SequentialQuadratic to solve particular problems. DLL SequentialQuadratic has several internal types responsible for different optimization problems (linear with constant weights and desirable values, linear with changed in time weights and desirable values, and appropriate nonlinear). Instances of these types are created with overloaded static methods SQ.Create() and exposed to the caller via a set of appropriate interfaces IBase, IBaseLQExt, ITrackingLQ and INonLinearQ. In order to perform the optimization procedure, the user should call the appropriate method providing input and getting the required interface. Then method RunOptimization() should be called to actually carry out optimization calculations, followed by the method Output2Csv() to write results in comma-separated format to an Excel-compatible *.csv file. To simulate the system with a given control policy, the method Simulate() is called. A sample of the code for optimization of a nonlinear system (Van der Pol oscillator) is shown below:
public static void VanDerPol()
{
const string TITLE = "Van der Pol";
Console.WriteLine($"Begin \"{TITLE}\"");
var lstFormatting = new List<OutputConfig>
{
new OutputConfig { outputType = OutputType.Control, index = 0, title="m0",
scaleFactor=1 },
new OutputConfig { outputType = OutputType.State, index = 0, title="x0" },
new OutputConfig { outputType = OutputType.State, index = 1, title="x1" },
};
const int dimensionX = 2;
const int dimensionM = 1;
const double dt = 0.1;
const int N = 51;
const int maxIterations = 17;
var r = new Vector(dimensionX) { [0] = 0, [1] = 0 };
var u = new Vector(dimensionM) { [0] = 0 };
var Q = new Matrix(dimensionX, dimensionX) { [0, 0] = 1, [1, 1] = 1 };
var Z = new Matrix(dimensionM, dimensionM) { [0, 0] = 1 };
var xInit = new Vector(dimensionX) { [0] = 1, [1] = 0 };
var mu = 1;
var functions = new CalcDelegate[]
{
(k, deltaT, m, x) => x[1],
(k, deltaT, m, x) => mu * (1 - Sq(x[0])) * x[1] - x[0] + m[0]
};
var gradientsA = new CalcDelegate[dimensionX, dimensionX];
gradientsA[0, 0] = (k, deltaT, m, x) => 0;
gradientsA[0, 1] = (k, deltaT, m, x) => 1;
gradientsA[1, 0] = (k, deltaT, m, x) => -(2 * mu * x[0] * x[1] + 1);
gradientsA[1, 1] = (k, deltaT, m, x) => mu * (1 - Sq(x[0]));
var gradientsB = new CalcDelegate[dimensionX, dimensionM];
gradientsB[0, 0] = (k, deltaT, m, x) => 0;
gradientsB[1, 0] = (k, deltaT, m, x) => 1;
(SQ.Create(functions, gradientsA, gradientsB, Q, Z, r, u, xInit, dt, N,
(currCost, prevCost, iteration) => iteration > maxIterations)
.RunOptimization()
.Output2Csv("VanDerPol_ExactGrads", lstFormatting) as INonLinearQ)
.OutputExecutionDetails(isExactGradient: true);
var delta = 0.1;
(SQ.Create(functions, new Vector(dimensionM, delta), new Vector(dimensionX, delta),
Q, Z, r, u, xInit, dt, N,
(currCost, prevCost, iteration) => iteration > maxIterations)
.RunOptimization()
.Output2Csv("VanDerPol_NumGrads", lstFormatting) as INonLinearQ)
.OutputExecutionDetails(isExactGradient: false);
Console.WriteLine($"End \"{TITLE}\"{Environment.NewLine}");
}
Python
I provide a little simplified version of the code written in Python3. Currently, it contains one linear and one nonlinear example. This code runs both in Windows and Linux (I tested it under Ubuntu 20.04) environments. To run the code, you need to install the latest version of Python3 and its numpy and scipy packages, unzip source code, and start file Program.py
in Linux with
python3 Program.py
and in Windows with
python Program.py
command.
Python version supports transients visualization. To activate this feature, please install matplotlib package and remove all comments #1 in file Program.py.
Numeric Examples
Linear System
There is a mechanical system: mass M is moving by force. According to Newton's second law, the force is equal to the result of the multiplication of mass and acceleration which is the second derivative of displacement. Let's denote displacement as x0, velocity as x1, and force as m0. The system is described with the following second-order matrix differential equation:
ẋ = Ax + Bm, where:
| A = | \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}
| , | B = | \begin{bmatrix} 0 \\ 1/M \end{bmatrix}
| , | M = 1 |
| xk=0 = | \begin{bmatrix} 0 \\ 0 \end{bmatrix}
|
Cost function is ∫040[(10 - x0)2 + 3x12]dt
| Q = | \begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix}
| , | Z = | \begin{bmatrix} 0 \end{bmatrix}
| , | r = | \begin{bmatrix} 10 \\ 0 \end{bmatrix}
| , | u = | \begin{bmatrix} 0 \end{bmatrix}
|
Δt = 1, N = 41.
 |
| Transients of the linear system |
| Closed-loop input and feedback factors obtained as a result of calculations are |
| input 4.48, |
| feedbacks: from x0 -0.448 and from x1 -1.22 . |
Van der Pol Oscillator
This is a nonlinear system. Our goal is smooth and fast damping of ongoing oscillations.
ẋ0 = x1
ẋ1 = μ⋅x1⋅(1 - x02) - x0 + m0, μ=1
| xk=0 = | \begin{bmatrix} 1 \\ 0 \end{bmatrix}
|
Cost function is ∫08(x02 + x12 + m02)dt
| Q = | \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}
| , | Z = | \begin{bmatrix} 1 \end{bmatrix}
| , | r = | \begin{bmatrix} 0 \\ 0 \end{bmatrix}
| , | u = | \begin{bmatrix} 0 \end{bmatrix}
|
Δt = 0.1, N = 81.
 |
| Transients of the controlled Van der Pol oscillator after 3 iterations |
In the above case with chosen desirable state and control vectors and weight matrices, we observe good convergent iterative calculations.
Rayleigh Equation with Scalar Control
This is another nonlinear oscillation system. Our goal is the same as in previous case: smooth and fast ongoing oscillations damping.
ẋ0 = x1
ẋ1 = -x0 + (1.4 - 0.14⋅x12)⋅x1 + 4⋅m0
| xk=0 = | \begin{bmatrix} -5 \\ -5 \end{bmatrix}
|
Cost function is ∫05(x02 + m02)dt
| Q = | \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}
| , | Z = | \begin{bmatrix} 1 \end{bmatrix}
| , | r = | \begin{bmatrix} 0 \\ 0 \end{bmatrix}
| , | u = | \begin{bmatrix} 0 \\ \end{bmatrix}
|
Δt = 0.01, N = 501.
 |
| Transients after 3 iterations |
In this case, even the first iteration provides an acceptable result. But the value of the cost function does not steadily reduce for chosen optimization parameters.
Nonlinear System with Constant Feedback
This is a nonlinear system that can be adequately translated from its given initial state to zero state using constant feedback.
ẋ0 = x1
ẋ1 = -x0⋅[π/2 + artan(5⋅x0)] - 5⋅x02 / [2⋅(1 + 25⋅x02)] + 4⋅x1 + 3⋅m0
| xk=0 = | \begin{bmatrix} 3 \\ -2 \end{bmatrix}
|
Cost function is ∫010(5x12 + m02)dt
| Q = | \begin{bmatrix} 0 & 0 \\ 0 & 5 \end{bmatrix}
| , | Z = | \begin{bmatrix} 1 \end{bmatrix}
| , | r = | \begin{bmatrix} 0 \\ 0 \end{bmatrix}
| , | u = | \begin{bmatrix} 0 \\ \end{bmatrix}
|
Δt = 0.01, N = 1001.
 |
| Transients for a single iteration |
 |
| m0 vs. x1 for a single iteration |
The above figures depict transients calculated with our software for chosen weight matrices after a single iteration. The last figure shows relations between controlled state coordinate x1 and control m0 for our calculations.
Two-Link Robotic Manipulator
The application of the described technique to optimal control of a two-link robotic manipulator is presented in this CodeProject post. Implementation may be foumd in the code.
Quadcopter
This CodeProject article
presents optimal control of a quadcopter. The code is a little updated there.
More numeric examples are provided in the code sample.
Conclusions
The article briefly explains the numeric solution of sequential quadratic optimal control problem for linear and nonlinear systems. The quasilinearization approach is used to reduce the nonlinear problem to a set of sequential linear-quadratic problems for a linearized system. Compact and simple-to-use software is provided along with examples of its usage.
Appendix
Parameters c and L in recursive equation (7) for calculation of control vector m in the inverse run may be obtained from dynamic programming Bellman equation (format of this article does not permit to provide appropriate maths transformations) as a set of the following recursive operations:
where P and v are recursively calculated auxiliary matrix and vector respectively, k starts from k = N - 1 with P0 = 0, v0 = 0.
Note that the above calculations require inverting auxiliary W matrix dependent on transfer matrix H, weight matrices, and matrix P.
- 9th January, 2015: Initial version
- 9th June, 2021: Update
- 11th June, 2022: An error fixed in the code
