Introduction
This is sort of an exercise in applied algebra (specifically, application of the equation y = mx + b, the so-called slope-intercept form of a linear equation).
Background
I have a "toy" 3D viewing app written in Python, using Pygame for the UI. It has wireframe display, and a primitive "hidden surface removal" option (namely, sort the polygons by their z coordinates, then "paint" in back-to-front order so the closer polygons hide the further polygons). I wanted to add a hidden-line-removal option, because Pygame doesn't seem to offer an "outlined polygon" drawing method. I thought this code might be a step in that direction. Later, I discovered that MeshLab offers the features I wanted... maybe I'll work on implementing hidden-line-removal someday... maybe...
Using the Code
To use the code, you should install Python (obviously) as well as Pygame (although the intersection algorithm doesn't depend on Pygame, the test app does). Both the 2.x and 3.x flavors of Python should work.
Alternatively, you can just extract four functions (slope(), y_intercept(), intersect() & segment_intersect()) and use them as you see fit.
The function intersect( line1, line2 ) tries to compute the intersection of line1 and line2; it includes a primitive sort of guard against numeric overflow, and returns a point (a tuple (x,y)).
#
# the line 'data structure' looks like this:
line1 = [(100.,100.),(700.,700.)]
# (defines a line segment between the points (100,100) and (700,700))
The line data structure used ensures that line endpoints are compatible with Pygame's line-drawing routines, e.g.:
# draw line1
# ("anti-aliased" and using the color stored in the fgcolor variable,
# which must be defined previously)
pygame.draw.aaline(screen, fgcolor, line1[0], line1[1])
These three functions implement the basic line-intersection-point computation:
def slope(p1, p2) :
return (p2[1] - p1[1]) * 1. / (p2[0] - p1[0])
def y_intercept(slope, p1) :
return p1[1] - 1. * slope * p1[0]
def intersect(line1, line2) :
min_allowed = 1e-5 # guard against overflow
big_value = 1e10 # use instead (if overflow would have occurred)
m1 = slope(line1[0], line1[1])
print( 'm1: %d' % m1 )
b1 = y_intercept(m1, line1[0])
print( 'b1: %d' % b1 )
m2 = slope(line2[0], line2[1])
print( 'm2: %d' % m2 )
b2 = y_intercept(m2, line2[0])
print( 'b2: %d' % b2 )
if abs(m1 - m2) < min_allowed :
x = big_value
else :
x = (b2 - b1) / (m1 - m2)
y = m1 * x + b1
y2 = m2 * x + b2
print( '(x,y,y2) = %d,%d,%d' % (x, y, y2))
return (int(x),int(y))
The function segment_intersect( line1, line2 ) tries to deal with the fact that line1 and line2 define line segments, and there may be no point of intersection between them even when they aren't parallel (i.e., when the intersection point between the infinite lines isn't part of (at least one of) the finite line segments). It returns either the intersection point returned by intersect(), or None (Python's equivalent of Java's null, C's NULL, etc.).
def segment_intersect(line1, line2) :
intersection_pt = intersect(line1, line2)
print( line1[0][0], line1[1][0], line2[0][0], line2[1][0], intersection_pt[0] )
print( line1[0][1], line1[1][1], line2[0][1], line2[1][1], intersection_pt[1] )
if (line1[0][0] < line1[1][0]) :
if intersection_pt[0] < line1[0][0] or intersection_pt[0] > line1[1][0] :
print( 'exit 1' )
return None
else :
if intersection_pt[0] > line1[0][0] or intersection_pt[0] < line1[1][0] :
print( 'exit 2' )
return None
if (line2[0][0] < line2[1][0]) :
if intersection_pt[0] < line2[0][0] or intersection_pt[0] > line2[1][0] :
print( 'exit 3' )
return None
else :
if intersection_pt[0] > line2[0][0] or intersection_pt[0] < line2[1][0] :
print( 'exit 4' )
return None
return intersection_pt
To run the test application:
python linex.py
The test app's UI is very simple. Two line segments are drawn, and their intersection (if any) has a small circle drawn around it. One of the four line segment endpoints is considered the "active" endpoint, indicated by a small red circle. To change which endpoint is "active," press 0,1,2, or 3. To change the location of the "active" endpoint, click in the Pygame window's drawing area with the mouse. To quit, press 'q' (or use one of your OS's shortcuts).
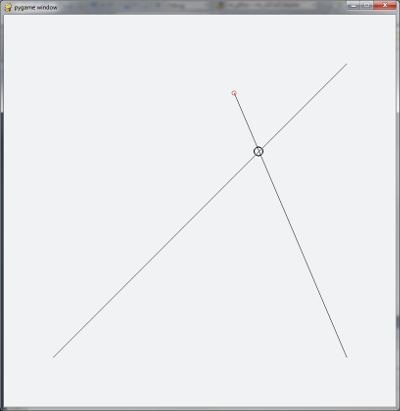
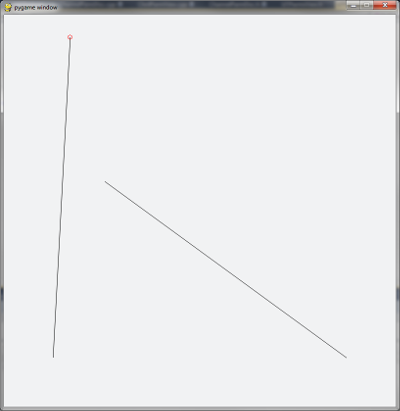
Points of Interest
To guard against numeric overflow, the intersect() function uses a pair of constants to prevent division by zero (or division by any number that might be small enough to cause overflow). Primitive, but it works for this application.
The code is liberally interspersed with print() statements for debugging.
History
- 12 Jan 2015: Version 1 posted
