Using Logistic Regression To Compare Strings

Introduction

link to Download source

Traditional Levenshtein and Jaro-Winkler algorithms not usually give themselves good results because of its limitations, for example, when comparing streets.

Far from using algorithms of some magnitude, if we combine the power of both algorithms we could have a fairly reliable method to compare these chains.

Based on a data set, we will train the machine using logistic regression, taking as inputs the results of applying these algorithms to each pair of strings in the dataset.

Once trained, we have a reliable method to make future comparisons in an automatic way.

Using the code

Setting up the datasource

The first thing we have is the dataset. In my case, the dataset is a comparative streets of different cities where the first and second columns are the streets name to compare and the third represents a value of 0 if there is a significant difference in the street names and a value of 1 elsewhere.

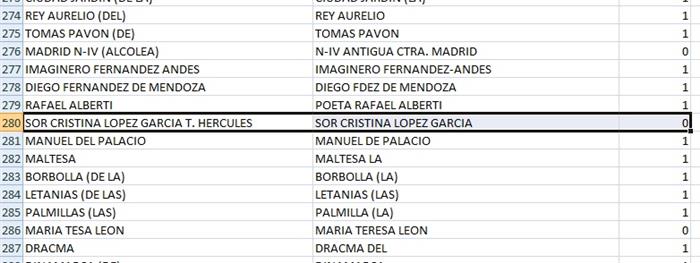
image data source

We will export the excel sheet to a .csv file, using as a field separator the '¦' character. I have choosed this character because there is no street in the dataset that include it. The file has this form:

original data source

Appliying Levenshtein distance and Jaro-Winkler distance algorithms

We will use a class «Elements» to store the datasource and store the result of apliying the distances algorithm.

public class Elements
{
   public string OldName { get; set; }
   public string NewName { get; set; }
   public int IsSame { get; set; } // 1: the streets are the same - 0: the strings are different
   public double Levenshtein { get; set; }
   public double JaroWinkler { get; set; }
}

Now, the code will read all pairs of strings and it will apply the distance algorithms. The result will be written in an output file where the first two columns display the values of the application of both algorithms and the third column displays 1 if the strings can be considered the same or 0 otherwise (just like the third column of the datasource).

string ruta = path + "\\" + filename + ".csv";

List<Elements> lista = new List<Elements>();
StreamReader sr = new StreamReader(ruta);

//Read the datasource and store in la List of Elements
while (!sr.EndOfStream)
{
    string[] data = sr.ReadLine().Split('|');

    lista.Add(new Elements()
    {
        NewName = ManejadorCadena.QuitaAcentos(data[0]).Trim().ToUpper(),
        OldName = ManejadorCadena.QuitaAcentos(data[1]).Trim().ToUpper(),
        IsSame = Convert.ToInt32(data[2])
    });
}
sr.Close();

//Appliying the distance algorithms
lista.ForEach(item => DistanceAlgorithms.ApplyAlgorithms(item));
            
//Displaying the results
string salida = path + "\\train\\" + filename + ".out";
            
StreamWriter sw = new StreamWriter(salida, false);

lista.ForEach(item => sw.WriteLine(ManejadorCadena.BuildOutString(item, false).Replace(",", ".").Replace("|", ",")));
            
sw.Flush();
sw.Close();

Let's see the code of the algorithms for calculating distances.

The Jaro-Winkler distance code is not mine. I used it from stack overflow.

using System;

namespace es.jutrera.logistic
{
    public static class JaroWinklerDistance
    {
        /* The Winkler modification will not be applied unless the 
         * percent match was at or above the mWeightThreshold percent 
         * without the modification. 
         * Winkler's paper used a default value of 0.7
         */
        private static readonly double mWeightThreshold = 0.7;

        /* Size of the prefix to be concidered by the Winkler modification. 
         * Winkler's paper used a default value of 4
         */
        private static readonly int mNumChars = 4;

        /// <summary>
        /// Returns the Jaro-Winkler distance between the specified  
        /// strings. The distance is symmetric and will fall in the 
        /// range 0 (perfect match) to 1 (no match). 
        /// </summary>
        /// <param name="aString1">First String</param>
        /// <param name="aString2">Second String</param>
        /// <returns></returns>
        public static double distance(string aString1, string aString2)
        {
            return proximity(aString1, aString2);
        }

        /// <summary>
        /// Returns the Jaro-Winkler distance between the specified  
        /// strings. The distance is symmetric and will fall in the 
        /// range 0 (no match) to 1 (perfect match). 
        /// </summary>
        /// <param name="aString1">First String</param>
        /// <param name="aString2">Second String</param>
        /// <returns></returns>
        public static double proximity(string aString1, string aString2)
        {
            int lLen1 = aString1.Length;
            int lLen2 = aString2.Length;
            if (lLen1 == 0)
                return lLen2 == 0 ? 1.0 : 0.0;

            int lSearchRange = Math.Max(0, Math.Max(lLen1, lLen2) / 2 - 1);

            bool[] lMatched1 = new bool[lLen1];
            for (int i = 0; i < lMatched1.Length; i++)
            {
                lMatched1[i] = false;
            }
            bool[] lMatched2 = new bool[lLen2];
            for (int i = 0; i < lMatched2.Length; i++)
            {
                lMatched2[i] = false;
            }

            int lNumCommon = 0;
            for (int i = 0; i < lLen1; ++i)
            {
                int lStart = Math.Max(0, i - lSearchRange);
                int lEnd = Math.Min(i + lSearchRange + 1, lLen2);
                for (int j = lStart; j < lEnd; ++j)
                {
                    if (lMatched2[j]) continue;
                    if (aString1[i] != aString2[j])
                        continue;
                    lMatched1[i] = true;
                    lMatched2[j] = true;
                    ++lNumCommon;
                    break;
                }
            }
            if (lNumCommon == 0) return 0.0;

            int lNumHalfTransposed = 0;
            int k = 0;
            for (int i = 0; i < lLen1; ++i)
            {
                if (!lMatched1[i]) continue;
                while (!lMatched2[k]) ++k;
                if (aString1[i] != aString2[k])
                    ++lNumHalfTransposed;
                ++k;
            }
            
            int lNumTransposed = lNumHalfTransposed / 2;

            double lNumCommonD = lNumCommon;
            double lWeight = (lNumCommonD / lLen1
                             + lNumCommonD / lLen2
                             + (lNumCommon - lNumTransposed) / lNumCommonD) / 3.0;

            if (lWeight <= mWeightThreshold) return lWeight;
            int lMax = Math.Min(mNumChars, Math.Min(aString1.Length, aString2.Length));
            int lPos = 0;
            while (lPos < lMax && aString1[lPos] == aString2[lPos])
                ++lPos;
            if (lPos == 0) return lWeight;
            return lWeight + 0.1 * lPos * (1.0 - lWeight);

        }
    }
}

Here is the code for Levenshtein distance.

using System;

namespace es.jutrera.logistic
{
    public static class LevenshteinDistance
    {
        /// <summary>
        /// Applies the Levenshtein distance algorithm
        /// </summary>
        /// <param name="a">First String</param>
        /// <param name="b">Second String</param>
        /// <returns></returns>
        public static int Levenshtein(string a, string b)
        {
            int n = a.Length;
            int m = b.Length;

            // minimal change matrix
            int[][] d;
            d = new int[n][];
            for (int x = 0; x < d.Length; x++)
                d[x] = new int[m];

            if (n == 0)
                return m;
            if (m == 0)
                return n;

            // setup the worst case (insert all)
            for (int i = 0; i < n; i++)
                d[i][0] = i;
            for (var j = 0; j < m; j++)
                d[0][j] = j;

            // each matrix element will be the transition at lower cost
            for (int i = 1, I = 0; i < n; i++, I++)
                for (int j = 1, J = 0; j < m; j++, J++)
                    if (b[J] == a[I])
                        d[i][j] = d[I][J];
                    else
                    {
                        int aux = Math.Min(d[I][j], d[i][J]);
                        d[i][j] = Math.Min(aux, d[I][J]) + 1;
                    }
            // the lowest operation number
            return d[n - 1][m - 1];
        }
    }
}

After executing, we have this output file. We will use this data to train our machine.

train data source

Training the machine

Let's use the Octave application to perform logistic regression. We will use what I have learned in the Coursera's MOOC Machine Learning course (thanks Andrew NG!).

The train.m archive will do the work.

%% Initialization
clear ; close all; clc

%% Load Data
%  The first two columns contains the X and the thirteen column contains the label.

data = load('source.out');
X = data(:, [1:2]); y = data(:, 3);

%  Setup the data matrix 
[m, n] = size(X);
X = [ones(m, 1) X];

% Initialize fitting parameters
initial_theta = zeros(n + 1, 1);

%  Set options for fminunc
options = optimset('GradObj', 'on', 'MaxIter', 400);

%  Run fminunc to obtain the optimal theta
%  This function will return theta and the cost 
[theta, cost] = fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);

% Print theta to screen
fprintf('Cost at theta found by fminunc: %f\n', cost);
fprintf('theta: \n');
fprintf(' %f \n', theta);

% Plot Boundary
plotDecisionBoundary(theta, X, y);

% Put some labels 
hold on;
% Labels and Legend
xlabel('Levenshtein')
ylabel('Jaro-Winkler')

% Specified in plot order
legend('Same', 'Not same')
pause;
hold off;

fprintf('\nProgram paused. Press enter to continue.\n');
pause;

prob = sigmoid([1, 2, 0.8] * theta);
fprintf(['prediction probability (Lev: %f, J-W: %f): %f\n\n'], 2, 0.8, prob);

% Compute accuracy on our training set
p = predict(theta, X);

fprintf('Train Accuracy: %f\n', mean(double(p == y)) * 100);

fprintf('\nProgram paused. Press enter to continue.\n');
pause;

%train examples
error_data = load('cross.out');
X_cross = error_data(:, [1:2]); 
y_cross = error_data(:, 3);
[error_train, error_val] = learningCurve(X, y, [ones(size(X_cross, 1), 1) X_cross], y_cross, theta);

figure;
hold on;
plot(1:m, error_train);
plot(1:m, error_val, 'color',  'g');
title('Regression Learning Curve');
xlabel('Number of training examples')
ylabel('Error')
%axis([0 13 0 100])
legend('Train', 'Cross Validation')
pause;
hold off;
fprintf('Program paused. Press enter to continue.\n');
pause;

The result of executing this code is displayed in the next image

octave output display

The theta matrix has the gradient descent values for all the inputs. Let's see in the next chart. The + values represents when two strings are the same and Ø elsewhere.

data chart

The decision boundary seems right. If we make a prediction with two strings that have a value of 2.0 with Levenshtein and 0.8 of Jaro-Winkler, the probability of both string to be at least same (not a significant difference) is about 0.85. taking the decision boundary of Same if probability is greater or equal than 0.5 and Not same when this probability is less than 0.5, we can say that the two strings are not significally different.

Let's see the Cross validation chart

we can see that the error has a good value and the gap of the cross validation curve is right.

Final Conclusion

After this study, we have an algorithm that allows us to identify if there are significant changes between two strings. As we can see, provides a slightly more efficient tool that simply applying a strings distance algorithm. While the Jaro-Winkler algorithm is a bit more effective, once combined with Levenshtein and applied to training on a data set, we can see that the result fits best.

Other functions applied

I have been applied other hipothesis functions (lineal, cuadratic and cubic) to test how works. Results are right and can fit right (some fits better than the function I used). Here is the decission boundary charts of the three functions. CAn you guess them?