Intel®Developer Zone offers tools and how-to information for cross-platform app development, platform and technology information, code samples, and peer expertise to help developers innovate and succeed. Join our communities for the Internet of Things, Android*, Intel® RealSense™ Technology and Windows* to download tools, access dev kits, share ideas with like-minded developers, and participate in hackathons, contests, roadshows, and local events.
SPVR efficiently renders a large volume by breaking it into smaller pieces and processing only the occupied pieces. We call the pieces "metavoxels"; a voxel is the volume’s smallest piece. A metavoxel is a 3D array of voxels. And the overall volume is a 3D array of metavoxels. The sample has compile-time constants for defining these numbers. It’s currently configured for a total volume size of 10243 voxels, in the form of 323 metavoxels, each composed of 323 voxels.
The sample also achieves efficiency by populating the volume with volume primitives1. Many volume primitive types are possible. The sample implements one of them: a radially displaced sphere. The sample uses a cube map to represent the displacement over the sphere’s surface (see below for details). We identify the metavoxels affected by the volume primitives, compute the color and density of the affected voxels, propagate lighting, and ray-march the result from the eye’s point of view.
The sample also makes efficient use of memory. Consider the volume primitives as a compressed description of the volume’s contents. The algorithm effectively decompresses them on the fly, iterating between populating and ray-marching metavoxels. It can perform this switch for every metavoxel. But, switching between filling and ray marching has costs (e.g., changing shaders), so the algorithm supports filling a list of metavoxels before switching to ray-marching them. It allocates a relatively small array of metavoxels, reusing them as needed to process the total volume. Note also that many typical use cases occupy only a small percentage of the total volume in the first place.
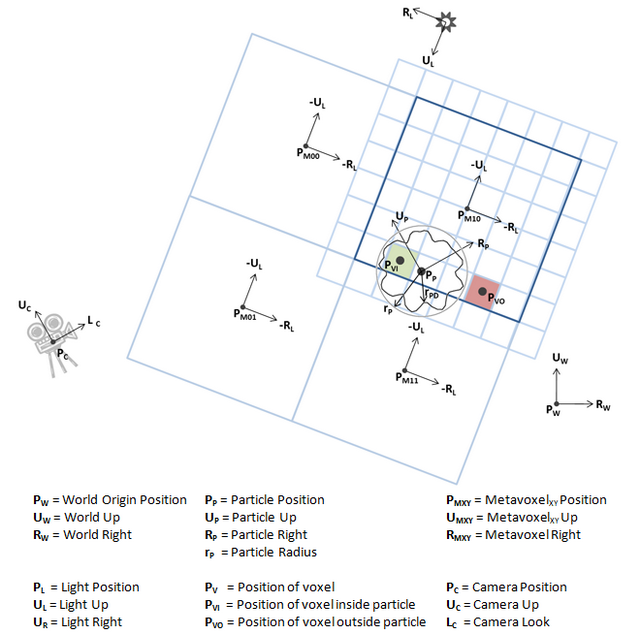
Figure 1. Particles, Voxels, Metavoxels, and the system’s various coordinate systems
Figure 1 shows some of the system’s participants: voxels, metavoxels, a volume-primitive particle, a light, a camera, and the world. Each has a reference frame, defined by a position P, an up vector U, and a right vector R. The real system is 3D, but Figure 1 is simplified to 2D for clarity.
- Voxel – The volume’s smallest piece. Each voxel stores a color and a density.
- Metavoxel – A 3D array of voxels. Each metavoxel is stored as a 3D texture (e.g., a 323
DXGI_FORMAT_R16G16B16A16_FLOAT 3D texture). - Volume – The overall volume is composed of multiple metavoxels. Figure 1 shows a simplified volume of 2x2 metavoxels.
- Particle – A radially displaced sphere volume primitive. Note, this is a 3D particle, not a 2D billboard.
- Camera – Same camera used for rendering the rest of the scene from the eye’s point of view.
Algorithm Overview
foreach scene model visible from light
draw model from light view
foreach scene model visible from eye
draw model from eye view
foreach particle
foreach metavoxel covered by the particle
append particle to metavoxel’s particle list
foreach non-empty metavoxel
fill metavoxel with binned particles and shadow map as input
ray march metavoxel from eye point of view, with depth buffer as input
foreach scene model
draw model from eye view
draw full-screen sprite with eye-view render target as texture
Note that the sample supports filling multiple metavoxels before ray-marching them. It fills a "cache" of metavoxels, then ray-marches them, repeating until it finishes processing all non-empty metavoxels. It also supports filling the metavoxels only every nth frame, or filling them only once. If the real app needs only a static or slowly changing volume, then it can be significantly faster by not updating the metavoxels every frame.
Filling the volume
The sample fills the metavoxels with the particles that cover them. "Covered" means the particles’ bounds intersect the metavoxel’s bounds. The sample avoids processing empty metavoxels. It stores color and density in each of the metavoxel’s voxels (color in RGB, and density in alpha). It performs this work in a pixel shader. It writes to the 3D texture as a RWTexture3D Unordered Access View (UAV). The sample draws a two-triangle 2D square, sized to match the metavoxel (e.g., 32x32 pixels for a 32x32x32 metavoxel). The pixel shader loops over each voxel in the corresponding voxel column, computing each voxel’s density and lit color from the particles that cover the metavoxel.
The sample determines if each voxel is inside each particle. The 2D diagram shows a simplified particle. (The diagram shows a radially displaced 2D circle. The 3D system implements radially displaced spheres.) Figure 1 shows the particle’s bounding radius rP and its displaced radius rPD. The particle covers the voxel if the distance between the particle’s center PP and the voxel’s center PV is less than the displaced distance rPD. For example: the voxel at PVI is inside the particle, while the voxel at PVO is outside.
Inside = |PV– PP| < rPD
The dot product inexpensively computes the square of a vector’s length, thus avoiding a relatively expensive sqrt() by comparing the squares of the lengths.
Inside = (PV– PP) ∙ (PV– PP) < rPD2
Color and density are functions of the voxel’s position within the particle and the distance to the particle’s surface rPD along the line from the particle’s center through the voxel’s center.
C = color(PV – PP, rPD)
D = density(PV – PP, rPD)
Different density functions are interesting. Here are some possibilities:
- Binary – If voxel is inside the particle, color=C and density=D (where C and D are constant). Otherwise color=BLACK and density=0.
- Gradient – Color varies from C1 to C2, and density varies from D1 to D2 as distance from the voxel’s position varies from the particle’s center to the particle’s surface.
- Texture Lookup – The color can be stored in a 1D, 2D, or 3D texture and looked up using distance, (X,Y,Z).
The sample implements two examples: 1) constant color, with ambient term given by the displacement value, and 2) gradient from bright yellow to black based on radius and particle age.
There are (at least) three interesting ways of specifying positions within a metavoxel.
- Normalized
- Float
- Origin at metavoxel center
- Range -1.0 to 1.0
- Texture Coordinates
- Float (converted to fixed-point by texture fetch machinery)
- Origin at top-left corner for 2D (top-left back for 3D)
- Range 0.0 to 1.0
- Voxel centers at 0.5/metavoxelDimensions (i.e., 0.0 is corner of voxel. 0.5 is center)
- Voxel Index
- Integer
- Origin at top-left corner for 2D (top-left back for 3D)
- Range 0 to metavoxelDimensions – 1
- Z is light direction, and X and Y are the plane perpendicular to the light direction
A voxel’s position in metavoxel space is given by the metavoxel’s position PM and voxel’s (X, Y) indices. The voxel indices are discrete, varying from 0 to N-1 across the metavoxel’s dimensions. Figure 1 shows a simplified 2x2 grid of 8x8-voxel metavoxels with PVI in metavoxel (1, 0) at voxel position (2, 6).
Lighting
After the sample computes color and density for each of the metavoxel’s voxels, it lights the voxels. The sample implements a simple lighting model. The pixel shader steps along the voxel column, multiplying the voxel’s color by the current light value. It then attenuates the light value according to the voxel’s density. There are (at least) two ways to attenuate the lighting. Wrenninge and Zafar1 use a factor of e-density. We use 1/(1+density). Both vary from 1 at 0 to 0 at infinity. The results look similar, but the divide can be faster than exp().
Ln+1 = Ln/(1+densityn)
Note that this loop propagates lighting through a single metavoxel. The sample propagates lighting from one metavoxel to the next via a light-propagation texture. It writes the last light-propagation value to the texture. The next metavoxel reads its initial light-propagation value from the texture. This 2D texture is sized for the entire volume. Sizing for the entire volume provides two benefits: it allows processing multiple metavoxels in parallel, and its final contents can be used as a light map for casting shadows from the volume onto the rest of the scene.
Shadows
The sample implements shadows cast from the scene onto the volume and shadows cast from the volume onto the scene. It first renders the scene’s opaque objects to a simple shadow map. The volume receives shadows by referencing the shadow map at the beginning of light propagation. It casts shadows by projecting the final light-propagation texture onto the scene. We cover a few more details about the light-propagation texture later in this document.
The shader samples the shadow map only once per metavoxel (per voxel column). The shader determines the index (i.e., row within the column) at which the first voxel falls in shadow. Voxels before shadowIndex aren’t in shadow. Voxels at or after shadowIndex are in shadow.

Figure 2. Relationship between shadow Z values and indices
The shadowIndex varies from 0 to METAVOXEL_WIDTH as the shadow value varies from the top of the metavoxel to the bottom. Metavoxel local space is centered at (0, 0, 0) and ranges from -1.0 to 1.0. So, the top is at (0, 0, -1), and the bottom is at (0, 0, 1). Transforming to light/shadow space gives:
Top = (LightWorldViewProjection._m23 - LightWorldViewProjection._m22)
Bottom = (LightWorldViewProjection._m23 + LightWorldViewProjection._m22)
Resulting in the following shader code in FillVolumePixelShader.fx:
float shadowZ = _Shadow.Sample(ShadowSampler, lightUv.xy).r;
float startShadowZ = LightWorldViewProjection._m23 - LightWorldViewProjection._m22;
float endShadowZ = LightWorldViewProjection._m23 + LightWorldViewProjection._m22;
uint shadowIndex = METAVOXEL_WIDTH*(shadowZ-startShadowZ)/(endShadowZ-startShadowZ);
Note that the metavoxels are cubes, so METAVOXEL_WIDTH is also the height and depth.
Light-propagation texture
In addition to computing each voxel’s color and density, FillVolumePixelShader.fx writes the final propagated light value to a light-propagation texture. The sample refers to this texture by the name "$PropagateLighting". It’s a 2D texture, covering the whole volume. For example, the sample, as configured for a 10243 volume (323 metavoxels, each with 323 voxels), would have a 1024x1024 (32*32=1024) light-propagation texture. There are two twists: this texture includes space for each metavoxel’s one-voxel border, and the value stored in the texture is the last non-shadowed value.
Each metavoxel maintains a one-voxel border so texture filtering works (when sampling during the eye-view ray march). The sample casts shadows from the volume onto the rest of the scene by projecting the light-propagation texture onto the scene. A simple projection would show visual artifacts where the texture duplicates values to support the one-voxel border. It avoids these artifacts by adjusting the texture coordinates to accommodate the one-voxel border. Here’s the code (from DefaultShader.fx):
float oneVoxelBorderAdjust = ((float)(METAVOXEL_WIDTH-2)/(float)METAVOXEL_WIDTH);
float2 uvVol = input.VolumeUv.xy * 0.5f + 0.5f;
float2 uvMetavoxel = uvVol * WIDTH_IN_METAVOXELS;
int2 uvInt = int2(uvMetavoxel);
float2 uvOffset = uvMetavoxel - (float2)uvInt - 0.5f;
float2 lightPropagationUv = ((float2)uvInt + 0.5f + uvOffset * oneVoxelBorderAdjust )
* (1.0f/(float)WIDTH_IN_METAVOXELS);
The light-propagation texture stores the light value at the last voxel that isn’t in shadow. Once the light propagation process encounters the shadowing surface, the propagated lighting goes to 0 (no light propagates past the shadow caster). But, storing the last light value allows us to use the texture as a light map. Projecting this last-lighting value onto the scene means the shadow casting surface receives the expected lighting value. Surfaces that are in shadow effectively ignore this texture.
Ray Marching

Figure 3. Eye-View Ray March
The sample ray-marches the metavoxel with a pixel shader (EyeViewRayMarch.fx), sampling from the 3D texture as a Shader Resource View (SRV). It marches each ray from far to near with respect to the eye. It performs filtered samples from the metavoxel’s corresponding 3D texture. Each sampled color adds to the final color, while each sampled density occludes the final color and the final alpha.
blend = 1/(1+density)
colorresult = colorresult * blend + color * (1-blend)
alpharesult = alpharesult * blend
The sample processes each metavoxel independently. It ray-marches each metavoxel one at a time, blending the results with the eye-view render target to generate the combined result. It marches each metavoxel by drawing a cube (i.e., 12 triangles) from the eye’s point of view. The pixel shader marches a ray through each pixel covered by the cube. It renders the cube with front-face culling so the pixel shader executes only once for each covered pixel. If it rendered without culling, then each ray could be marched twice—once for the front faces and once for the back faces. If it rendered with back-face culling, then when the camera is inside the cube, the pixels would be culled, and the rays wouldn’t be marched.
The simple example in Figure 3 shows two rays marched through four metavoxels. It illustrates how the ray steps are distributed along each ray. The distance between the steps is the same when projected onto the look vector. That means the steps are longer for off-axis rays. This approach empirically yielded the best-looking results (versus, for example, equal steps for all rays). Note the sampling points all start on the far plane and not on the metavoxel’s back surface. This matches how they would be sampled for a monolithic volume, without the concept of metavoxels. Starting the ray march on each metavoxel’s back surface resulted in visible seams at metavoxel boundaries.
Figure 3 also shows how the samples land in the different metavoxels. The gray samples are outside all metavoxels. The red, green, and blue samples land in separate metavoxels.
Depth test
The ray-march shader honors the depth buffer by truncating the rays against the depth buffer. It does this efficiently by beginning the ray march at the first ray step that would pass the depth test.

Figure 4. Relationship between depths and indices
The relationship between depth values and ray-march indices is shown in Figure 4. It reads the Z value from the Z buffer and computes the corresponding depth value (i.e., distance from the eye). The indices vary proportionally from 0 to totalRaymarchCount as the depth varies from zMin to zMax. Resulting in this code (from EyeViewRayMarch.fx):
float depthBuffer = DepthBuffer.Sample( SAMPLER0, screenPosUV ).r;
float div = Near/(Near-Far);
float depth = (Far*div)/(div-depthBuffer);
uint indexAtDepth = uint(totalRaymarchCount * (depth-zMax)/(zMin-zMax));
Where zMin and zMax are the depth values at the ray-march extents. zMax and zMin are the values at the furthest point from the eye, and closest point, respectively.
Sorting
Metavoxel rendering honors two sort orders: one for the light and one for the eye. Light propagation starts at the metavoxels closest to the light and progresses through more distant metavoxels. The metavoxels are semi-transparent, so correct results also require sorting from the eye view. The two choices when sorting from the eye view are: back to front with "over" alpha blending and front to back with "under" alpha blending.

Figure 5. Metavoxel sort order
Figure 5 shows a simple arrangement of three metavoxels, a camera for the eye, and a light. Light propagation requires an order of 1, 2, 3; we must propagate the lighting through metavoxel 1 to know how much light makes it to metavoxel 2. And, we must propagate light through metavoxel 2 to know how much light makes it to metavoxel 3.
We also need to sort the metavoxels from the eye’s point of view. If rendering front to back, we would render metavoxel 2 first. The blue and purple lines show how metavoxels 1 and 3 are behind metavoxel 2. We need to propagate lighting through metavoxels 1 and 2 before we can render metavoxel 3. The worst case requires propagating lighting through the entire column before rendering any of them. Rendering that case back-to-front allows us to render each metavoxel immediately after propagating its lighting.
The sample combines both back-to-front and front-to-back sorting to support the ability to render metavoxels immediately after propagating lighting. The sample renders metavoxels above the perpendicular (i.e., the green line) back-to-front with over-blending, followed by the metavoxels below the perpendicular front-to-back with under-blending. This ordering produces the correct results without requiring enough memory to hold an entire column of metavoxels. Note that the algorithm could always sort front-to-back with under-blending if the app can commit enough memory.
Alpha Blending
The sample uses over-blending for the metavoxels that are sorted back-to-front (i.e., the most-distant metavoxel is rendered first, followed by successively closer metavoxels). It uses under-blending for the metavoxels that are sorted front-to-back (i.e., the closest metavoxel is rendered first, with more-distant metavoxels rendered behind).
Over-blend: Colordest = Colordest * Alphasrc + Colorsrc
Under-blend: Colordest = Colorsrc * Alphadest + Colordest
The sample blends the alpha channel the same for both over- and under-blending; they both simply scale the destination alpha by the pixel shader alpha.
Alphadest = Alphadest * Alphasrc
The following are the render states used for over- and under-blending.
Over-Blend Render States (From EyeViewRayMarchOver.rs)
SrcBlend = D3D11_BLEND_ONE
DestBlend = D3D11_BLEND_SRC_ALPHA
BlendOp = D3D11_BLEND_OP_ADD
SrcBlendAlpha = D3D11_BLEND_ZERO
DestBlendAlpha = D3D11_BLEND_SRC_ALPHA
BlendOpAlpha = D3D11_BLEND_OP_ADD
Under-Blend Render States (From EyeViewRayMarchUnder.rs)
SrcBlend = D3D11_BLEND_DEST_ALPHA
DestBlend = D3D11_BLEND_ONE
BlendOp = D3D11_BLEND_OP_ADD
SrcBlendAlpha = D3D11_BLEND_ZERO
DestBlendAlpha = D3D11_BLEND_SRC_ALPHA
BlendOpAlpha = D3D11_BLEND_OP_ADD
Compositing
The result of the eye-view ray march is a texture with a pre-multiplied alpha channel. We draw a full screen sprite with alpha blending enabled to composite with the back buffer.
Colordest = Colordest * Alphasrc + Colorsrc
The render states are:
SrcBlend = D3D11_BLEND_ONE
DestBlend = D3D11_BLEND_SRC_ALPHA
The sample supports having an eye-view render target with a different resolution from the back buffer. A smaller render target can significantly improve performance as it reduces the total number of rays marched. However, when the render target is smaller than the back buffer, the composite step performs up-sampling that can generate cracks around silhouette edges. This common issue, left for future work, can be addressed by up-sampling during the compositing step.
Known Issues
- If the eye-view render target is smaller than the back buffer, cracks appear when compositing.
- Resolution-mismatch between the light-propagation texture and the shadow map results in cracks.
Conclusion
The sample efficiently renders volumetric effects by filling a sparse volume with volume primitives and ray-marching the result from the eye. It’s a proof of concept, illustrating end-to-end support for integrating volumetric effects with existing scenes.
Misc
View some SPVR slides from the SIGGRAPH 2014 presentation:
https://software.intel.com/sites/default/files/managed/64/3b/VolumeRendering.25.pdf
See the sample in action on Youtube*:
http://www.youtube.com/watch?v=50GEvbOGUks
http://www.youtube.com/watch?v=cEHY9nVD23o
http://www.youtube.com/watch?v=5yKBukDhH80
http://www.youtube.com/watch?v=SKSPZFM2G60
Learn more about optimizing for Intel platforms:
Whitepaper: Compute Architecture of Intel Processor Graphics Gen 8
IDF Presentation: Compute Architecture of Intel Processor Graphics Gen 8
Whitepaper: Compute Architecture of Intel Processor Graphics Gen 7.5
Intel Processor Graphics Public Developer Guides & Architecture Docs (Multiple Generations)
Acknowledgement
Many thanks to the following for their contributions: Marc Fauconneau-Dufresne, Tomer Bar on, Jon Kennedy, Jefferson Montgomery, Randall Rauwendaal, Mike Burrows, Phil Taylor, Aaron Coday, Egor Yusov, Filip Strugar, Raja Bala, and Quentin Froemke.
References
1. M. Wrenninge and N. B. Zafar, SIGGRAPH 2010 and 2011 Production Volume Rendering course notes: http://magnuswrenninge.com/content/pubs/ProductionVolumeRenderingFundamentals2011.pdf
2. M. Ikits, J. Kniss, A. Lefohn, and C. Hansen, Volume Rendering Techniques, GPU Gems, http://http.developer.nvidia.com/GPUGems/gpugems_ch39.html
